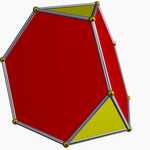
Triakisni tetraeder

Triakisni tetraeder
(animacija)
Vrsta	Catalanovo telo
Coxeter-Dinkinov diagram
Vrsta stranskih ploskev	enakostranični trikotniki
Stranske ploskve	12
Robovi	18
Oglišča	8
Vrsta oglišč	4{3}+4{6}
Konfiguracija stranskih ploskev	V3.6.6
Simetrijska grupa	Td, A3, [3,3]+, *332
Vrtilna grupa	T, [3,3]+, 332
Diedrski kot	129º 31′ 16″ ${\displaystyle \arccos(-7/11)}$
Značilnosti	konveksen ploskovno prehoden
prisekani tetraeder (dualni polieder)	mreža telesa

Triakisni tetraeder (tudi kistetraeder^[1]) je dualno telo arhimedskega telesa ali Catalanovo telo. Njegov dual je prisekani tetraeder.

Lahko se ga obravnava tudi kot tetraeder, ki so se mu dodale tristrane piramide na vsako stransko ploskev. To pomeni, da je klitop (imenuje se po matematiku Victorju LaRueu Kleeju (1925–2007) tetraedra.

Če ima triakisni tetraeder krajši rob z dolžino 1, potem je njegova površina enaka ${\displaystyle {\tfrac {5}{3}}\scriptstyle {\sqrt {11}}}$ in prostornina ${\displaystyle {\tfrac {25}{36}}\scriptstyle {\sqrt {2}}}$

Triakisni tetraeder je del zaporedja poliedrov in tlakovanj, ki se jih lahko razširi tudi v hiperbolično ravnino. Te oblike s prehodnimi stranskimi ploskvami imajo zrcalno simetrijo (*n32).

Simetrija	Sferna				Ravninska	Hiperbolična...
	*232 [2,3] D3h	*332 [3,3] Td	*432 [4,3] Oh	*532 [5,3] Ih	*632 [6,3] P6m	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Red	12	24	48	120	∞
Prisekane oblike	3.4.4	3.6.6	3.8.8	3.10.10	3.12.12	3.14.14	3.16.16	3.∞.∞
Coxeter Schläfli	t0,1{2,3}	t0,1{3,3}	t0,1{4,3}	t0,1{5,3}	t0,1{6,3}	t0,1{7,3}	t0,1{8,3}	t0,1{∞,3}
Triakisne oblike	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14
Coxeter

• prisekani triakisni tetraeder

• Conway, John Horton; Burgiel, Heidi; Goodman-Strass, Chaim (2008), »§21, Naming the Archimedean and Catalan polyhedra and tilings«, The Symmetries of Things, str. 284, COBISS 29751813, ISBN 978-1-56881-220-5

• Weisstein, Eric Wolfgang. »TriakisTetrahedron«. MathWorld.