Trapezoedru hexagonal
| Trapezoedru hexagonal | |
 | |
| Descriere | |
|---|---|
| Tip | trapezoedru |
| Fețe | 12 romboizi |
| Laturi (muchii) | 24 |
| Vârfuri | 14 |
| χ | 2 |
| Configurația feței | V6.3.3.3 |
| Simbol Schläfli | { } ⨁ {6}[1] |
| Simbol Conway | dA6[2] |
| Diagramă Coxeter | |
| Grup de simetrie | D6d, [2+,12], (2*6), ordin 24 |
| Grup de rotație | D6, [2,6]+, (226), ordin 12 |
| Volum | ≈ 19,697 a3 (a = latura mică) |
| Poliedru dual | antiprismă hexagonală |
| Proprietăți | convex, cu fețe romboidale, tranzitiv pe fețe |
În geometrie un trapezoedru hexagonal este un romboedru (un poliedru tridimensional cu fețe în formă de romboizi) în care, în plus, toate fețele sunt congruente. Având 12 fețe, este un dodecaedru neregulat. Este tranzitiv pe fețe și poate fi descris prin simbolul Conway dA6.[2]
Este al patrulea dintr-o serie infinită de trapezoedre care sunt dualele antiprismelor, fiind dualul antiprismei hexagonale.
Simetrie
[modificare | modificare sursă]Grupul de simetrie al trapezoedrului hexagonal este D6d de ordinul 24. grupul de rotație este D6 de ordinul 12.
Variații
[modificare | modificare sursă]Un grad de libertate în simetria D6 transformă romboizii în patrulatere congruente cu laturi de 3 lungimi diferite. La limită, o latură a fiecărui patrulater ajunge la lungimea zero, iar trapezoedrul devine o bipiramidă.
Aranjamentele cristaline ale atomilor se pot repeta în spațiu cu o configurație trapezoedrică hexagonală în jurul unui atom, care este întotdeauna enantiomorf,[3] și cuprinde grupurile spațiale(d) 177–182.[4] β-cuarțul este singurul mineral comun cu acest sistem cristalin.[5]
Dacă romboizii care înconjoară cele două vârfuri sunt de forme diferite, acesta poate avea doar simetrie C6v, de ordinul 12. Acestea pot fi numite trapezoedre inegale. Dualul este o antiprismă inegală, cu poligoanele de sus diferite de cele de jos. Dacă este răsucit și inegal, simetria sa se reduce la o simetrie ciclică, simetria C6, de ordinul 6.
| Tip | Trapezoedru răsucit (izoedric) | Trapezoedru inegal | Inegal și răsucit | |
|---|---|---|---|---|
| Simetrie | D6, (662), [6,2]+, ordin 12 | C6v, (*66), [6], ordin 12 | C6, (66), [6]+, ordin 6 | |
| Imagine (n = 6) |

|

|

|

|
| Desfășurată | 
|

|

|

|
Mărimi asociate
[modificare | modificare sursă]Unghi diedru
[modificare | modificare sursă]Unghiul diedru al unui trapezoedru hexagonal regulat cu toate unghiurile diedre egale este:[6]
Dacă z este latura poliedrului dual (antiprisma hexagonală), atunci mărimile asociate sunt date de relațiile următoare:
Lungimile laturilor
[modificare | modificare sursă]Latura scurtă, a, are lungimea:[6]
Latura lungă, b, are lungimea:[6]
Volum
[modificare | modificare sursă]Volumul este:[6]
Poliedre înrudite
[modificare | modificare sursă]Poliedru dual
[modificare | modificare sursă]Dualul trapezoedrului hexagonal este antiprisma hexagonală.
Pavare sferică
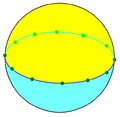
[modificare | modificare sursă]Trapezoedrul hexagonal există și ca pavare sferică, cu 2 vârfuri la poli și vârfuri alternante la distanță egală deasupra și sub ecuator.
| Poliedre sferice diedrice hexagonale uniforme | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
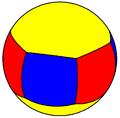
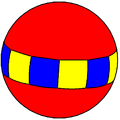
| Simetrie: [6,2], (*622) | [6,2]+, (622) | [6,2+], (2*3) | ||||||||||||

|
|

|

|

|
|
|

|

| ||||||
| {6,2} | t{6,2} | r{6,2} | t{2,6} | {2,6} | rr{6,2} | tr{6,2} | sr{6,2} | s{2,6} | ||||||
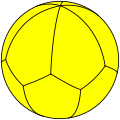
| Dualele celor de mai sus | ||||||||||||||

|

|

|

|

|

|

|
|

| ||||||
| V62 | V122 | V62 | V4.4.6 | V26 | V4.4.6 | V4.4.12 | V3.3.3.6 | V3.3.3.3 | ||||||
Note
[modificare | modificare sursă]- ^ en Norman Johnson, Geometries and Transformations, (2018) ISBN: 978-1-107-10340-5 Chapter 11: Finite symmetry groups, 11.3 Pyramids, Prisms, and Antiprisms, Figure 11.3c
- ^ a b C100dA6, polyHédronisme v0.2.1, accesat 2024-04-17
- ^ en 3 2 and Hexagonal-trapezohedric Class, 6 2 2
- ^ en Hahn, Theo, ed. (). International tables for crystallography (ed. 5th). Dordrecht, Netherlands: Published for the International Union of Crystallography by Springer. ISBN 978-0-7923-6590-7.
- ^ en „Crystallography: The Hexagonal System”. www.mindat.org. Accesat în .
- ^ a b c d en David McCooey, Hexagonal Trapezohedron, dmccooey.com, accesat 2024-04-21
Legături externe
[modificare | modificare sursă]- en Eric W. Weisstein, Trapezohedron la MathWorld.
- en Virtual Reality Polyhedra The Encyclopedia of Polyhedra
| Nume trapezoedru | Trapezoedru digonal (tetraedru) |
Trapezoedru trigonal |
Trapezoedru tetragonal |
Trapezoedru pentagonal |
Trapezoedru hexagonal |
Trapezoedru heptagonal |
Trapezoedru octogonal |
Trapezoedru decagonal |
Trapezoedru dodecagonal |
... | Trapezoedru apeirogonal |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Imagine | 
|
|

|

|

|

|

|

|
... | ||
| Pavare sferică |

|

|

|

|

|

|

|

|

|
Pavare plană |
|
| Configurația feței |
V2.3.3.3 | V3.3.3.3 | V4.3.3.3 | V5.3.3.3 | V6.3.3.3 | V7.3.3.3 | V8.3.3.3 | V10.3.3.3 | V12.3.3.3 | ... | V∞.3.3.3 |

