Figură izoedrică
În geometrie, un politop tridimensional (un poliedru) sau mai mare este izoedru sau tranzitiv pe fețe atunci când fețele sunt aceleași. Mai precis, toate fețele nu trebuie să fie doar congruente, ci trebuie să fie tranzitive, adică trebuie să se afle în aceeași orbită de simetrie. Cu alte cuvinte, pentru orice fețe A și B, trebuie să existe o simetrie a întregului poliedru prin rotații și reflexii care aplică A pe B. Din acest motiv, poliedrele izoedrice convexe sunt formele potrivite pentru zaruri corecte.[1]
Poliedrele izoedrice se numesc izoedre. Ele pot fi descrise prin configurația feței. O formă care este izoedrică și are vârfuri regulate este, de asemenea, tranzitivă pe muchii (izotoxală) și se spune că este un poliedru cvasiregulat dual: unii teoreticieni consideră aceste figuri ca fiind cu adevărat cvasiregulate, deoarece au aceleași simetrii, dar acest lucru nu este acceptat în general. Un izoedru are un număr par de fețe.[2]
Un poliedru care este izoedric are un poliedru dual care este tranzitiv pe vârfuri (izogonal). Poliedrele Catalan, bipiramidele și trapezoedrele sunt toate izoedrice. Acestea sunt duale ale poliedrelor izogonale: arhimedice, prisme și antiprisme. Poliedrele platonice, care sunt fie autoduale, fie dual al altui poliedru platonic, sunt tranzitive pe vârfuri, muchii și fețe (sunt izogonale, izotoxale și izoedrice). Se spune că un poliedru izoedric și izogonal este un poliedru nobil.
Nu toate izozonoedrele[3] sunt izoedrice.[4] De exemplu un icosaedru rombic este un izozonoedru, dar nu un izoedru.[5]
Exemple
[modificare | modificare sursă]| Convex | Concav | ||
|---|---|---|---|
 Bipiramida hexagonală, V4.4.6, nu este un poliedru regulat, dar este izoedrică. |
 Pavarea pentagonală Cairo, V3.3.4.3.4, este izoedrică. |
 Fagurele dodecaedric rombic este un fagure izoedric (și izotopic). |
 Pavarea topologic pătrată deformată în forme spirale H. |
Clasele izoedrelor după simetrie
[modificare | modificare sursă]| Fețe | Config. feței |
Clasă | Nume | Simetrie | Ordin | Convex | Coplanar | Neconvex |
|---|---|---|---|---|---|---|---|---|
| 4 | V33 | platonic | tetraedru, bisfenoid tetragonal, bisfenoid rombic |
Td, [3,3], (*332) D2d, [2+,2], (2*) D2, [2,2]+, (222) |
24 4 4 4 |
   |
||
| 6 | V34 | platonic | cub, trapezoedru trigonal, trapezoedru trigonal asimetric |
Oh, [4,3], (*432) D3d, [2+,6] (2*3) D3 [2,3]+, (223) |
48 12 12 6 |
   |
||
| 8 | V43 | platonic | octaedru, bipiramidă pătrată, bipiramidă rombică, scalenoedru pătrat |
Oh, [4,3], (*432) D4h,[2,4],(*224) D2h,[2,2],(*222) D2d,[2+,4],(2*2) |
48 16 8 8 |
      |
| |
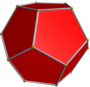
| 12 | V35 | platonic | dodecaedru regulat, piritoedru, tetartoid |
Ih, [5,3], (*532) Th, [3+,4], (3*2) T, [3,3]+, (*332) |
120 24 12 |
   |
  |
 
|
| 20 | V53 | platonic | icosaedru regulat | Ih, [5,3], (*532) | 120 |  |
||
| 12 | V3.62 | Catalan | tetraedru triakis | Td, [3,3], (*332) | 24 |  |
  |
|
| 12 | V(3.4)2 | Catalan | dodecaedru rombic, dodecaedru romboidal |
Oh, [4,3], (*432) Td, [3,3], (*332) |
48 24 |
   |
 |
 
|
| 24 | V3.82 | Catalan | octaedru triakis | Oh, [4,3], (*432) | 48 |  |
 
| |
| 24 | V4.62 | Catalan | hexaedru tetrakis | Oh, [4,3], (*432) | 48 |   |
  |
 
|
| 24 | V3.43 | Catalan | icositetraedru romboidal | Oh, [4,3], (*432) | 48 |   |
   |
|
| 48 | V4.6.8 | Catalan | dodecaedru disdiakis | Oh, [4,3], (*432) | 48 |  |
   |
 
|
| 24 | V34.4 | Catalan | icositetraedru pentagonal | O, [4,3]+, (432) | 24 |  |
||
| 30 | V(3.5)2 | Catalan | triacontaedru rombic | Ih, [5,3], (*532) | 120 |  |
||
| 60 | V3.102 | Catalan | icosaedru triakis | Ih, [5,3], (*532) | 120 |  |
   
| |
| 60 | V5.62 | Catalan | dodecaedru pentakis | Ih, [5,3], (*532) | 120 |  |
    
| |
| 60 | V3.4.5.4 | Catalan | hexacontaedru romboidal | Ih, [5,3], (*532) | 120 |  |
 |
|
| 120 | V4.6.10 | Catalan | triacontaedru disdiakis | Ih, [5,3], (*532) | 120 |  |
   |
  
|
| 60 | V34.5 | Catalan | hexacontaedru pentagonal | I, [5,3]+, (532) | 60 |  |
||
| 2n | V33.n | Polar | trapezoedru, trapezoedru asimetric |
Dnd, [2+,2n], (2*n) Dn, [2,n]+, (22n) |
4n 2n |
    |
||
| 2n 4n |
V42.n V42.2n V42.2n |
Polar | n-bipiramidă regulată, 2n-bipiramidă izotoxală, 2n-scalenoedru |
Dnh, [2,n], (*22n) Dnh, [2,n], (*22n) Dnd, [2+,2n], (2*n) |
4n |    |
      
|
Figuri k-izoedrice
[modificare | modificare sursă]Un poliedru (sau politop în general) este un k- izoedru dacă conține k fețe în domeniul său fundamental de simetrie.[6]
Similar, o k-pavare izoedrică are k orbite de simetrie separate (și poate conține m fețe de diferite forme pentru unele m < k ).[7]
Un poliedru monoedric sau pavare monoedrică (m = 1) are fețe congruente, direct sau reflexiv, care apar în una sau mai multe poziții de simetrie. Un poliedru sau pavare r-edrice are r tipuri de fețe (numite și diedrice pentru 2, respectiv triedrice pentru 3).[8]
Iată câteva exemple de poliedre și pavări k-izoedrice, cu fețele lor colorate în funcție de pozițiile lor de k-simetrie:
| 3-izoedric | 4-izoedric | Izoedric | 2-izoedric |
|---|---|---|---|
| Poliedre (2-edrice) cu fețe regulate | Poliedre monoedrice | ||
|
|
|
|
| Rombicuboctaedrul are 1 tip de triunghiuri și 2 tipuri de pătrate |
Pseudorombicuboctaedrul are 1 tip de triunghiuri și 3 tipuri de pătrate |
Icositetraedrul romboidal are 1 tip de față |
Icositetraedrul pseudoromboidal are 2 tipuri de fețe cu forme identice |
| 3-izoedric | 4-izoedric | Izoedric | 2-izoedric |
|---|---|---|---|
| Pavare regulată pe fețe (2-edrică) | Pavări monoedrice | ||
|
|
|
 |
| Pavare pitagoreică cu 2 dimensiuni de pătrate |
Pavare 3-uniformă cu 3 tipuri de triunghiuri și 1 pătrat |
Model schelet de pește cu 1 tip de dale (fețe) dreptunghiulare |
Pavare pentagonală cu 3 tipuri de dale (fețe) neregulate pentagonale |
Termeni asociați
[modificare | modificare sursă]O figură tranzitivă pe fațete sau izotopică este un politop sau fagure n-dimensionali cu fațete ((n−1)-fețe) congruente și tranzitive. Politopul dual al unui izotop este un politop izogonal. Prin definiție, această proprietate izotopică este comună dualelor politopurilor uniforme.
- O figură izotopică 1-dimensională este izogonală (tranzitivă pe vârfuri).
- O figură izotopică 2-dimensională este izotoxală (tranzitivă pe muchii).
- O figură izotopică 3-dimensională este izoedrică (tranzitivă pe fețe).
- O figură izotopică n-dimensională (n > 3) este izotopică (tranzitivă pe (n−1)-fețe). Pentru n = 4, izotopică înseamnă tranzitivă pe celule.
Note
[modificare | modificare sursă]- ^ en McLean, K. Robin (), „Dungeons, dragons, and dice”, The Mathematical Gazette, 74 (469): 243–256, doi:10.2307/3619822, JSTOR 3619822.
- ^ en Grünbaum (1960)
- ^ en Weisstein, Eric W. „Isozonohedron”. mathworld.wolfram.com (în engleză). Accesat în .
- ^ en Weisstein, Eric W. „Isohedron”. mathworld.wolfram.com (în engleză). Accesat în .
- ^ en Weisstein, Eric W. „Rhombic Icosahedron”. mathworld.wolfram.com (în engleză). Accesat în .
- ^ en
Socolar, Joshua E. S. (). „Hexagonal Parquet Tilings: k-Isohedral Monotiles with Arbitrarily Large k” (PDF). The Mathematical Intelligencer. 29: 33–38. arXiv:0708.2663
. doi:10.1007/bf02986203. Arhivat din original (corrected PDF) la . Accesat în .
- ^ en Craig S. Kaplan. "Introductory Tiling Theory for Computer Graphics". 2009. Chapter 5 "Isohedral Tilings". p. 35.
- ^ en Tilings and Patterns, p.20, 23
Bibliografie
[modificare | modificare sursă]- en Peter R. Cromwell, Polyhedra, Cambridge University Press 1997, ISBN: 0-521-55432-2, p. 367 Transitivity
Legături externe
[modificare | modificare sursă]- en Eric W. Weisstein, Isohedral tiling la MathWorld.
- en Eric W. Weisstein, Isohedron la MathWorld.
- en isohedra 25 de clase de izoedre cu un număr finit de muchii
- Dice Design at The Dice Lab
