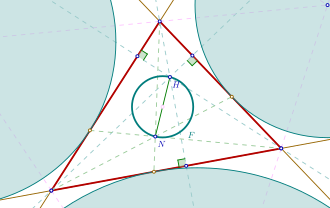
푸르만 원

기하학에서, 푸르만 원(영어: Fuhrmann circle)은 삼각형의 수심과 나겔 점을 잇는 선분을 지름으로 하는 원이다.

정의

삼각형 $ABC$ 의 외접원의 호 $BC$ , $CA$ , $AB$ 의 중점을 각각 $F_{A}'$ , $F_{B}'$ , $F_{C}'$ 라고 하자. 직선 $BC$ 에 대한 $F_{A}'$ 의 반사상을 $F_{A}$ , 직선 $CA$ 에 대한 $F_{B}'$ 의 반사상을 $F_{B}$ , 직선 $AB$ 에 대한 $F_{C}'$ 의 반사상을 $F_{C}$ 라고 하자. 그렇다면 삼각형 $F_{A}F_{B}F_{C}$ 를 원래 삼각형 $ABC$ 의 푸르만 삼각형(영어: Fuhrmann triangle)이라고 한다. 푸르만 삼각형의 외접원을 푸르만 원이라고 한다.

성질

푸르만 원은 수심과 나겔 점을 잇는 선분을 지름으로 한다.^[1]^{:50, §6} 특히, 푸르만 원의 중심은 수심과 나겔 점을 잇는 선분의 중점이다.

증명:

삼각형 $ABC$ 의 수심을 $H$ , 나겔 점을 $X_{8}$ 이라고 하자. 그렇다면 $F_{A}F_{A}'$ 은 선분 $BC$ 의 수직 이등분선이므로, 선분 $BC$ 의 중점 $M_{A}$ 와 외심 $O$ 를 지난다. 특히 $O$ 에 대한 $F_{A}'$ 의 반사상을 $F_{A}''$ 이라고 할 경우 선분 $F_{A}'F_{A}''$ 은 외접원의 지름이다. $AH$ 와 $F_{A}''F_{A}$ 는 모두 $BC$ 의 수선이므로 평행한다. 또한

{\begin{aligned}AH&=2OM_{A}\\&=2OF_{A}'-2M_{A}F_{A}'\\&=F_{A}''F_{A}'-F_{A}F_{A}'\\&=F_{A}''F_{A}\end{aligned}}

이므로 선분 $HF_{A}$ 는 선분 $AF_{A}''$ 의 평행 이동상이며, 특히 이 두 선분의 직선은 평행한다.

삼각형 $ABC$ 의 반중점 삼각형 $A'B'C'$ 의 $A$ , $B$ , $C$ 에 대한 꼭짓점을 $A'$ , $B'$ , $C'$ 이라고 하자. 그렇다면 $X_{8}$ 은 삼각형 $A'B'C'$ 의 내심이며, 특히 $A'X_{8}$ 은 삼각형 $A'B'C'$ 의 내각 이등분선이다. $AF_{A}'$ 역시 삼각형 $ABC$ 의 내각 이등분선이므로, $A'X_{8}$ 과 $AF_{A}'$ 은 평행한다. $M_{A}$ 는 선분 $AA'$ 과 $F_{A}F_{A}'$ 의 공통 중점이므로, 선분 $AF_{A}'$ 과 $A'F_{A}$ 는 서로 $M_{A}$ 에 대한 반사상이며, 특히 이 두 선분의 직선은 평행한다. 따라서, $A'$ , $X_{8}$ , $F_{A}$ 는 공선점이며, $X_{8}F_{A}$ 와 $AF_{A}'$ 은 평행한다.

선분 $F_{A}'F_{A}''$ 은 삼각형 $ABC$ 의 외접원의 지름이므로, $AF_{A}'$ 과 $AF_{A}''$ 은 서로 수직이다. 따라서 $X_{8}F_{A}$ 와 $HF_{A}$ 역시 서로 수직이며, $F_{A}$ 는 선분 $HX_{8}$ 를 지름으로 하는 원 위의 점이다.

삼각형 $ABC$ 의 세 변의 길이를 $a=BC$ , $b=AC$ , $c=AB$ 라고 하고, 외접원의 반지름을 $R$ 라고 하자. 그렇다면 푸르만 원의 반지름은

R{\sqrt {\frac {a^{3}+b^{3}+c^{3}-(a^{2}b+a^{2}c+ab^{2}+b^{2}c+ac^{2}+bc^{2})+3abc}{abc}}}

이다.^[2]^{:148, §11.17}

삼각형 $ABC$ 의 내접원의 반지름을 $r$ 라고 하고, 각 꼭짓점 $A$ , $B$ , $C$ 에서 대변에 내린 수선과 푸르만 원 사이의 수심이 아닌 교점을 $P$ , $Q$ , $R$ 라고 하자. 그렇다면

AP=BQ=CR=2r

이다.^[1]^{:52, §6}

삼각형 $ABC$ 의 세 변의 길이를 $a=BC$ , $b=AC$ , $c=AB$ 라고 하고, 외심을 $O$ , 내심을 $I$ 라고 하자. 그렇다면 푸르만 삼각형의 세 변의 길이는

F_{B}F_{C}={\sqrt {\frac {(a+b+c)(b+c-a)}{bc}}}OI={\sqrt {\frac {a(a^{3}+b^{3}+c^{3}-(a^{2}b+a^{2}c+ab^{2}+b^{2}c+ac^{2}+bc^{2})+3abc)}{(a-b+c)(a+b-c)}}}

F_{A}F_{C}={\sqrt {\frac {(a+b+c)(a-b+c)}{ac}}}OI={\sqrt {\frac {b(a^{3}+b^{3}+c^{3}-(a^{2}b+a^{2}c+ab^{2}+b^{2}c+ac^{2}+bc^{2})+3abc)}{(b+c-a)(a+b-c)}}}

F_{A}F_{B}={\sqrt {\frac {(a+b+c)(a+b-c)}{ab}}}OI={\sqrt {\frac {c(a^{3}+b^{3}+c^{3}-(a^{2}b+a^{2}c+ab^{2}+b^{2}c+ac^{2}+bc^{2})+3abc)}{(b+c-a)(a-b+c)}}}

이다.^[2]^{:255, §19.15}

삼각형 $ABC$ 의 내심을 $I$ , 외심을 $O$ , 수심을 $H$ , 나겔 점을 $X_{8}$ , 푸르만 원의 중심을 $X_{355}$ 라고 하자. 그렇다면 사각형 $OIX_{355}X_{8}$ 과 사각형 $OIHX_{355}$ 는 모두 평행 사변형이며, 그 무게 중심은 각각 슈피커 중심 및 구점원의 중심이다.^[2]^{:255, §19.15} 특히, 슈피커 중심은 외심과 푸르만원의 중심을 잇는 선분의 중점이며, 구점원의 중심은 내심과 푸르만 원의 중심을 잇는 선분의 중점이다.

삼각형 $ABC$ 의 외접원과 내접원의 반지름을 $R$ 와 $r$ 라고 하자. 그렇다면 내심 $I$ 와 푸르만 원의 중심 $X_{355}$ 사이의 거리는 다음과 같다.^[2]^{:255, §19.15}

IX_{355}=2NI=R-2r

여기서 $N$ 은 구점원의 중심이다.

각주

↑ ^가 ^나 Honsberger, Ross (1995). 《Episodes in Nineteenth and Twentieth Century Euclidean Geometry》. New Mathematical Library (영어) 37. Washington: The Mathematical Association of America. ISBN 0-88385-639-5.
↑ ^가 ^나 ^다 ^라 Douillet, Pierre L. “Translation of the Kimberling's Glossary into Barycentrics” (PDF) (영어). 2020년 5월 31일에 확인함.

외부 링크

Weisstein, Eric Wolfgang. “Fuhrmann circle”. 《Wolfram MathWorld》 (영어). Wolfram Research.
Weisstein, Eric Wolfgang. “Fuhrmann triangle”. 《Wolfram MathWorld》 (영어). Wolfram Research.
Weisstein, Eric Wolfgang. “Fuhrmann center”. 《Wolfram MathWorld》 (영어). Wolfram Research.

[Honsberger-1] 가 ^나 Honsberger, Ross (1995). 《Episodes in Nineteenth and Twentieth Century Euclidean Geometry》. New Mathematical Library (영어) 37. Washington: The Mathematical Association of America. ISBN 0-88385-639-5.

[Douillet-2] 가 ^나 ^다 ^라 Douillet, Pierre L. “Translation of the Kimberling's Glossary into Barycentrics” (PDF) (영어). 2020년 5월 31일에 확인함.

[1]

[2]