strong primes

A prime is said to be strong if it larger than the average of the two surrounding primes

For example, 17 is a strong prime since it is greater than the average of the two surrounding primes 13 and 19.

Primes which are neither balanced nor strong are called weak primes.

The first run of 1,2,..., 12 consecutive strong primes starts at 11, 37, 1657, 1847, 74687, 322193, 5051341, 11938853, 245333213, 397597169, 130272314657, and 1273135176871, respectively.

The first strong primes are 11, 17, 29, 37, 41, 59, 67, 71, 79, 97, 101, 107, 127, 137, 149, 163, 179, 191, 197, 223, 227, 239, 251, 269, 277, 281, 307 more terms

Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

Useful links Wikipedia, Strong prime
OEIS, Sequence A051634

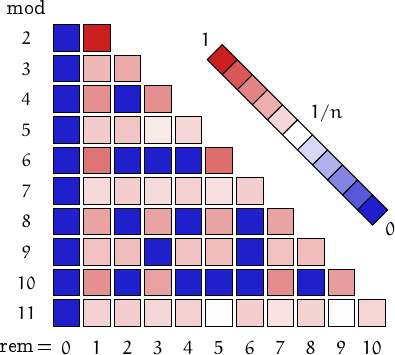
Strong primes can also be... (you may click on names or numbers and on + to get more values)

a-pointer 11 101 631 701 + 99980597 aban 11 17 29 37 + 99000973 alt.fact. 101 4421 alternating 29 41 67 101 + 89898947 amenable 17 29 37 41 + 99999821 apocalyptic 251 499 541 787 + 29983 arithmetic 11 17 29 37 + 9999971 Bell 877 bemirp 1061 1091 1901 10061 + 19091981 c.decagonal 11 101 281 1361 + 99971561 c.heptagonal 71 197 1471 2647 + 99823291 c.pentagonal 331 4951 9151 12781 + 99998251 c.square 41 613 1301 1741 + 99757813 c.triangular 631 4621 7039 7669 + 99988591 Carol 223 16127 Chen 11 17 29 37 + 99999839 congruent 29 37 41 71 + 9999901 constructible 17 65537 Cunningham 17 37 101 127 + 99800101 Curzon 29 41 281 641 + 99996821 cyclic 11 17 29 37 + 9999971 d-powerful 379 739 2063 2137 + 9993623 de Polignac 127 149 251 331 + 99999839 deficient 11 17 29 37 + 9999971 dig.balanced 11 37 41 149 + 67084289 economical 11 17 29 37 + 19999999 emirp 17 37 71 79 + 99999547 equidigital 11 17 29 37 + 19999999 esthetic 67 101 787 12323 + 89876767 Eulerian 11 15619 65519 478271 13824739 evil 17 29 71 101 + 99999547 fibodiv 149 1301 2087 199999 + 21890647 Fibonacci 1597 28657 Friedman 127 347 2503 12107 + 976559 Gilda 29 30571351 good prime 11 17 29 37 + 99927257 happy 79 97 239 331 + 9999929 hex 37 127 331 397 + 99896011 Hogben 307 757 3907 6007 + 99211561 Honaker 457 1049 1091 1301 + 99972703 hungry 17 iban 11 17 41 71 + 777473 idoneal 37 inconsummate 431 461 521 821 + 999953 Jacobsthal 11 43691 2796203 junction 101 107 307 311 + 99999257 katadrome 41 71 97 431 + 98765431 Kynea 79 1087 263167 16785407 Leyland 17 2097593 lonely 16033 1272749 10938023 12623189 Lucas 11 29 521 3571 54018521 lucky 37 67 79 127 + 9999823 m-pointer 2111 13121 15121 19121 + 23311111 magnanimous 11 29 41 67 + 20266681 metadrome 17 29 37 59 + 1456789 modest 29 59 79 311 + 99949999 Motzkin 127 nialpdrome 11 41 71 97 + 99999931 nude 11 oban 11 17 29 37 + 967 odious 11 37 41 59 + 99999959 Ormiston 1931 18397 19031 25013 + 99997897 palindromic 11 101 191 727 + 9980899 palprime 11 101 191 727 + 9980899 pancake 11 29 37 67 + 99510779 panconsummate 11 37 59 127 + 331 pandigital 11 partition 11 101 17977 10619863 pernicious 11 17 37 41 + 9999971 Perrin 17 29 277 367 + 14197 Pierpont 17 37 97 163 + 86093443 plaindrome 11 17 29 37 + 68888999 prime 11 17 29 37 + 99999959 primeval 37 107 137 10139 + 10034579 Proth 17 41 97 641 + 99893249 repdigit 11 repfigit 197 repunit 127 307 757 2801 + 99211561 self 97 277 367 457 + 99998231 self-describing 10153331 10173133 12103331 12163133 + 33322727 sliding 11 29 101 641 Sophie Germain 11 29 41 179 + 99999611 star 37 541 937 2053 + 99364981 strobogrammatic 11 101 18181 19861 + 69911669 super-d 107 127 269 281 + 9999419 tetranacci 29 tribonacci 149 trimorphic 251 499 751 1249 + 4999999 truncatable prime 17 29 37 59 + 99951283 twin 11 17 29 41 + 99999587 uban 11 17 29 37 + 99000023 Ulam 11 97 197 431 + 9999877 undulating 101 191 727 757 + 1616161 upside-down 37 1289 3467 3557 + 99919111 weakly prime 505447 584141 604171 1062599 + 99595919 Wieferich 3511 Woodall 17 191 590489 14680063 Zuckerman 11 zygodrome 11 11777 22277 22777 + 99955577