A prime number 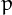 is a Chen prime
if
is a Chen prime
if 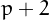 is either a prime or a semiprime.
is either a prime or a semiprime.
Jing Run Chen, after which they are named, proved in 1966 that there are infinite such primes.
Binbin Zhou has proved in 2009 that the Chen primes contain arbitrarily long arithmetic progressions.
The smallest 3 × 3 magic square whose entries are Chen primes is
| 47 | 113 | 17 |
| 29 | 59 | 89 |
| 101 | 5 | 71 |
The first Chen primes are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 47, 53, 59, 67, 71, 83, 89, 101, 107, 109, 113, 127, 131, 137, 139, 149, 157, 167, 179, 181, 191, 197, 199, 211, 227, 233, 239, 251, 257 more terms
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
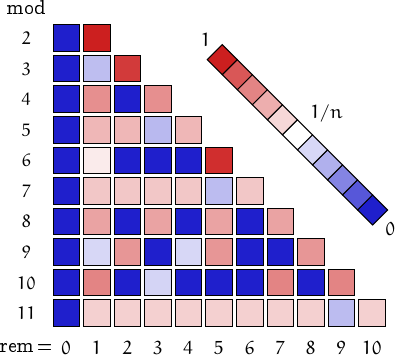
Chen primes can also be... (you may click on names or numbers and on + to get more values)
a-pointer
11
13
101
181
+
99986539
aban
11
13
17
19
+
99000953
alt.fact.
19
101
4421
alternating
23
29
41
47
+
89898929
amenable
13
17
29
37
+
99999721
apocalyptic
157
251
443
499
+
29927
arithmetic
11
13
17
19
+
9999991
balanced p.
53
157
211
257
+
99999617
Bell
877
bemirp
1061
1091
1601
1901
+
19880981
c.decagonal
11
31
101
211
+
99971561
c.heptagonal
71
197
953
1471
+
99785911
c.pentagonal
31
181
1381
11731
+
99335281
c.square
13
41
113
181
+
99531941
c.triangular
19
31
109
199
+
99988591
Carol
47
16127
congruent
13
23
29
31
+
9999991
constructible
17
257
65537
Cunningham
17
31
37
101
+
99720197
Curzon
29
41
53
89
+
99996821
cyclic
11
13
17
19
+
9999991
d-powerful
89
379
2179
2243
+
9979337
de Polignac
127
149
251
337
+
99999839
deficient
11
13
17
19
+
9999991
dig.balanced
11
19
37
41
+
67084289
economical
11
13
17
19
+
19999739
emirp
13
17
31
37
+
99999827
equidigital
11
13
17
19
+
19999739
esthetic
23
67
89
101
+
67678789
Eulerian
11
65519
478271
evil
17
23
29
53
+
99999971
fibodiv
19
47
149
199
+
67645819
Fibonacci
13
89
233
514229
Friedman
127
347
12107
15641
+
995341
Gilda
29
683
2207
good prime
11
17
29
37
+
99927257
happy
13
19
23
31
+
9999991
hex
19
37
127
631
+
97179517
Hogben
13
31
157
211
+
99790111
Honaker
131
263
1039
1049
+
99973061
hungry
17
2003
iban
11
17
23
41
+
777317
iccanobiF
13
4139
idoneal
13
37
inconsummate
431
443
461
491
+
999149
Jacobsthal
11
683
2731
43691
junction
101
107
109
113
+
99999257
katadrome
31
41
53
71
+
9875321
Kynea
23
66047
Leyland
17
32993
lonely
23
53
211
2179
+
1272749
Lucas
11
29
47
199
+
3010349
lucky
13
31
37
67
+
9999397
m-pointer
23
2111
11261
11621
+
14111131
magnanimous
11
23
29
41
+
48804809
metadrome
13
17
19
23
+
23456789
modest
13
19
23
29
+
99959999
Motzkin
127
15511
nialpdrome
11
31
41
53
+
99999971
nude
11
oban
11
13
17
19
+
983
odious
11
13
19
31
+
99999839
Ormiston
1913
1931
18397
19013
+
99999131
palindromic
11
101
131
181
+
9981899
palprime
11
101
131
181
+
9981899
pancake
11
29
37
67
+
99510779
panconsummate
11
23
31
37
+
1291
pandigital
11
19
partition
11
101
pernicious
11
13
17
19
+
9999991
Perrin
17
29
14197
43721
Pierpont
13
17
19
37
+
57395629
plaindrome
11
13
17
19
+
88888999
prime
11
13
17
19
+
99999971
primeval
13
37
107
113
+
10034579
Proth
13
17
41
113
+
99893249
repdigit
11
repfigit
19
47
197
1084051
repunit
13
31
127
157
+
99790111
self
31
53
211
233
+
99999827
self-describing
10153331
10322321
12103331
12193133
+
33322727
sliding
11
29
101
641
Sophie Germain
11
23
29
41
+
99999611
star
13
37
181
337
+
98050837
straight-line
4567
23456789
strobogrammatic
11
101
181
116911
+
69911669
strong prime
11
17
29
37
+
99999839
super-d
19
31
107
127
+
9999931
tetranacci
29
401
tribonacci
13
149
trimorphic
251
499
751
4999
281249
truncatable prime
13
17
23
29
+
99979337
twin
11
13
17
19
+
99999587
uban
11
13
17
19
+
98000059
Ulam
11
13
47
53
+
9999161
undulating
101
131
181
191
+
1616161
upside-down
19
37
1289
1559
+
99791311
weak prime
13
19
23
31
+
99999971
weakly prime
584141
971767
1062599
4393139
+
99778351
Wieferich
3511
Woodall
17
23
191
524287
590489
Zuckerman
11
zygodrome
11
11177
11777
22277
+
99955577