A prime 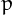 is a Pierpont prime if it can be
written as
is a Pierpont prime if it can be
written as 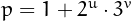 , for
, for 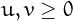 .
.
A.M.Gleason has proved that a regular
polygon of sides can be constructed by ruler, compass and
angle-trisector if and only if
, where the
's
are distinct Pierpont primes.
Compare with the polygons constructible with ruler and compass only.
The first Pierpont primes are 2, 3, 5, 7, 13, 17, 19, 37, 73, 97, 109, 163, 193, 257, 433, 487, 577, 769, 1153, 1297, 1459, 2593, 2917, 3457, 3889, 10369, 12289, 17497, 18433, 39367, 52489, 65537, 139969, 147457, 209953 more terms
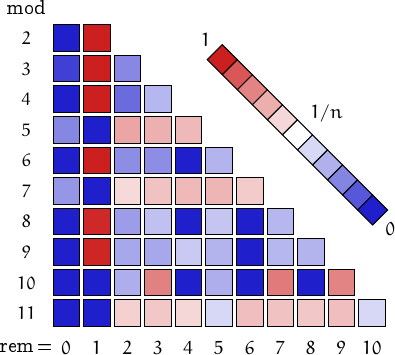
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
Pierpont primes can also be... (you may click on names or numbers and on + to get more values)
a-pointer
13
1153
aban
13
17
19
37
73
97
109
163
193
257
433
487
577
769
alt.fact.
19
alternating
109
163
769
10369
amenable
13
17
37
73
97
109
193
257
433
577
+
120932353
169869313
483729409
725594113
apocalyptic
2593
3889
10369
12289
17497
18433
arithmetic
13
17
19
37
73
97
109
163
193
257
+
2654209
5038849
5308417
8503057
balanced p.
257
18433
c.square
13
c.triangular
19
109
Chen
13
17
19
37
109
257
487
577
769
1297
+
629857
995329
5308417
57395629
congruent
13
37
109
257
487
2917
39367
331777
839809
5308417
constructible
17
257
65537
Cunningham
17
37
257
577
1297
2917
65537
147457
331777
746497
+
6347497291777
14281868906497
39582418599937
142657607172097
cyclic
13
17
19
37
73
97
109
163
193
257
+
2654209
5038849
5308417
8503057
d-powerful
3457
de Polignac
629857
746497
1492993
86093443
deficient
13
17
19
37
73
97
109
163
193
257
+
2654209
5038849
5308417
8503057
dig.balanced
19
37
163
economical
13
17
19
37
73
97
109
163
193
257
+
8503057
11337409
14155777
19131877
emirp
13
17
37
73
97
769
1153
3889
12289
995329
1179649
120932353
equidigital
13
17
19
37
73
97
109
163
193
257
+
8503057
11337409
14155777
19131877
evil
17
163
257
1297
2593
10369
17497
65537
139969
331777
+
120932353
169869313
483729409
725594113
fibodiv
19
Fibonacci
13
Friedman
139969
147457
209953
472393
629857
786433
good prime
17
37
97
257
3457
65537
happy
13
19
97
109
193
487
52489
hex
19
37
Hogben
13
73
hungry
17
iban
17
73
iccanobiF
13
idoneal
13
37
inconsummate
65537
junction
109
2917
786433
katadrome
73
97
Leyland
17
lucky
13
37
73
163
193
433
487
577
769
1459
+
39367
147457
209953
5038849
metadrome
13
17
19
37
257
1459
3457
modest
13
19
109
433
nialpdrome
73
97
433
oban
13
17
19
37
73
97
577
769
odious
13
19
37
73
97
109
193
433
487
577
+
28311553
63700993
113246209
258280327
pancake
37
panconsummate
37
73
257
pandigital
19
pernicious
13
17
19
37
73
97
109
193
257
433
+
1492993
1769473
1990657
8503057
Perrin
17
plaindrome
13
17
19
37
257
577
1459
3457
3889
12289
prime
13
17
19
37
73
97
109
163
193
257
+
206158430209
251048476873
347892350977
880602513409
primeval
13
37
Proth
13
17
97
193
257
577
769
1153
3457
10369
+
123834728449
206158430209
347892350977
880602513409
repfigit
19
repunit
13
73
self
97
2593
18433
star
13
37
73
433
strong prime
17
37
97
163
487
769
1297
3457
39367
52489
+
8503057
28311553
71663617
86093443
super-d
19
769
10369
17497
139969
331777
tribonacci
13
truncatable prime
13
17
37
73
97
twin
13
17
19
73
109
193
433
1153
2593
65537
+
995329
57395629
63700993
169869313
uban
13
17
19
37
73
97
Ulam
13
97
10369
629857
1990657
upside-down
19
37
73
weak prime
13
19
73
109
193
433
577
1153
1459
2593
+
14155777
19131877
57395629
63700993
Woodall
17