A number 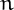 is pandigital in base
is pandigital in base  if its base
if its base  representation contains all the possible digits, i.e., 0, 1, ..., b-1, at least once.
representation contains all the possible digits, i.e., 0, 1, ..., b-1, at least once.
If contain each digit exactly once, it is called strictly pandigital.
For example, 1023456789 is the smallest (strictly) pandigital number in base 10, while is pandigital in base 4 but not strictly pandigital.
Many authors use simply the term pandigital to mean both kind of numbers, so I will do the same, since usually the right meaning will be clear from the contest.
The first strictly pandigital numbers, in any possible base are
2, 11, 15, 19, 21, 75, 78, 99, 108, 114, 120, 135, 141, 147, 156, 177, 180, 198, 201, 210, 216, 225, 228, 694, 698, 714, 722, 738, 742, 894 more terms
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

A graph displaying how many pandigitals are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Pandigitals can also be... (you may click on names or numbers and on + to get more values)
a-pointer
11
ABA
722
1922
6002500
+
9743521608
aban
11
15
19
+
380000948
abundant
78
108
114
+
47754948
Achilles
108
128547
254043
+
9876523104
admirable
78
114
120
+
95510716
alt.fact.
19
alternating
21
78
141
+
298989892
amenable
21
108
120
+
381367044
amicable
1210
124155
525915
+
5209468173
apocalyptic
714
894
898
+
29965
arithmetic
11
15
19
+
9998170
astonishing
15
216
Bell
15
betrothed
75
2573840619
binomial
15
21
78
+
9654871320
brilliant
15
21
c.decagonal
11
c.heptagonal
94986116
104550916
108762676
+
229946956
c.nonagonal
2926
23005
29890
+
339861556
c.octagonal
225
38025
314721
+
9614783025
c.pentagonal
141
69129556
91279516
+
380103076
c.square
21425
27145
42925
c.triangular
19
694
1054
+
377047756
cake
15
383439
Chen
11
19
congruent
15
21
78
+
9998037
constructible
15
120
20560
30720
cube
216
Cunningham
15
99
120
+
9743861520
Curzon
21
78
114
+
16434369
cyclic
11
15
19
+
9997981
D-number
15
21
141
+
799899
d-powerful
135
1634
2134
+
9977513
de Polignac
16405
17735
23935
+
16433683
decagonal
742
22275
124785
+
9576432810
deficient
11
15
19
+
9998163
dig.balanced
11
15
19
+
199999932
double fact.
15
Duffinian
21
75
201
+
9998163
eban
2054
30040
30050
+
66060044
economical
11
15
19
+
16434817
emirpimes
15
177
1202
+
16421923
equidigital
11
15
19
+
16434817
eRAP
709929
89271996
185164700
+
8460391257
esthetic
21
78
210
+
9876543210
Eulerian
11
120
evil
15
75
78
+
381367044
factorial
120
fibodiv
19
75
32525
+
1042765893
Fibonacci
21
Friedman
216
1022
10575
+
781263
frugal
11045
12125
21870
+
379233148
gapful
108
120
135
+
9876543210
Gilda
78
990
good prime
11
happy
19
694
970
+
9998037
harmonic
2178540
Harshad
21
108
114
+
9876543210
heptagonal
970
785961
2207590
+
9386472150
hex
19
2252467
3124261
+
13337317
hexagonal
15
120
8385
+
9654871320
highly composite
120
180
hoax
2826
2902
8415
+
95581084
Hogben
21
217623
228963
+
15401701
house
78
13600909
hyperperfect
21
iban
11
21
114
+
774411
idoneal
15
21
78
+
210
inconsummate
75
216
1646
+
800661
interprime
15
21
99
+
95583996
Jacobsthal
11
21
699051
Jordan-Polya
120
216
30720
junction
210
216
1014
+
95584540
Kaprekar
99
5479453
katadrome
21
75
210
+
9876543210
Lehmer
15
16405
39865
+
14821261
Leyland
177
lonely
120
Lucas
11
lucky
15
21
75
+
9998163
Lynch-Bell
15
135
216
3817296
magic
15
210975
magnanimous
11
21
970
+
42265
metadrome
15
19
78
+
124689
modest
19
1022
2022
+
1980467532
Moran
21
114
156
+
95454108
Motzkin
21
41835
narcissistic
1634
nialpdrome
11
21
75
+
9876543210
nonagonal
75
170391
598851
+
9762483051
nude
11
15
99
+
379772316
O'Halloran
156
oban
11
15
19
+
990
octagonal
21
225
12545
+
9053782416
odious
11
19
21
+
381366972
palindromic
11
99
141
+
298989892
palprime
11
pancake
11
742
1654
+
341270876
panconsummate
11
15
21
78
partition
11
15
135
239943
pentagonal
210
2882
16485
+
9120345876
pernicious
11
19
21
+
800661
persistent
1023456789
1023456879
1023457689
+
9876543210
Pierpont
19
plaindrome
11
15
19
+
334466788
Poulet
39865
212421
5258701
+
8137633
power
216
225
38025
+
9814072356
powerful
108
216
225
+
9876523104
practical
78
108
120
+
9998058
prim.abundant
78
114
894
+
95510716
prime
11
19
primorial
210
pronic
156
210
1190
+
9854632170
Proth
177
225
11265
+
8736210945
pseudoperfect
78
108
114
+
797895
repdigit
11
99
repfigit
19
75
742
repunit
15
21
156
+
15401701
Rhonda
13521354
Ruth-Aaron
15
78
714
+
9723805461
Saint-Exupery
20580
30720
33600
+
8439576120
self
75
108
198
+
381366956
semiprime
15
21
141
+
16434817
sliding
11
16265
200432500
Smith
2902
9015
19615
+
95580940
Sophie Germain
11
sphenic
78
114
742
+
16434201
square
225
38025
314721
+
9814072356
straight-line
135
147
210
+
9876543210
strobogrammatic
11
88669988
91196116
strong prime
11
super Niven
120
210
990
+
360033300
super-d
19
1054
1070
+
9998058
superabundant
120
180
tau
108
156
180
+
381367044
taxicab
11548089
1430867592
3928157064
+
9083647125
tetrahedral
120
37820
43680
+
131908700
tetranacci
15
108
1490
triangular
15
21
78
+
9654871320
trimorphic
75
99
twin
11
19
uban
11
15
19
+
69000020
Ulam
11
99
114
+
9998037
undulating
141
898
8585
+
434343
unprimeable
894
898
1070
+
9998058
untouchable
120
210
216
+
44760
upside-down
19
2558
124689
+
282951828
vampire
15249780
80993700
81739588
+
8210953476
wasteful
75
78
99
+
9998170
weak prime
19
weird
10570
13790
26110
30170
Wieferich
298389
Zeisel
25085
Zuckerman
11
15
135
+
13226976
Zumkeller
78
108
114
+
44790
zygodrome
11
99
33555
+
339955500