cake numbers

Cake number $C_n$

represents the maximal number of pieces in which a cake (or a cube) can be divided into by $n$

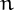planar cuts. They are the tridimensional version of pancake numbers.

In general,

$C_n = {n+1\choose3}+n+1 = {n\choose3}+ {n\choose2}+ {n\choose1}+ {n\choose0}=\frac{n^3+5n+6}{6}\,.$

Note that with the first 3 cuts it is possible to divide the cake into 2, then 4 and finally 8 pieces, but it is impossible to cut each of the 8 pieces with a fourth cut, and indeed $C_4$ is only 15, not 16.

The first cake numbers are 1, 2, 4, 8, 15, 26, 42, 64, 93, 130, 176, 232, 299, 378, 470, 576, 697, 834, 988, 1160, 1351, 1562, 1794, 2048, 2325, 2626, 2952, 3304, 3683, 4090, 4526, 4992, 5489, 6018, 6580, 7176, 7807 more terms

Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

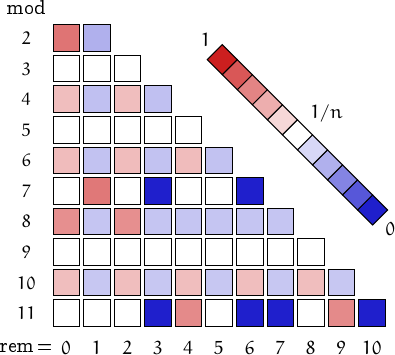
A graph displaying how many cake numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Useful links Mathworld, Cube Division by Planes
Wikipedia, Cake number
OEIS, Sequence A000125

Cake numbers can also be... (you may click on names or numbers and on + to get more values)

ABA 64 2048 aban 15 26 42 64 + 823031000090 abundant 42 176 378 576 + 49235272 admirable 42 834 alternating 232 470 834 2325 + 494561274 amenable 64 93 176 232 + 998152597 apocalyptic 1160 1351 1562 2325 + 29317 arithmetic 15 42 93 299 + 9886826 astonishing 15 Bell 15 binomial 15 378 brilliant 15 299 697 c.triangular 64 1004914 Catalan 42 congruent 15 93 299 470 + 9963072 constructible 15 64 2048 82240 cube 64 Cunningham 15 26 310248 804610 3940224 Curzon 26 378 470 834 + 195151790 cyclic 15 299 697 1351 + 9735503 D-number 15 93 d-powerful 378 2048 2626 82240 + 7207552 de Polignac 7807 29317 166751 288101 + 91895351 decagonal 232 2626 deceptive 859964833 deficient 15 26 64 93 + 9886826 dig.balanced 15 42 232 3304 + 199065882 double fact. 15 Duffinian 64 93 299 576 + 9735503 eban 42 64 economical 15 64 1351 2048 + 19250624 emirpimes 15 26 93 7807 + 87919693 enlightened 2048 equidigital 15 64 1351 11522 + 19250624 esthetic 232 Eulerian 26 evil 15 130 232 378 + 999802434 Friedman 2048 12384 121576 234249 + 383439 frugal 2048 40495625 75203584 129359360 + 488392192 gapful 130 176 1160 2325 + 99739632104 happy 130 176 4090 12384 + 8580119 Harshad 42 378 576 1160 + 9886503251 heptagonal 697 hexagonal 15 378 hoax 2325 32568 50184 91964 + 82173826 hyperperfect 697 iban 42 470 3304 10701 + 447720 idoneal 15 42 93 130 232 impolite 64 2048 inconsummate 834 4526 5489 10701 + 893376 interprime 15 26 42 64 + 94954490 Jordan-Polya 64 576 2048 junction 6018 9920 30914 41728 + 91895351 Kaprekar 17344 katadrome 42 64 93 Lehmer 15 1351 3658901 29269801 lucky 15 93 23479 29317 + 9437505 Lynch-Bell 15 12384 magic 15 magnanimous 130 metadrome 15 26 378 23479 modest 26 299 4090 6018 + 1965015327 Moran 42 nialpdrome 42 64 93 988 + 988442 nonagonal 1794 nude 15 12384 1848448 13344192 + 264888384 oban 15 26 93 378 + 988 octagonal 176 1160 odious 26 42 64 93 + 998152597 palindromic 232 10701 pancake 232 15226 panconsummate 15 pandigital 15 383439 partition 15 42 176 pentagonal 176 47972 17862376 pernicious 26 42 93 130 + 9886826 persistent 37054129568 97694358210 plaindrome 15 26 299 378 23479 power 64 576 2048 67600 75203584 powerful 64 576 2048 67600 75203584 practical 42 64 176 378 + 9963072 prim.abundant 42 834 721928 1949704 5564644 pronic 42 2635752 pseudoperfect 42 176 378 576 + 956040 repunit 15 Ruth-Aaron 15 37882 956040 39721851 self 42 64 176 299 + 993213978 semiprime 15 26 93 299 + 89231899 Smith 378 576 215930 234249 + 97031176 sphenic 42 130 470 834 + 98080778 square 64 576 67600 75203584 super-d 988 10701 19650 22152 + 9002008 tau 232 2952 4992 12384 + 944720768 tetranacci 15 triangular 15 378 uban 15 26 42 93 Ulam 26 5489 27776 34280 + 9886826 undulating 232 2626 unprimeable 1794 2048 2325 8474 + 9585732 untouchable 576 1160 2048 2952 + 956040 upside-down 64 wasteful 26 42 93 130 + 9963072 Zuckerman 15 Zumkeller 42 176 378 834 + 95368