Хипарх

Хипарх (грчки Ἵππαρχος; око 190. пне. – око 120. пне.), грчки астроном, географ и математичар. ЕСА је једно своје истраживање, Хиппарцос Спаце Астрометрy Миссион, назвала управо по њему.

Хипарх се родио у Ницеји (данас Изник у Турској), а умро вјеројатно на отоку Роду. Познато је да је дјеловао најраније од 147. пне. до 127. пне. Сматра се највећим астрономским проматрачем, а по некима и највећим античким астрономом. Био је први Грк који је развио квантитативне и поуздане моделе сунчева и мјесечева гибања користивши проматрања и знања која су стољећима скупљали Калдејци из Бабилоније. Први је саставио тригонометријске таблице које су му омогућавале рјешавање сваког трокута. Са својим теоријама о гибању Сунца и Мјесеца, те својом бројчаном тригонометријом био је вјеројатно први који је развио поуздану методу предвиђања помрчина Сунца. Остала његова постигнућа укључују откриће прецесије, састављање првог звјезданог каталога и вјеројатно откриће астролаба. Клаудије Птоломеј се три стољећа касније много ослањао на Хипарха. Хипархова је синтеза астрономије надмашила његов рад. Иако је написао најмање 14 књига, једино су се његови коментари на Аратов популарни астрономски еп сачували од каснијих преписивача. Због тога се јако мало зна о Хипарху.

Извори из којих добивамо већину знања о Хипарховом животу и дјелу су Птоломејев (2. стољеће пне.) Алмагест ("Велика расправа"), Страбонова Геограпхиа ("Географија"), Плинијева Натуралис хисториа ("Повијест природе"; 1. стољеће^[1]., те додатни извјештаји које су написали Паппус и Теон из Александрије (4. стољеће пне.) у својим коментарима на Алмагест.

Према традицији Хипарх је рођен у Ницеји (грчки Νικαία), антички округ Битинија, (данашњи İзник у провинцији Бурса у Турској).

Точни датуми Хипархова живота нису познати, али му Птоломеј приписује астрономска проматрања од 147. пне. до 127. пне. Хипарх је можда направио проматрања и прије 162. пне. Датум његова рођења (око 190. пне.) је израчунао Деламбре на темељу трагова у његовом раду. Хипарх је вјеројатно живио и неколико година послије 127. пне. јер је испитао и објавио своја задња проматрања. Он је користио информације из Александрије једнако као из Бабилона, међутим не зна се да ли је икада и посјетио та мјеста.

Није познато каква су била Хипархова новчана средства нити како је припомагао своје знанствено дјеловање. Такођер није познат ни његов изглед јер нису пронађени његови портрети из тог времена. Међутим, његово се име исписивало на новцу кованом у 2. и 3. стољећу у Битинији у његову част на којима је приказан заједно с глобус. То потврђује традицију по којој се ондје родио.

Вјерује се да је Хипарх умро на отоку Роду гдје је провео већи дио својега каснијег живота. Птоломеј му приписује проматрања с Рода у раздобљу између 141. пне. и 127. пне.

Хипархова главна изворна дјела су изгубљена. Његово једино сачувано дјело је Тоон Аратоу каи Еудоxоу Фаиноменоон еxегесис ("Коментар о Еудоксовим и Аратовим Појавама"). То је критички коментар у двије књиге на популарни Аратов еп темељен на Еудоксову дјелу^[2] Објавио га је Карл Манитиус (Ин Арати ет Еудоxи Пхаеномена, Леипзиг, 1894.). Хипарх је такођер направио попис својих главних дјела у којем је јасно навео око 14 књига које су познате једино по спомињају каснијих аутора. Његов славни звјездани каталог је вјеројатно убачен у Птоломејев, па се не може поуздано реконструирати. Зна се да је Хипарх направио небески глобус. Копија копије тог глобуса можда је сачувана у најстаријем сачуваном небеском глобусу који поуздано приказује звијежђа. Глобус је држао Фарнесеов Атлас.

Хипарх је познат као утемељитељ и отац знанствене астрономије. Вјерује се да је био највећи грчки астрономски проматрач, а многи га сматрају и највећим астрономом античких времена, Цицерон је дао ту предност Аристарху из Самоса, док неки ту част дају Птоломеју из Александрије. Хипархове рукописе су замјенили Птоломејеви, па их каснији преписивачи нису сачували за будуће нараштаје.

Многа дјела грчких знанственика – математичара, астронома и географа –сачувана су до данашњих дана, а кроз каснија навођења познати су и неки дијелови њихових мисли и дјела. Међутим, постигнућа цивилизација Средњег истока, посебно Бабилонаца, била су заборављена у тим подручјима. Након открића археолошких налазишта у 19. стољећу, пронађени су многи рукописи на глиненим плочицама од којих су се неки односили на астрономију.

Након поновног открића бабилонске цивилизације постало је јасно да су грчки астрономи, посебице Хипарх, користили многа знања од Калдејаца^[3].

Птоломеј је тврдио у својем Алмагесту IV.2 да је Хипарх поправио вриједности мјесечевог периода која су му била позната од "још старијих астронома" успоређујући своја проматрања помрчина и она која су још прије извршили Калдејци. Периоди које Птоломеј приписује Хипарху били су кориштени у бабилонским ефемеридама, те посебно у збирци текстова која се данас назива "Сустав Б" (понекад приписан Кидиннуу)^[4] . Очигледно Хипарх је само потврдио ваљаност периода, које је научио од Калдејаца, у својим новим проматрањима.

Јасно је да је Хипарх (а након њега и Птоломеј) имао цјеловит попис проматрања помрчина кроз многа стољећа. Највјеројатније су та проматрања састављена с "дневних" плочица. То су глинене плочице на којима су записана сва значајна проматрања која су Калдејци свакодневно обављали. Сачувани примјерци датирају од 652. пне. до 130. по. Кр., иако је вјеројатно да потјечу од владавине бабилонског краља Набонасара па надаље. Своју кронологију Птоломеј започиње управо с првим даном египатског календара прве године Набонасарове владавине, тј. 26. вељаче 747. пне.

Глина је као сировина сама по себи тешка за употребу, па су без сумње Калдејци саставили изватке од нпр. свих проматраних помрчина (пронађене су плочице с пописом свих помрчина у временском раздобљу које покрива сарос). То им је омогућило да препознају периодична појављивања догађаја. Међу осталима користили су у Суставу Б (усп. Алмагест IV.2):

• 223 (синодичка) мјесеца = 239 повратка у неправилности или аномалији (аномалистички мјесец) = 242 повратка у ширини (драконски мјесец). То је данас познато као сарос раздобље које је корисно у предвиђању помрчина.
• 251 (синодички) мјесец = 269 повратка у аномалији
• 5458 (синодички) мјесец = 5923 повратка у ширини
• 1 синодички мјесец = 29;31:50:08:20 дана (сексагезимални сустав; 29.53059413... дана у декадском суставу = 29 дана 12 сати 44 мин 3⅓ с)

Бабилонци су изражавали сва раздобља у синодичким мјесецима јер су вјеројатно користили лунисоларни календар. Различити односи у годишњим појавама довели су до различитих вриједности за дужину године.

На једнак начин били су познати различити односи између периода планета. Односи које је Птоломеј приписао Хипарху у Алмагесту IX.3 већ су се користили у предвиђањима која су пронађенима на бабилонским глиненим плочицама.

Сва та знања пренесена су Грцима убрзо након освајања Александра Великога (331. пне.). Према каснокласичном филозофу Симплицију (рано 6. стољеће пне.), Александар је наредио превођење повијесних астрономских записа под надзором његова кроничара Калистена из Олинта који их је послао својем ујаку Аристотелу. Треба споменути да иако је Симплиције јако касни извор, његови прорачуни могу бити поуздани. Он је провео неко вријеме у прогонству на Сасанидском (перзијском) двору, те је ондје могао приступити изворима који су иначе били изгубљени на Западу. Запањујуће је што он спомиње наслов тèресис (грч. стражар) што је необични назив за повијесно дјело, а заправо је примјерен пријевод бабилонског наслова массарту што значи "чувати" али и "проматрати". У то вријеме Аристотелов ученик Калип из Кизика уводи 76-годишњи циклус који је побољшан 19-годишњим Метоновим циклусом. Прва година његовог првог циклуса започела је на љетни сунцостај 28. липња 330. пне. (јулијански пролептички датум), али чини се да је касније убројио лунарне мјесеце из првог мјесеца након Александрове одлучне битке код Гаугамеле у јесен 331. пне. Калип је могао узети своје податке из бабилонских извора, а његов је календар могао Кидинну наслутити. Такођер зна се да је бабилонски свећеник Берос написао око 281. пне. за новог владара Антиоха I књигу на грчком о (претежито митолошкој) бабилонској повијести, Бабилониака. Он је касније основао школу астрологије на грчком отоку Косу. Такођер је Грке могао поучити астрономију, тј. астрологију и Судин који се налазио на двору Атала Сотера у касном 3. стољећу пне.

Пријевод астрономских записа је у сваком случају тражио темељито знање о писму, језику, и начину поступања, па се чини као да су то учинили неки непознати Калдејци. Бабилонци су сада уписивали своја проматрања у властитом календару у којем су мјесеци и године имали различиту дужину (по 29 или 30 дана; односно 12 или 13 мјесеци). Отада они више нису користили уобичајени календар (који се темељио на Метоновом циклусу), него су започели нови мјесец темељен на проматрањима младог Мјесеца. То је учинило израчунавање времена између појединих догађаја врло дуготрајним.

Хипарх је претворио те записе у египатски календар који је имао увијек утврђену годину од 365 дана (који се састоје од 12 мјесеци, 30 дана и 5 додатних дана). То је учинило израчунавање времена много лакшим. Птоломеј је сва своја проматрања одређивао по том календару. Птоломеј је такођер написао да "све што је он (=Хипарх) учинио било је састављање планетарних проматрања који су били уређени на много кориснији начин" (Алмагест IX.2). Плиније тврди (Натуралис Хисториа II.IX(53)) у предвиђањима помрчина: "Након њиховог времена (=Талес) Хипарх је предвидио смјер кретања обију звијезда (=Сунца и Мјесеца) за 600 година, ...". Чини се да то значи да је Хипарх предвидио помрчине у раздобљу од 600 година, али узимајући у обзир огромне количине потребног рачунања, то се чини врло невјеројатним. Хипарх би заправо направио попис свих помрчина од Набонасарова до својега времена.

Остали трагови бабилонског искуства у Хипарховом раду јесу:

• први Грк познат по диоби круга у 360 ступњева по 60 лучних минута.
• прва досљедна употреба сексагезималног бројчаног сустава.
• употреба јединице пецхус ("лакат") од око 2° или 2½°.
• употреба кратког раздобља од 248 дана = 9 аномалистичких мјесеци.

Хипарх је познат као први математичар који је саставио тригонометријске таблице. Оне су му требале приликом рачунања ексцентричности орбите Сунца и Мјесеца. Уврстио је у таблицу вриједности за тетивне функције које показују дужину тетиве за сваки кут. То је направио користивши круг с опсегом од 21600 и полумјером од (заокружено) 3438 јединица. Те јединице су биле дуге 1 лучну минуту дуж опсега. Направио је таблицу с вриједностима функција за кутове с разлико од 7.5°. У модерној терминологији, тетива кута једнака је двоструком синусу половице тог кута, тј.:

тетива(А) = 2 син(А/2).

Теон из Александрије (4. стољеће) је у својему осврту на Алмагест I.10 споменуо дјело (данас изгубљено) тоон ен куклоои еутхеиоон (О дуљинама унутар круга) у којем је Хипарх описао своје постигнуће. Чини се да је његова таблица сачувана у астрономским рукописима у Индији, примјерице Сурyа Сидханта. То је било значајно откриће јер је допустило грчким астрономима да ријеше сваки трокут, а учинило је могућим стварање квантитативних астрономских модела и предвиђања користивши одређене геометријске технике^[5].

За своје тригонометријске таблице Хипарх је морао користити бољу апроксимацију за π од оне коју је користио Архимед (између 3 + 1/7 и 3 + 10/71): Можда је користио Птоломејеву апроксимацију: 3;8:30 (сексагезимално) (Алмагест VI.7);. Међутим није познато ни је ли сâм израчунао побољшану вриједност.

Хипарх је могао направити тригонометријске таблице користећи Питагорин и Архимедов поучак. Можда је развио и користио поучак у планарној геометрији касније названог Птоломејев поучак, јер га је доказао Птоломеј у свом Алмагесту (I.10) (касније га је разрадио Царнот).

Хипарх је био први који је показао да је стереографска пројекција конформална и да трансформира кругове на сфери који не пролазе средиштем пројекције на кругове на равнини. То је био темељ конструкцији астролаба.

Уз геометрију, Хипарх је такођер користио калдејске аритметичке технике. Био је и један од првих грчких математичара који је на тај начин проширио технике доступне астрономима и географима.

Ипак не постоје назнаке да је Хипарх познавао сферну тригонометрију коју је први развио тек Менелај из Александрије у 1. стољећу. Птоломеј је касније користио нову технику израчунавања примјерице почетне и завршне точке помрчине или мјесечеве паралаксе. Хипарх је можда за то користио глобус (како би очитао вриједности на координатним правцима нацртаним на њему) као и апроксимације из планарне геометрије или аритметике које су развили Калдејци.

Хипарх је такођер проучавао гибање Мјесеца, те је потврдио поуздане вриједности неких периода мјесечева гибања које су калдејски астрономи знали прије њега. Традиционална средња вриједност (из бабилонског Сустава Б) синодичког мјесеца је 29 дана;31,50,8,20 (сексагезимално) = 29.5305941... д . Изражено као 29 дана + 12 сати + 793/1080 сати ова вриједност је кориштена касније у хебрејском календару (вјеројатно из бабилонских извора). Калдејци су такођер знали да 251 синодичких мјесеци = 269 аномалистичких мјесеци. Хипарх је проширио тај период за фактор од 17, јер би након тога интервала Мјесец такођер имао сличну дужину и близу је цијелом броју година (345). Стога би се помрчине наново јављале под скоро идентичним околностима. Период је дуг 126007 дана 1 сат (заокружено). Хипарх је могао потврдити своја израчунавања успоређујући помрчине из својега времена (вјеројатно 27. сијечња 141. пне. и 26. просинца 139. пне.) и оних из бабилонских извора 345 година раније (Алмагест IV.2). Већ су ал-Бируни (Qанун VII.2.II) и Коперник (Де револутионибус IV.4) записали да је период од 4267 синодичких мјесеци заправо око 5 минута дужи од вриједности за период помрчине коју Птоломеј приписује Хипарху. Ипак, најбољи сатови и методе мјерења времена тог доба имали су поузданост не више од 8 минута. Модерни знанственици се слажу да је Хипарх заокружио период помрчине на најближи сат и користио је то да потврди ваљаност традиционалних вриједности више него да покуша извести побољшану вриједност из властитих проматрања. Уз модерне ефемериде и узимања рачуна за промјену дуљине дана (види ΔТ) процјењује се да је грешка у привидној дужини синодичког мјесеца била мања од 0.2 с у 4. стољећу пр. Кр. и мања од 0.1 с у Хипархово вријеме.

Дуго времена је било познато да гибање Мјесеца није једнолико, већ његова брзина варира. То се зове његовом аномалијом и понавља се с властитим периодом; аномалистичким мјесецом. Калдејци су то израчунали аритметички, те су користили таблице у којима су давали дневно гибање Мјесеца према датуму тијеком дужег раздобља. Грци су пак више вољели размишљати о геометријским небеским тијелима. Аполоније из Перга је на крају 3. стољећа пне. предложио два модела за мјесечево и планетарно гибање:

1. У првоме моделу Мјесец би се кретао једнолико дуж кружнице, али Земља би била ексцентрична, тј. у одређеној удаљености од средишта кружнице. Тако би видљива кутна брзина Мјесеца (и његова удаљеност) варирала.
2. Сам Мјесец би се кретао једнолико (са средњим гибањем тијеком аномалије) на секундарној кружној орбити, названој епицикл, који би се и сам кретао једнолико (са средњим гибањем у дужини) дуж главне кружне орбите око Земље, назване деферент; види деферент и епицикл.

Аполоније је демонстрирао да су та два модела заправо математички једнаки. Ипак, све је то била теорија која није била провјерена у пракси. Хипарх је био први који је покушао одредити релативне пропорције и стварне величине тих орбита.

Хипарх је подијелио геометријску методу како би пронашао параметре из 3 положаја Мјесеца у посебним фазама његове аномалије. Уствари, он је то учинио одвојено за ексцентрични модел и модел епицикла.

Птоломеј детаљно описује у Алмагесту IV.11. како је Хипарх користио проматрања два заласка трију помрчина Мјесеца, које је пажљиво одабрао да задовољи увјете. Ексцентрични модел је прилагодио тим помрчинама из својег бабилонског пописа помрчина: 22., 23. просинца 383. пне., 18., 19. липња 382. пне. и 12., 13. просинца 382. пне. Модел епицикла је прилагодио проматрањима мјесечевих помрчина која је направио у Александрији 22. рујна 201. пне., 19. ожујка 200. пне. и 11. рујна 200. пне.

• За ексентрични модел Хипарх је пронашао омјер између полумјера фокуса и удаљености између средишта ексцентричности и средишта еклиптике (тј. проматрача на Земљи): 3144 : 327+2/3;
• а за епициклични модел, омјер између полумјера деферента и епицикла: 3122+1/2 : 247+1/2 .

Ти чудни бројеви су посљедица употребе незграпне јединице коју је користио у својим тригонометријским таблицама. Резултати су видљиво различити. То је дијелом због немарног заокруживања и погрешке у рачунању, због којих га је Птоломеј критизирао (иако је такођер и он сам направио погрешке у заокруживању). Хипарх је ипак пронашао нескладна рјешења. Касније је користио омјер модела епицикла (3122+1/2 : 247+1/2) који је премален (60 : 4;45 хексадецимално): Птоломеј је ставио омјер од 60 : 5+1/4^[6].

Метон, Еуктемон и њихови ученици у Атени су прије Хипарха направили проматрања солстиција (тј. мјерили су тренутак почетка љетног солстиција) 27. липња 432. пне. (пролептички јулијански календар). Аристарх је то направио 280. пне., док је Хипарх имао запис Архимедовог проматрања. Сам је Хипарх проматрао љетни солстициј 135. пне. када је и направио поуздано проматрање почетка еквиноција. Након тог проматрања Хипарх је обавио још многа тијеком свога живота. Птоломеј даје опширно расправљање о Хипарховоме раду о дуљини године у Алмагесту III:1, те наводи многа проматрања која је Хипарх направио и користио, обухваћајући раздобље од 162. пне. до 128. пне.

Птоломеј наводи Хипархово мјерење еквиноција (у зору 24. ожујка 146. пне.) које се разликује од проматрања направљеног тог дана у Александрији (5 сати након изласка сунца). Хипарх је могао посјетити Александрију и обавити своја проматрања еквиноција ондје; али је вјеројатно био на Роду (на истој географској дужини). За та је проматрања могао користити властиту приручну куглу или екваторијални прстен. Хипарх (и Птоломеј) су знали да су проматрања тим инструментима осјетљива на прецизно поравнавање с екватором. Стварни проблем је ипак што атмосферска рефракција значајно подиже Сунце изнад хоризонта, па је његова видљива деклинација превелика, што мијења проматрано вријеме када Сунце прелази екватор. Још горе, рефракција се смањује како се Сунце диже, па се може учинити да се креће у погрешном смјеру у односу на екватор - као што Птоломеј спомиње. Очигледно је да Птоломеј и Хипарх ипак нису схватили да је узрок томе рефракција.

При крају свога дјеловања Хипарх је написао књигу Пери ениаусíоу мегéтхоус ("О дужини године") о својим резултатима. Успостављена вриједност за тропску годину, коју је увео Калип 330. пне. или раније (вјеројатно из бабилонских извора, види горе), била је 365 + 1/4 дана. Хипархово проматрање еквиноција дало је различите резултате, али је он сам истакнуо (наводи се у Алмагесту III.1(Х195)) да погрешке у проматрању од њега и његових претходника не могу бити веће од 1/4 дана. Стога је користио старија проматрања солстиција и одредио разлику од око једног дана у око 300 година. Одредио је дужину тропске године на 365 дана + 1/4 - 1/300 дана (= 365.24666... дана = 365 дана 5 сати 55 мин, која се разликује од стварне дужине (сувремена процјена) од 365.24219... дана = 365 дана 5 сати 48 мин 45 с за око само 6 мин мин).

Између властитог и Метоновог проматрања солстиција, било је 297 година обухваћајући 108478 дана. То подразумијева тропску годину од 365.24579... дана = 365 дана;14,44,51 (сексагезимално; = 365 дана + 14/60 + 44/60² + 51/60³). Та је вриједност пронађена на бабилонској глиненој плочици која је показатељ да је Хипархов рад био познат Калдејцима.

Друга вриједност која се приписује Хипарху (од астролога Веттиуса Валенса у 1. стољећу) је 365 + 1/4 + 1/288 дана (= 365.25347... дана = 36 дана 6 сати 5 мин), али то би могла бити погрешка друге вриједности приписане бабилонским изворима: 365 + 1/4 + 1/144 дана (= 365.25694... дана = 365 дана 6 сати 10 мин). Није јасно да ли би то била вриједност за сидеричку годину (тренутна вриједност у његовом времену (модерна процјена) око 365.2565 дана), али разлика с Хипарховом вриједности за тропску годину је досљедна с његовим трајањем прецесије. (види доље).

Прије Хипарха калдејски астрономи су знали да дужина годишњих доба није једнака. Хипарх је направио проматрања еквиноција и солстиција, па је према Птоломеју (Алмагест III.4) одредио да прољеће (од прољетног еквиноција до љетног солстиција) траје 94 + 1/2 дана, а љето (од љетног солстиција до јесенског еквиноција) 92 + 1/2 дана. То је неочекиван резултат који је добивен под претпоставком гибања Сунца око Земље по кругу једноликом брзином. Хипархово рјешење било је смјестити Земљу не у средиште сунчева гибања, него на некој удаљености од средишта. Тај модел описивао је видљиво кретање Сунца прилично добро (наравно данас се зна да се планети попут Земље крећу по елипсама око Сунца, али то није откривено све док Јоханнес Кеплер није објавио своја прва два закона планетарног гибања 1609.). Вриједност ексентричности коју је Птоломеј приписао Хипарху је да избочени дио износи 1/24 полумјера орбите (што је превелико), а смјер апогеја би био на дужини 65.5° од прољетног еквиноција. Хипарх је могао и употребљавати други дио проматрања (94 + 1/4 и 92 + 3/4 дана), које би довело до различитих вриједности. Остаје питање да ли је Хипарх стваран аутор вриједности које је дао Птоломеј, који није нашао промјене 3 стољећа касније и који је још придодао дужине јесени и зиме.

При побољшавању календара нашао је свој циклус од 4267 мјесеци у лунарном календару с 126.007 + 1/24 дана. То је невјеројатно точан резултат: систематска грешка, одступање почетка попречнога календарскога мјесеца од почетка синодскога мјесеца је само 0,46 секунди мјесечно.

Заједно с Никазом спојио је 476-годишње циклусе с 940 мјесеци и 27.759 дана грчкога астронома Калипа из године 329 пр. Кр. и увео свој 304-годишњи циклус с 3760 мјесеци и 111.035 дана. Његов циклус има врло малу систематску грешку, само - 0,25 секунди мјесечно.

Хипарх се такођер бавио одређивањем удаљености и величине Сунца и Мјесеца. Објавио је своје резултате у дјелу састављеном од двије књиге, а названоме пери мегетхоон каи 'апостèмáтоон ("О величинама и удаљеностима") коју наводи Паппуса у својем коментару на Алмагест V.11; Теон из Смирне (2. стољеће) спомиње назив дјела с додатком "Сунца и Мјесеца".

Хипарх је измјерио видљиве промјере Сунца и Мјесеца својим диоптером. Открио је попут других прије и послије њега да мјесечева величина варира док се креће по својој (ексцентричној) орбити, али није открио ниједну замјетљиву промјену у видљивом промјеру Сунца. Открио је да на средњој удаљености од Мјесеца, Сунце и Мјесец имају једнаки видљиви промјер. На тој удаљености Мјесечев промјер стане 650 пута у круг, тј. средњи видљиви промјери су 360/650 = 0°33'14".

Открио је и да Мјесец има замјетљиву паралаксу, тј. појављује се помакнут од његовог израчунатог положаја (у успоредби са Сунцем и звијездама), а разлика је већа када је ближи хоризонту. Знао је то јер Мјесец кружи око средишта Земље док је проматрач на површини - Мјесец, Земља и проматрач обликују трокут са шиљастим кутом који се мијења цијело вријеме. Из величине те паралаксе, удаљеност Мјесеца се може одредити мјерењем Земљина полумјера. Ипак за Сунце није било никакве видљиве паралаксе (зна се да је она око 8.8", више од 10 пута мања од разлучивости голог ока).

У првој књизи Хипарх закључује да је паралакса Сунца 0, као да је она на бесконачној удаљености. Тада је анализирао помрчину сунца, вјеројатно ону од 14. ожујка 190. пне. То је била потпуна помрчина на подручју Хелеспонта (тиме и у његовом рођеном мјесту Ницеји). У то вријеме Римљани су се спремали за рат с Антиохом III. у том подручју, а помрчину је споменуо и Ливије у својем дјелу Аб Урбе Цондита VIII.2. Помрчина се проматрала и у Александрији гдје је извјештено да је Сунце закривено с 4/5 Мјесеца. Александрија и Ницеја су на истом меридијану док је Александрија на око 31° Н, а подручје Хелеспонта на око 41° Н. Аутори попут Страбона и Птоломеја имали су доста пристојне вриједности за те географске положаје, а вјеројатно их је и Хипарх знао. Хипарх је тако могао нацртати трокут којег су чинила два мјеста и Мјесец. Користивши једноставну геометрију могао је поставити удаљеност до Мјесеца изражену у Земљиним полумјерима. Будући да је помрчина била ујутро, Мјесец није био над меридијаном, па је као посљедица удаљеност коју је израчунао Хипарх била тек доња граница. Било како било, Хипарх је према Паппусу открио да је најмања удаљеност 71 (из те помрчине), а највећа 83 Земљина полумјера.

У другој књизи, Хипарх почиње од супротне претпоставке. Означио је (најмању) удаљеност до Сунца за 470 Земљиних полумјера. То би одговарало паралакси од 7', која је очигледно највећа паралакса за коју је Хипарх мислио да се не може примјетити (за успоредбу: уобичајена разлучивост људског ока је око 2' ; Тyцхо Брахе је направио проматрање голим оком с поузданости до 1'). У том случају, Земљина сјена је стожац више него ваљак као под првом претпоставком. Хипарх је проматрао (тијеком помрчина мјесеца) да на средњој удаљености од Мјесеца, промјер сјене стошца је 2+½ мјесечевих промјера. Тај видљив промјер је, као што је проматрао, 360/650 ступњева. С тим вриједностима и једноставном геометријом, Хипарх је могао одредити средњу удаљеност, јер је израчунато да најмања удаљеност од Сунца је највећа могућа средња удаљеност до Мјесеца. Хипарх је могао са својом вриједности за ексцентричност орбите такођер израчунати најмању и највећу удаљеност од Мјесеца. Према Паппусу, израчунао је најмању удаљеност на 62, средњу на 67+1/3, и према томе највећу удаљеност од 72+2/3 Земљиних промјера. С том методом, док се паралакса Сунца смањује (тј. његова удаљеност повећава), најмања граница за средњу удаљеност је 59 Земљиних промјера - точна средња удаљеност коју је касније Птоломеј извео.

Хипарх је стога имао проблематичне резултате у којима је његова најмања удаљеност (из прве књиге) била већа од његове највеће средње удаљености (из друге књиге). Он је био искрен о том протусловљу, те је вјеројатно схватио да је поготово прва метода осјетљива на поузданост проматрања и параметара (заправо модерна рачунања показују да је величина помрчине Сунца у Александрији морала бити ближе 9/10 него извјештених 4/5).

Птоломеј је касније измјерио изравно мјесечеву паралаксу (Алмагест V.13) и користио је другу Хипархову методу с помрчинама Мјесеца да израчуна удаљеност до Сунца (Алмагест V.15). Критизирао је Хипарха за рађење протусловних претпоставака као и за сакупљање протусловних резултата (Алмагест V.11). Очигледно је погријешио у схваћању Хипархове стратегије да успостави границе досљедне с проматрањима више него иједну вриједност за удаљеност. Његови резултати су били најбољи до тада: садашња средња удаљеност до Мјесеца износи 60.3 Земљиних полумјера, што је у његовим границама из друге књиге.

Теон из Смирне је написао да је према Хипарху Сунце 1880 пута веће од земље, а да је Земља 27 пута већа од мјесечеве величине. Очито се то односило на обујме, а не на промјере. Из геометрије у другој књизи слиједи да је Сунце на удаљености од 2550 Земљиних радијуса, а средња удаљеност до Мјесеца је 60½ полумјера. Слично, Клеомед наводи Хипарха за величине Сунца и Мјесеца као 1050:1 што води до средње мјесечеве удаљености од 61 полумјера Земље. Хипарх је касније очито преправио своје рачуне и извео поуздане појединачне вриједности које је могао користити за предвиђање сунчевих помрчина.

Плиније (Натуралис Хисториа II.X) говори, да је Хипарх показао да се мјесечеве помрчине могу појавити 5 мјесеци одвојено, а сунчеве помрчине 7 мјесеци (умјесто обичних 6 мјесеци). Такођер Сунце може бити скривено двапут у 30 дана, али виђено од различитих народа. Птоломеј расправља потанко о томе стољеће касније у Алмагесту VI. 6. Геометрија и гранични положаји Сунца и Мјесеца у којима је могућа сунчева или мјесечева помрчина објашњени су у Алмагесту VI. 5. Хипарх је вјеројатно учинио слична рачунања. Резултат, да се двије сунчеве помрчине могу појавити одвојено у једном мјесецу је важно, јер се то не може темељити на проматрањима. Једна помрчина је увијек видљива на сјеверној, а друга на јужној полутки, како означује Плиније, а потоња је била недоступна Грцима.

Предвиђање сунчеве помрчине, тј. точно када и гдје ће бити видљива, тражи чврсту лунарну теорију и одговарајуће поступање с мјесечевом паралаксом. Хипарх је засигурно био први, који је успио то направити. Строги поступак тражи сферичну тригонометрију, али то је Хипарх могао направити и с планарном апроксимацијом. Он је могао расправљати о тим стварима у Пери тес ката платос мениаиас тес селенес кинесеоос ("О мјесечном кретању Мјесеца на ширини"), дјело споменуто у Суди.

Плиније такођер означава да "је и он такођер пронашао због којег точног разлога се у прошлости једном догодило да је Мјесец био помрачен на западу, док су и Мјесец и Сунце били видљиви изнад Земље, иако сјена која узрокује помрчину мора бити од изласка сунца па надаље испод Земље." Доказује се, да се то морало односити на огромну потпуну сунчеву помрчину од 26. студеног 139. пне. када је преко чистог морског хоризонта, као што се видјело из града Рода, Мјесец био помрачен на сјеверозападу одмах након сунчевог изласка на југоистоку. То би била друга помрчина у 345-годишњем раздобљу коју је Хипарх користио да потврди традиционална бабилонска раздобља. То ставља касни датум на развој Хипархове лунарне теорије. Не зна се који је "прави разлог" Хипарх пронашао за гледање помрченог Мјесеца док очито није био у правој опозицији према Сунцу. Паралакса спушта висину Сунца и Мјесеца, рефракција их подиже, а с високе точке гледишта хоризонт је спуштен.

Хипарх се приписују изуми или усавршавања неколико астрономских инструмената који су се користили дуго времена у проматрањима голим оком. Према Синезију из Кирене (4. стољеће) Хипарх је направио први астролабион што би могла бити армиларна сфера (за коју Птоломеј ипак каже да ју је он конструирао; Алмагест V.1) или претходник планарних инструмената названих астролаб (којег спомиње Теон из Александрије). С астролабом Хипарх је био први који је могао измјерити географску земљописну ширину и вријеме проматравши звијезде. Прије њега то се радило дању мјерећи бацану сјену гномоном или пријеносним инструментом познат као скафион.

Птоломеј спомиње (Алмагест V.14) да је користио сличан инструмент као и Хипарх, назван диоптра, да измјери видљив промјер Сунца и Мјесеца. Паппус из Александрије га је описао (у коментару на тај одломак из Алмагеста) као и Прокло (Хyпотyпосис IV). Диоптра је била 4-стопе дугачак штап на којем је била означена скала. На једном крају је била рупа кроз коју се гледало и клинасти предмет који се могао мицати дуж штапа како би точно замрачио сунчев или мјесечев диск.

Хипарх је такођер проматрао сунчане еквиноције који су се могли проматрати екваторијалним прстеном. Његова сјена пада на њега када је Сунце изнад екватора (тј. на једној од еквиноцијских точака на еклиптици), али сјена пада изнад или испод насупротне стране прстена када је Сунце јужније или сјеверније од екватора. Птоломеј наводи (у Алмагесту III.1 (Х195)) Хипархов опис екваторијална прстена из Александрије, а мало даље и описује два таква инструмента присутна у Александрији у његово вријеме.

Хипарх је примјенио своје знање сферичних кутова на проблему означавања положаја на Земљиној површини. Прије њега мрежни сустав је користио Дикеарх из Месане, али Хипарх је био први који је примјенио математичку строгост у одређивању ширине и дужине мјеста на Земљи. Хипарх је написао критику у 3 књиге на рад географа Ератостена из Кирене (3. стољеће пне.), названу Прòс тèн 'Ератостхéноус географíан ("Против Ератостенове географије"). То се зна преко Страбона из Амасеје који је у својему осврту критизирао Хипарха у властитој Географији. Хипарх је очито направио много детаљних исправака положаја и удаљености споменутих код Ератостена. Чини се да он није увео многа побољшања у методе, али је предложио начине одређивања географских дужина различитих градова тијеком мјесечевих помрчина (Страбонова Географија 7). Мјесечева помрчина је видљива истодобно на половици Земље, а разлика у дужинама између мјеста може се израчунати из разлике локалних времена проматрања помрчине. Његов приступ би дао поуздане резултате да је точно проведен, али ограничења у поузданости кронометара у његово доба је учинило ту методу непрактичном.

Након тога из 135. пне., занесен око супернове у звијежђу Шкорпиона, измјерио је помоћу екваторијалне армиларне сфере еклиптичне координате од око 1000 звијезда (точан број није познат) за свој звјездани каталог.

Хипарх је такођер знао за дјела Пхаиномена (Појаве). Тј еп, познат као Појаве или Аратеја, описује звијежђе и звијезде које чине то звијежђе. Хипархов коментар садржи многа мјерења положаја звијезда и вријеме изласка, кулминације и заласка звијежђа обрађених у Појавама, и то се вјеројатно темељи на мјерењима звјезданих положаја—и Еноптрон (Огледало природе) од Еудокса из Книда који је имао близу Кизика на јужној обали Мраморног мора властиту школу и кроз Аратову астрономски еп Појаве описује се Еудоксова сфера која је била направљена од метала или камена и на којој су била обиљежена звијежђа, најсјајније звијезде, ракова и јарчева обратница. Ове успоредбе су га осрамотиле јер није могао повезати Еудоксове детаљне тврдње са својим властитим проматрањима и проматрањима тог времена. Из свега тога он је пронашао да су координате звијезда и Сунца биле суставно промијењене. Њихова еклиптична ширина β је остала непромијењена, али њихова еклиптична дужина λ се повећала, за однос за који је процијенио да ће бити најмање 1 ступањ по стољећу.

Тај му је каталог служио да пронађе било какве промјене на небу, али је остао несачуван. Ипак, 2005. је проведена анализа античког кипа Атласа који показује звијезде на положајима за које се чини да су одређене користивши се Хипарховим подацима. [1] Његова звјездана мапа је била у потпуности промијењена 1000 година касније, тј. 964. ју је промијенио Ал Суфи, а 1500 година касније (1437.) Улугх Бег. Касније је Халлеy користио властити звјездани каталог да открије одговарајућа кретања.

Сустав небеских координата који је кориштен у Хипарховом звјезданом каталогу није познат. Од Птоломејеве копије у Алмагесту која је дана у еклиптичним координатама, тај сустав се чини највјеројатнијим, иако постоје докази да су и еклиптичне координате и екваторијалне координате биле кориштене у оригиналним проматрањима.

Хипарх је 130. пне. писао о отвореном јату звијезда, М44 Пресепе (НГЦ 2632) као о "Малом облаку" или "Облачној звијезди". Прије њега објект је био познат Арату око 260. пне., који је писао о њему као о "Маглици". Хипарх је такођер укључио тај предмет у својем славном звјезданом каталогу. Јато звијезда је било такођер познато и кинеским астрономима.

Деламбре у својем дјелу Хистоире де л'Астрономие Анциенне (1817.) закључује да је Хипарх знао и користио реални (небески) екваторијални координатни сустав управо с правим успињањем и опадањем (или с допуном, тј. поларном удаљености). Касније Отто Неугебауер (1899.- 1990.) у својој А Хисторy оф Анциент Матхематицал Астрономy (1975.) одбацује Деламбреове тврдње.

Хипарх је 134. пне. поредао звијезде у шест разреда према порасту њихове величине и сјаја: додао је најсјајнијим звијездама (њих 20) вриједност од 1, слабијима вриједност од 2 и тако даље све до звијезда с разредом 6, које се једва могу видјети голим оком. Тај нацрт је касније прихватио Птоломеј и слични сустави још су увијек у употреби. (Види Привидна магнитуда.)

У додатку својим другим рукописима у којима говори о астрономским темама, Хипархов рад (напредак у другој половици другог стољећа прије Криста) који се бавио рачунањем и предвиђањем небеских положаја би био веома користан онима ангажиранима у облик астрономије познатији као астрологија. Астрологија је развијена у грчко-римском свијету тијеком хеленистичког раздобља посуђујући многе елементе из бабилонске астрономије. Неки повјесничари предлажу да је Хипарх играо кључну улогу у томе. Примједбе која је навео Плиније Старији (умро 79. године након ерупције вулкана Везува), у својој књизи Повијест природе 2. 24, углавном су о неким античким ауторима који су приписивали Хипарху заслугу као важној фигури у повијести астрологије. Плиније тврди да Хипарх неће бити никада довољно похваљен, јер нитко није направио толико као он да докаже да је човјек у односу са звијездама и да наше душе су дио небеса.'

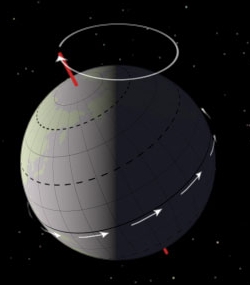
Хипарх је можда најславнији јер је био први који је измјерио прецесију еквиноција. Постоје приједлози да су Бабилонци могли знати о прецесији али чини се да је Хипарх био први који је прецесију уистину разумио и измјерио. Према ал-Баттанију калдејски астрономи су разликовали тропску и сидеричку годину. Он је тврдио да су они око 330. пне. процјенили дужину сидеричке године на С_К = 365 дана 6 сати 11 мин (= 365.258 дана) с погрешком од (око) 2 мин. Тај феномен је био можда познат и Кидиннуу око 314. пне. Први кинески астроном који је споменуо прецесију био је Yу Xи (четврто стољеће).

Хипарх и његови претходници већином су користили једноставне инструменте за астрономско рачунање, као што су гномон, астролаб, армиларна сфера итд.

Као први у повијести Хипарх је исправно објаснио ретроградно кретањем прољетне точке γ над еклиптиком за око 45", 46" или 47" (36" или 3/4' према Птоломеју) годишње (данашња вриједност је 50.29"), те је показао да Земљина ос није непомична у простору. Успоређујући властита мјерења положаја еквиноција са звијездом Спица тијеком мјесечеве помрчине за вријеме еквиноција с онима Еуклидових сувременика (Тимохар из Александрије (око 320. пне.–260. пне.), Аристила 150 година раније, записа калдејских астронома (посебно Кидиннуових записа) и проматрања из храма у Теби у Египату, који је саграђен око 2000. пне.) он је још касније проматрао да се еквиноциј помакнуо за 2° у односу на Спицу. Такођер је примјетио то кретање и на другим звијездама. Узео је вриједност не мању од 1° у стољећу. Модерна вриједност је 1° у 72 године.

Након њега многи грчки и арапски астрономи су потврдили ту појаву. Птоломеј је успоредио свој каталог с онима од Аристила, Тимохара, Хипарха и проматрања Агрипе и Менелаја из Александрије из раног 1. стољећа и напосљетку потврдио Хипархову емпиријску чињеницу да полови небеског екватора у једној Платоновој години (приближно 25,777 сидеричких година) опишу еклиптички пол. Промјер тог круга је једнак нагнутости еклиптике у односу на небески екватор. Еквиноцијске точке у том времену пријеђу цијелу еклиптику и помичу се за 1° по стољећу. Та брзина је једнака оној коју је израчунао Хипарх. Због тих подударности Деламбре, П. Таннерy и други француски повјесничари астрономије су криво закључили да је Птоломеј записао свој звјездани каталог из Хипарховог с правилном екстраполацијом. Није било познато до 1898. када су Марцел Болл и други открили да се Птоломејев каталог разликује од Хипарховог не само у броју звијезда него и у другим аспектима.

Трајање прецесије је било названо по Птоломеју једино зато што прољетна точка γ води Сунце. На латинском праецессе значи "преузети" или "пријећи", и данас такођер значи окретати се и обртати се. Њезино властито име показује да је та појава откривена прије теоретског објашњења, јер би тада добила бољи назив. Многи каснији астрономи, физичари и математичари били су заокупљени тим проблемом, у пракси и теорији. Сама појава је отворила многа нова обећавајућа рјешења у неколико подручја небеске механике: Тхабит ибн Qурраова теорија о вибрацији и осцилацији еквоноцијске точке, Неwтонов опћи закон гравитације (који је у потпуности објаснио), Еулерове кинематичке једнаџбе и Лагрангеове једнаџбе гибања, д'Алембертова динамичка теорија о гибању крутих тијела, те нека алгебарска рјешења за посебне случајеве прецесија, Фламстеедове и Брадлеyеве потешкоће у стварању прецизног телескопског звјезданог каталога, Бесселова и Неwцомбова мјерења прецесије и напокон прецесија перихелија у Еинстеиновој опћој теорији релативности.

Лунисоларна прецесија узрокује да се прољетна точка γ гиба по еклиптици у супротном смјеру од привидног сунчевог гибања и кружења небеског пола. Данашња вриједност износи ψ = 50.388" по години дуж непомичне еклиптике. Тај круг постаје спирала јер други планети поремећују Земљину орбиту. Потоње је планетарна прецесија гдје равнина еклиптике тетура попут зврка (слично лунисоларној прецесији) око непромјенљиве равнине сунчева сустава (стална поред планета попут Јупитера) с квазипериодом од 100,000 година и нагибом који варира између екстрема од 0.1° и 3° (у односу на садашњу еклиптику; нагиб гибања еклиптике досеже 4° у квазипериоду од 60,000 до 70,000 година. Кут између еклиптике и небеског екватора ε = 23° 26' 21.448" постаје мањи за 0.468" годишње. Такођер се точка γ помиче дуж непромјенљива екватора за λ' = 0.1055" годишње у истом смјеру као и Сунце. Зброј тих прецесија даје годишњу опћу прецесију у дужини од п = 50.291" која узрокује да се тропска година разликује од сидеричке године. Те вриједности су прихваћене од Међународне Астрономске Уније 1976. за подне 1. сијечња 2000. (Ј2000.0) — вриједности за 1900. или 1950. још се увијек налазе у многим енциклопедијама.

• Магнитуда (астрономија)
• Астрометрија
• Повијест астрологије
• Гемин (с Рода) (10. пне. - око 60.)
• Мира
• Митраизам
• Звјездани каталози