Base (álgebra linear)

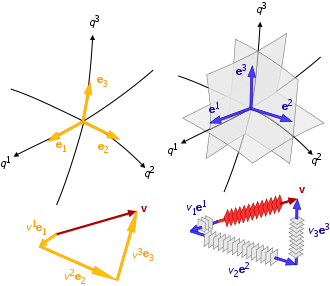
Na álgebra linear, uma base de um espaço vectorial é um conjunto de vetores linearmente independentes que geram esse espaço.^[1]

Se ${\displaystyle E}$ é um espaço vectorial sobre um corpo ${\displaystyle K,}$ chama-se base de ${\displaystyle E}$ a um conjunto de vectores de ${\displaystyle E}$ linearmente independentes que gera ${\displaystyle E.}$

• O espaço vectorial ${\displaystyle \mathbb {R} ^{n}}$ tem por base o conjunto^[2]

${\displaystyle \{(1,0,0,\ldots ,0,0),(0,1,0,\ldots ,0,0),\ldots ,(0,0,0,\ldots ,0,1)\},}$

que se denomina a sua base canónica.

• No plano ${\displaystyle \mathbb {R} ^{2},}$ a recta de equação ${\displaystyle y=mx}$ tem por base o conjunto ${\displaystyle \{(1,m)\}.}$
• O espaço vectorial dos polinómios p(x) de coeficientes reais tem uma base infinita, o conjunto ${\displaystyle \{1,x,x^{2},x^{3},\ldots \}.}$
• Cada corpo K pode ser considerado como um espaço vectorial sobre ele mesmo. Neste caso, qualquer elemento não-nulo ${\displaystyle a}$ forma uma base ${\displaystyle \{a\}.}$
• O espaço vectorial formado pelo vetor nulo ${\displaystyle \{0\}}$ tem como base o conjunto vazio.^[2]
• Seja ${\displaystyle \alpha \in L}$ um elemento algébrico sobre o corpo ${\displaystyle K,}$ sendo ${\displaystyle L}$ uma extensão de ${\displaystyle K.}$ Então existe um polinômio ${\displaystyle p(x)}$ com coeficientes em ${\displaystyle K}$ tal que ${\displaystyle p(x)=0.}$ Podemos definir ${\displaystyle n,}$ o grau de ${\displaystyle \alpha }$ em ${\displaystyle K,}$ como o menor grau dos polinômios ${\displaystyle p(x)}$ em que ${\displaystyle p(x)=0.}$ Então ${\displaystyle K[\alpha ]}$ é uma extensão algébrica de ${\displaystyle K}$ e, portanto, podemos considerar ${\displaystyle K[\alpha ]}$ como um espaço vetorial sobre ${\displaystyle K.}$ Neste caso, a sua base é ${\displaystyle \{1,\alpha ,\ldots ,\alpha ^{n-1}\}.}$

Um espaço vectorial pode ter mais de uma base. De facto, um espaço vectorial só pode ter uma única base nos seguintes casos:

• o espaço formado só por ${\displaystyle 0}$ sobre qualquer corpo (a base é o conjunto vazio);
• o espaço ${\displaystyle \mathbb {Z} _{2}}$ como espaço vectorial sobre o corpo ${\displaystyle \mathbb {Z} _{2}}$ (a base é {${\displaystyle 1}$}).

Os seguintes resultados, porém, são válidos:

• Se um espaço vectorial tem uma base ${\displaystyle B}$ finita, então todas as outras bases também são finitas, e têm a mesma cardinalidade.^[3]
• De modo geral, supondo-se o axioma da escolha, duas bases de um espaço vectorial ${\displaystyle V}$ tem a mesma cardinalidade (mesmo se a base for um conjunto infinito). Esta cardinalidade designa-se por dimensão de ${\displaystyle V.}$^[4] Um espaço vectorial que possui uma de suas bases formada por 3 vectores, por exemplo, é um espaço vetorial de dimensão 3.

Usando-se uma forma equivalente do axioma da escolha, o Lema de Zorn, é fácil mostrar que todo espaço vectorial ${\displaystyle V}$ tem uma base e, mais geralmente, provar que, para qualquer conjunto ${\displaystyle S}$ linearmente independente de vectores de ${\displaystyle V,}$ existe uma base ${\displaystyle B}$ de ${\displaystyle V}$ que contém ${\displaystyle S.}$ Seja ${\displaystyle L}$ o conjunto de todos as partes linearmente independentes de ${\displaystyle V}$ que contêm ${\displaystyle S.}$ O conjunto ${\displaystyle L}$ está parcialmente ordenado pela inclusão de conjuntos. Seja ${\displaystyle F}$ uma parte de ${\displaystyle L}$ totalmente ordenada. Então ${\displaystyle F}$ é majorado; basta ver que a união de todos os elementos de ${\displaystyle F}$ é novamente linearmente independente e contém ${\displaystyle S}$ (ou seja, pertence a ${\displaystyle L}$) e que contém todos os elementos de ${\displaystyle F.}$ O lema de Zorn afirma então que ${\displaystyle L}$ tem algum elemento maximal ${\displaystyle B.}$ Então, como ${\displaystyle B}$ ∈ ${\displaystyle L,}$ ${\displaystyle B}$ é linearmente independente e contém ${\displaystyle S.}$ Se ${\displaystyle B}$ não gerasse ${\displaystyle V,}$ haveria algum vector ${\displaystyle v}$ ∈ ${\displaystyle V}$ que não seria combinação linear de elementos de ${\displaystyle B.}$ Então ${\displaystyle B}$ ∪ ${\displaystyle \{v\}}$ seria também um conjunto linearmente independente que conteria ${\displaystyle S.}$ Mas ${\displaystyle B}$ ⊂ ${\displaystyle B}$ ∪ ${\displaystyle \{v\}}$ e ${\displaystyle B}$ ≠ ${\displaystyle B}$ ∪ ${\displaystyle \{v\},}$ o que está em contradição com ${\displaystyle B}$ ser um elemento maximal de ${\displaystyle L.}$ Logo, ${\displaystyle B}$ gera ${\displaystyle V}$ e, portanto, é uma base.

Se o espaço vectorial ${\displaystyle V}$ tem uma base ${\displaystyle B,}$ e ${\displaystyle W}$ é um subespaço vectorial de ${\displaystyle V,}$ então ${\displaystyle W}$ tem uma base ${\displaystyle B_{1}}$ com as seguintes propriedades:

• Se ${\displaystyle B}$ é um conjunto finito e ${\displaystyle W}$ é um subconjunto próprio de ${\displaystyle V,}$ então ${\displaystyle B_{1}}$ tem menos elementos que ${\displaystyle B.}$
• No caso geral, pode-se apenas afirmar que a cardinalidade de ${\displaystyle B_{1}}$ é menor ou igual que a de ${\displaystyle B.}$

Outra propriedade importante é a seguinte:

• Se W é um subespaço vectorial de V, e W tem uma base B₁, então existe uma base B de V tal que B₁ é um subconjunto de B.

Este resultado, no caso infinito, depende do axioma da escolha.

Uma boa forma de interpretar o conceito de Base é pensar nas cores primárias: se misturarmos amarelo, magenta e azul ciano nas proporções correctas podemos criar qualquer outra cor que desejemos. Além do mais, tal proporção é única para a cor desejada. Da mesma forma, uma Base permite-nos, de maneira única, combinar linearmente ("misturar") os seus vectores ("cores primárias") para obtermos o vector ("a cor") que pretendemos.

• Callioli, Carlos A.; Hygino H. Domingues; Roberto C. F. Costa (1990). Álgebra Linear e Aplicações 6 ed. São Paulo: Atual. ISBN 9788570562975  A referência emprega parâmetros obsoletos |coautor= (ajuda)

• Bases, subespaços e somas diretas (exemplo) - Lima, L. Elon.