Icosahedrale symmetrie

Icosahedrale symmetrie is de symmetrie van verschillende regelmatige veelvlakken, dus een vorm van polyhedrale symmetrie. Icosahedraal wordt ook geschreven als icosaedraal of als icosaedrisch, al of niet met trema.

Er zijn twee vormen van icosahedrale symmetrie, maar het gaat in beide gevallen om polyhedrale symmetrie.

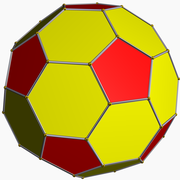
• Volledige icosahedrale symmetrie is de symmetrie van onder meer het regelmatige twaalfvlak of dodecaëder, het regelmatige twintigvlak of icosaëder en de als voetbal zeer bekende afgeknotte icosaëder.
• Chirale icosahedrale symmetrie is de symmetrie van onder meer de stompe dodecaëder en de vijfhoekige hexacontaëder. Deze twee lichamen zijn elkaars duale veelvlak. Er komen van beide lichamen twee chirale vormen voor, dus twee verschillende lichamen die wel elkaars spiegelbeeld zijn, maar niet gelijk aan hun eigen spiegelbeeld.

Volledige icosahedrale symmetrie is met spiegeling en heeft symmetriegroep ${\displaystyle I_{h}}$ van orde 120. Chirale icosahedrale symmetrie is zonder spiegeling en heeft symmetriegroep ${\displaystyle I}$ van orde 60.

Beide symmetriegroepen hebben de volgende assen van rotatiesymmetrie met het volgende aantal punten waar ze het oppervlak van een convex object met icosahedrale symmetrie snijden (het aantal assen is steeds de helft):

• 12 van orde 5. Ze gaan in de voorbeelden door de middens van vijfhoeken en tienhoeken, en door hoekpunten waar 5 gelijke hoeken samenkomen.
• 20 van orde 3. Ze gaan in de voorbeelden door de middens van driehoeken en zeshoeken, en door hoekpunten waar 3 gelijke hoeken samenkomen.
• 30 van orde 2. Ze gaan in de voorbeelden door de middens van ribben waar twee gelijke zijvlakken aan elkaar grenzen, de middens van zijvlakken die regelmatige veelhoeken met een even aantal hoeken zijn, de middens van ruiten, en hoekpunten waar vier gelijke hoeken samenkomen.

Het aantal maal de orde is steeds 60, de orde van ${\displaystyle I}$.

De volledige versie heeft verder 15 spiegelvlakken. In termen van de orde van de gepasseerde rotatiepunten volgen de corresponderende grote cirkels de cyclus (525323), twee cycli voor een grote cirkel. Ze gaan gezamenlijk door alle rotatiepunten, en wel zovaak als de orde is. De spiegelvlakken gaan in de voorbeelden loodrecht door de middens van ribben, langs ribben en door hoekpunten. Het fundamenteel domein is de driehoek 235, 1/120 deel van het veelvlak. Het bekijken van het fundamenteel domein kan het overzichtelijker maken om figuren met een bepaalde symmetrie te onderscheiden en vergelijken.

${\displaystyle I}$ is algebraïsch de alternerende groep ${\displaystyle A_{5}}$, de even permutaties van 5 elementen. De 20 hoekpunten van een twaalfvlak kunnen namelijk, op twee manieren, over 5 groepen van 4 worden verdeeld, die elk de hoekpunten vormen van een viervlak. De elementen van ${\displaystyle I}$ corresponderen 1-op-1 met de even permutaties van de 5 tetraëders. ${\displaystyle I_{h}}$ = ${\displaystyle I}$ ${\displaystyle \oplus }$ C_i, dus algebraïsch A₅ × C₂.

Tetrahedrale en octahedrale symmetrie zijn twee andere vormen van polyhedrale symmetrie. Alle zijvlakken van de hier behandelde veelvlakken zijn regelmatige veelhoeken.

Er zijn twee regelmatige veelvlakken met volledige icosahedrale symmetrie:^[1]

• 
  twaalfvlak
• 
  twintigvlak

Nederlandse naam	Griekse naam	Afbeelding	Hoekpunten per vlak	Vlakken per hoekpunt	Vlakken	Ribben	Hoekpunten	Schläfli-symbool	Symmetriegroep
regelmatig twaalfvlak	dodecaëder		5	3	12	30	20	{5, 3}	${\displaystyle I_{h}}$
regelmatig twintigvlak	icosaëder		3	5	20	30	12	{3, 5}	${\displaystyle I_{h}}$

Er zijn vijf archimedische lichamen met volledige icosahedrale symmetrie. De bolvormige variant van de afgeknotte icosaëder is zeer bekend als voetbal.

Naam (hoekpuntconfiguratie)	Afbeelding	Openvouwing	Vlakken	Soort vlakken	Ribben	Hoekpunten	Symmetriegroep
icosidodecaëder (3.5.3.5)	(Animatie)		32	20 driehoeken 12 vijfhoeken	60 tussen een driehoek en een vijfhoek; het veelvlak is quasiregelmatig, dat wil zeggen dat het ook ribbetransitief is	30	${\displaystyle I_{h}}$
afgeknotte dodecaëder (3.10.10)	(Animatie)		32	20 driehoeken 12 tienhoeken	90 (60 tussen een driehoek en een tienhoek en 30 tussen een twee tienhoeken)	60	${\displaystyle I_{h}}$
afgeknotte icosaëder (5.6.6)	(Animatie)		32	12 vijfhoeken 20 zeshoeken	90 (60 tussen een vijfhoek en een zeshoek en 30 tussen een twee zeshoeken)	60	${\displaystyle I_{h}}$
rombische icosidodecaëder of kleine rombische icosidodecaëder (3.4.5.4)	(Animatie)		62	20 driehoeken 30 vierkanten 12 vijfhoeken	120 (60 tussen een vierhoek en een vijfhoek en 60 tussen een driehoek en een vierkant)	60	${\displaystyle I_{h}}$
afgeknotte icosidodecaëder of grote rombische icosidodecaëder (4.6.10)	(Animatie)		62	30 vierkanten 20 zeshoeken 12 tienhoeken	180 (60 tussen een tienhoek en een zeshoek, 60 tussen een tienhoek en een vierkant, en 60 tussen een vierkant en een driehoek)	120	${\displaystyle I_{h}}$

Een aanduiding als 3.5.3.5 (hoekpuntconfiguratie) geeft in volgorde aan welke regelmatige veelhoeken bij elk hoekpunt samenkomen.

De laatste, met de meeste hoekpunten, heeft de bijzonderheid dat dit aantal gelijk is aan de orde van de symmetriegroep. Er is dus geen niet-triviale isometrie die een hoekpunt op zichzelf afbeeldt. De assen en spiegelvlakken gaan dus niet door hoekpunten. Het is dan ook de enige van de vijf veelvlakken met een hoekpuntconfiguratie waarvan de cyclus in omgekeerde richting anders is.

Er zijn vijf catalanlichamen met volledige icosahedrale symmetrie.

naam	afbeelding	archimedisch lichaam	openvouwing	vlakken	ribben	hoekpunten	symmetriegroep
rombische triacontaëder	Animatie	icosidodecaëder		30 ruiten V3.5.3.5	60 het veelvlak is ribbetransitief	32	${\displaystyle I_{h}}$
driehoekige icosaëder	Animatie	afgeknotte dodecaëder		60 gelijkbenige driehoeken V3.10.10	90 (30 lange en 60 korte)	32	${\displaystyle I_{h}}$
pentakische dodecaëder	Animatie	afgeknotte icosaëder		60 gelijkbenige driehoeken V5.6.6	90 waarvan 30 iets langer dan de andere	32	${\displaystyle I_{h}}$
deltaëdrische hexacontaëder	Animatie	rombische icosidodecaëder		60 vliegers V3.4.5.4	120 (60 lange en 60 korte)	62	${\displaystyle I_{h}}$
disdyakische triacontaëder	Animatie	afgeknotte icosidodecaëder		120 bijna rechthoekige driehoeken V4.6.10	180 (60 lange, 60 middellange en 60 korte)	62	${\displaystyle I_{h}}$

Een aanduiding als V3.5.3.5 geeft voor elke hoek van de veelhoek aan hoeveel daarvan samenkomen. De hoeken in het corresponderende bolvormige veelvlak zijn 360° gedeeld door het getal, de hoeken van de vlakke veelhoek zijn iets kleiner.

• 
  cI (4e) *
• 
  dakD (6e) *
• 
  atD (6e)
• 
  atI=akD (6e) *
• 
  qD (6e)
• 
  m3D (6e)
• 
  m3I (6e)
• 
  b3D (6e)
• 
  b3I (6e)
• 
  edaD (8e) *
• 
  gaD (10e)
• 
  XI (10e)
• 
  XD (10e)
• 
  dXI (10e)
• 
  dXD (10e)
• 
  teD (12e) *
• 
  m3aI (12e)
• 
  tatI = takD (18e)
• 
  tatD (18e)
• 
  atkD (18e)
• 
  m3tD (18e)
• 
  dqtI = k5k6etI (18e)
• 
  qtI = t5t6otI (18e)
• 
  actI (24e)

Constructie van {3,5+}6,0 uit {3,5+}1,0 Constructie van {3,5+}3,3 uit {5+,3}1,0 via {3,5+}1,1

Geodetische veelvlakken met volledige icosahedrale symmetrie worden aangeduid als {3,5+}_m,n met gehele getallen ${\displaystyle m}$ en ${\displaystyle n}$, en ${\displaystyle m>0}$, en ${\displaystyle n=0}$ (klasse I) of ${\displaystyle n=m}$ (klasse II). ${\displaystyle T}$ is het triangulatiegetal, gegeven door ${\displaystyle T=m^{2}+mn+n^{2}}$, dus respectievelijk ${\displaystyle T=m^{2}}$ en ${\displaystyle T=3m^{2}}$. Ze kunnen worden geconstrueerd als in de figuur.

{3,5+}_m,0 heeft ${\displaystyle 10T+2=10m^{2}+2}$ hoekpunten, ${\displaystyle 30T=30m^{2}}$ ribben en ${\displaystyle 20T=20m^{2}}$ zijvlakken.

{3,5+}_m,m heeft ${\displaystyle 10T+2=30m^{2}+6}$ hoekpunten, ${\displaystyle 30T=90m^{2}}$ ribben en ${\displaystyle 20T=60m^{2}}$ zijvlakken.

Bij de geodetische veelvlakken in klasse ${\displaystyle I}$ bestaat de verbindingslijn tussen twee nabije 5-valente hoekpunten uit ${\displaystyle m}$ ribben. In klasse II bevinden zich er ${\displaystyle 2m}$ driehoeken tussen. ${\displaystyle T}$ geeft aan met welke factor het aantal driehoeken wordt vermenigvuldigd ten opzichte van dat van het regelmatig twaalfvlak.

Er bestaan eenduidige duale versies hiervan, de goldbergveelvlakken, met vlakke zijvlakken en behoud van symmetrie.^[2] Ze worden aangeduid als {5+,3}_m,n.

Er geldt dus:

{5+,3}_m,0 heeft ${\displaystyle 10T+2=10m^{2}+2}$ zijvlakken, ${\displaystyle 30T=30m^{2}}$ ribben en ${\displaystyle 20T=20m^{2}}$ hoekpunten.

{5+,3}_m,m heeft ${\displaystyle 10T+2=30m^{2}+6}$ zijvlakken, ${\displaystyle 30T=90m^{2}}$ ribben en ${\displaystyle 20T=60m^{2}}$ hoekpunten.

Twee nabije vijfhoeken hebben bij de goldbergveelvlakken in klasse ${\displaystyle I}$ hun zijden naar elkaar gekeerd, en ertussen bevinden zich ${\displaystyle m-1}$ zeshoeken. Nabije vijfhoeken in klasse II hebben hun hoeken naar elkaar gekeerd, en er zijn langs de verbindingslijn ${\displaystyle m}$ ribben en ${\displaystyle m-1}$ zeshoeken, om en om.

{5+,3}_1,0 is een regelmatig veelvlak en {5+,3}_1,1 een archimedisch lichaam, de zeshoeken zijn dus regelmatig. Bij de overige goldbergveelvlakken zijn alle zeshoeken of een deel ervan onregelmatig: de zijden zijn wel even lang, maar de hoeken zijn niet gelijk. Zo heeft bijvoorbeeld {5+,3}_2,0 zeshoeken met twee hoeken van 116,6°, die waar drie zeshoeken samenkomen, en vier van 121,7°.^[3]

Uit {3,5+}_m,0 wordt {3,5+}_km,0 geconstrueerd volgens de eerste rij afbeeldingen. Uit {3,5+}_m,m wordt dit {3,5+}_km,km. Uit {5+,3}_m,0 wordt {3,5+}_m,m geconstrueerd door 12 vijfhoeken te verdelen in elk vijf driehoeken en ${\displaystyle 10(m^{2}-1)}$ zeshoeken in elk zes driehoeken, zodat er ${\displaystyle 60m^{2}}$ driehoeken ontstaan. Uit {5+,3}_m,m ontstaat zo {3,5+}_2m,0.

Hieronder volgt een tabel met geselecteerde geodetische veelvlakken en bijbehorende goldbergveelvlakken met volledige icosahedrale symmetrie. De kolom Zijvlakkendriehoek geeft voor de geodetische veelvlakken de zijvlakken aan tussen drie nabije 5-valente hoekpunten. Voor de goldbergveelvlakken geven de hoekpunten van de gelijkzijdige driehoeken in de figuur de zijvlakken aan tussen (en inclusief) drie nabije vijfhoeken.

m	n	${\displaystyle T}$	Klasse	Hoekpunten (geodetisch) Zijvlakken (goldberg) ${\displaystyle 10\ T+2}$	Ribben ${\displaystyle 30\ T}$	Zijvlakken (geodetisch) Hoekpunten (goldberg) ${\displaystyle 20\ T}$	Zijvlakken- driehoek	Geodetisch			Goldberg
								Symbolen	Conway	Afbeelding	Symbolen	Conway	Afbeelding
1	0	1	I	12	30	20		{3,5} {3,5+}1,0	I		{5,3} {5+,3}1,0 GP5(1,0)	D
2	0	4	I	42	120	80		{3,5+}2,0	uI dcdI		{5+,3}2,0 GP5(2,0)	cD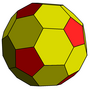
3	0	9	I	92	270	180		{3,5+}3,0	xI ktI		{5+,3}3,0 GP5(3,0)	yD tkD
4	0	16	I	162	480	320		{3,5+}4,0	uuI dccD		{5+,3}4,0 GP5(4,0)	c2D
5	0	25	I	252	750	500		{3,5+}5,0	u5I u5I		{5+,3}5,0 GP5(5,0)	c5D
6	0	36	I	362	1080	720		{3,5+}6,0	uxI dctkdI		{5+,3}6,0 GP5(6,0)	cyD ctkD
7	0	49	I	492	1470	980		{3,5+}7,0	vvI dwrwdI		{5+,3}7,0 GP5(7,0)	wwD wrwD
8	0	64	I	642	1920	1280		{3,5+}8,0	u3I dcccdI		{5+,3}8,0 GP5(8,0)	cccD
9	0	81	I	812	2430	1620		{3,5+}9,0	xxI ktktI		{5+,3}9,0 GP5(9,0)	yyD tktkD
10	0	100	I	1002	3000	2000		{3,5+}10,0	uu5I uu5I		{5+,3}10,0 GP5(10,0)	cc5D
11	0	121	I	1212	3630	2420		{3,5+}11,0	u11I u11I		{5+,3}11,0 GP5(11,0)	c11D
12	0	144	I	1442	4320	2880		{3,5+}12,0	uuxD dcctkD		{5+,3}12,0 GP5(12,0)	ccyD cctkD
13	0	169	I	1692	5070	3380		{3,5+}13,0	u13I u13I		{5+,3}13,0 GP5(13,0)	c13D
14	0	196	I	1962	5880	3920		{3,5+}14,0	uvvI dcwwdI		{5+,3}14,0 GP5(14,0)	cwrwD
15	0	225	I	2252	6750	4500		{3,5+}15,0	u5xI u5ktI		{5+,3}15,0 GP5(15,0)	c5yD c5tkD
16	0	256	I	2562	7680	5120		{3,5+}16,0	dc4dI		{5+,3}16,0 GP5(16,0)	ccccD
1	1	3	II	32	90	60		{3,5+}1,1	kD		{5+,3}1,1 GP5(1,1)	yD ktD
2	2	12	II	122	360	240		{3,5+}2,2	unI =dctI		{5+,3}2,2 GP5(2,2)	czD cdkD
3	3	27	II	272	810	540		{3,5+}3,3	xnI ktkD		{5+,3}3,3 GP5(3,3)	yzD tkdkD
4	4	48	II	482	1440	960		{3,5+}4,4	u2nI dcctI		{5+,3}4,4 GP5(4,4)	c2zD cctI
5	5	75	II	752	2250	1500		{3,5+}5,5	u5nI		{5+,3}5,5 GP5(5,5)	c5zD
6	6	108	II	1082	3240	2160		{3,5+}6,6	uxnI dctktI		{5+,3}6,6 GP5(6,6)	cyzD ctkdkD
7	7	147	II	1472	4410	2940		{3,5+}7,7	vvnI dwrwtI		{5+,3}7,7 GP5(7,7)	wwzD wrwdkD
8	8	192	II	1922	5760	3840		{3,5+}8,8	u3nI dccckD		{5+,3}8,8 GP5(8,8)	c3zD ccctI
9	9	243	II	2432	7290	4860		{3,5+}9,9	xxnI ktktkD		{5+,3}9,9 GP5(9,9)	yyzD tktktI
12	12	432	II	4322	12960	8640		{3,5+}12,12	uuxnI dccdktkD		{5+,3}12,12 GP5(12,12)	ccyzD cckttI
14	14	588	II	5882	17640	11760		{3,5+}14,14	uvvnI dcwwkD		{5+,3}14,14 GP5(14,14)	cwwzD cwrwtI
16	16	768	II	7682	23040	15360		{3,5+}16,16	uuuunI dcccctI		{5+,3}16,16 GP5(16,16)	cccczD cccctI

• 
  regelmatig twaalfvlak
  {5+,3}_1,0
• 
  dkD=tI (3e) *
  afgeknotte icosaëder
  {5+,3}_1,1
• 
  t5daD=cD (4e) *
  ribbe-afgeknotte dodecaëder
  {5+,3}_2,0
• 
  tkdD (9e) *
  afgeknotte pentakisdodecaëder
  {5+,3}_3,0
• 
  cdkD (12e)
  ribbe-afgeknotte afgeknotte icosaëder
  {5+,3}_2,2
• 
  tktI (27e)
  {5+,3}_3,3
• 
  ctkD (36e)
  {5+,3}_6,0

Het fundamenteel domein is de driehoek tussen nabije assen met orde 2, 3 en 5, dit is 1/120 deel van het veelvlak. Als illustratie van het bepalen van het aantal zijvlakken enz. door die in het fundamenteel domein te tellen (ook bij andere veelvlakken met volledige icosahedrale symmetrie) wordt dit hier gedaan bij de afgebeelde selectie goldbergveelvlakken.

Het fundamenteel domein bevat altijd 1/10 vijfhoek, en verder:

bij een regelmatig twaalfvlak niets, bij een afgeknotte icosaëder een vliegervormige 1/6 zeshoek, bij een ribbe-afgeknotte dodecaëder 1/4 zeshoek, bij een afgeknotte pentakisdodecaëder een vijfhoekige 1/2 zeshoek en een driehoekige 1/6 zeshoek, bij een ribbe-afgeknotte afgeknotte icosaëder een vijfhoekige 1/2 zeshoek, 1/4 zeshoek en een driehoekige 1/6 zeshoek, bij tktI vier vijfhoekige halve zeshoeken en een vliegervormige 1/6 zeshoek, bij ctkD een hele zeshoek, drie vijfhoekige halve zeshoeken, 1/4 zeshoek en een vliegervormige 1/6 zeshoek. Het hele veelvlak heeft dus steeds 12 vijfhoeken en resp. 0, 20, 30, 80, 110, 260 en 350 zeshoeken.

Op dezelfde manier kan het aantal hoekpunten bepaald worden, maar dan telt een hoekpunt wel slechts mee voor een gedeelte dat correspondeert met het aantal exemplaren van het fundamenteel domein waar het aan grenst (1, 2, 4, 6 of 10). Zo gerekend is het aantal hoekpunten in het fundamenteel domein resp. 1/6, 1/2, 2/3, 1 1/2, 2, 4 1/2 en 6, en in totaal dus resp. 20, 60, 80, 180, 240, 540 en 720. Evenzo telt bij het bepalen van het aantal ribben in het fundamenteel domein een gedeeltelijk ribbe slechts voor dat deel, en bovendien gehalveerd als deze langs de rand van het fundamenteel domein loopt. De formule van Euler voor veelvlakken kan worden gebruikt om de berekeningen te beperken of te controleren. Een en ander gaat analoog bij een andere symmetrie.

Recapitulerend ter vergelijking:

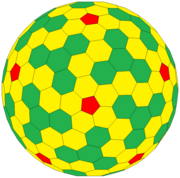
Bij {5+,3}_m,0 hebben twee nabije vijfhoeken hun zijden naar elkaar gekeerd, en bevinden zich er ${\displaystyle m-1}$ zeshoeken tussen. Het heeft 12 vijfhoeken en ${\displaystyle 10(m^{2}-1)}$ zeshoeken, ${\displaystyle 30m^{2}}$ ribben en ${\displaystyle 20m^{2}}$ hoekpunten.

Bij {5+,3}_m,m hebben nabije vijfhoeken hun hoeken naar elkaar gekeerd, en zijn er langs de verbindingslijn ${\displaystyle m}$ ribben en ${\displaystyle m-1}$ zeshoeken. Het heeft 12 vijfhoeken en ${\displaystyle 10(3m^{2}-1)}$ zeshoeken, ${\displaystyle 90m^{2}}$ ribben en ${\displaystyle 60m^{2}}$ hoekpunten.

Als bij de afgebeelde figuur met volledige icosahedrale symmetrie lijnen slechts worden opgevat als verdeling in de 120 fundamentele domeinen dan zijn er per stuk 1/10 tienhoek en 1/6 zeshoek, als het ribben zijn dan zijn er per fundamenteel domein een rode en een gele driehoek. Het hele oppervlak heeft dus respectievelijk 12 tienhoeken en 20 zeshoeken (gekromd) of 120 rode en 120 gele driehoeken. Per fundamenteel domein zijn er respectievelijk 1 en 3 ribben, dus in totaal respectievelijk 120 en 360. Per fundamenteel domein zijn er respectievelijk 3/4 en 61/60 hoekpunten, dus in totaal respectievelijk 90 en 122.

Er zijn twee archimedische lichamen met chirale icosahedrale symmetrie. Ze zijn elkaars spiegelbeeld.

Naam (hoekpuntconfiguratie)	Afbeelding	Openvouwing	Vlakken	Soort vlakken	Ribben	Hoekpunten	Symmetriegroep
stompe dodecaëder of afgeknotte icosidodecaëder (2 chirale vormen) (3.3.3.3.5)	(Animatie) (Animatie)		92	80 driehoeken 12 vijfhoeken	150	60	${\displaystyle I}$

Er zijn twee catalanlichamen met chirale icosahedrale symmetrie. Ze zijn elkaars spiegelbeeld. Hieronder wordt er één getoond.

naam	afbeelding	archimedisch lichaam	openvouwing	vlakken	ribben	hoekpunten	symmetriegroep
vijfhoekige hexacontaëder	Animatie	stompe dodecaëder		60 vliegerachtige spiegelsymmetrische vijfhoeken met 4 gelijke hoeken V3.3.3.3.5	150 (60 lange en 90 korte)	92	${\displaystyle I}$

• 
  dsD (5e)
• 
  sD (5e)
• 
  wD (7e)
• 
  k5sD (7e)
• 
  saD (10e)
• 
  saD (10e)
• 
  g3D (11e)
• 
  s3D (11e)
• 
  g3I (11e)
• 
  s3I (11e)
• 
  stI (15e)
• 
  stD (15e)
• 
  wtI (21e)
• 
  k5k6stI (21e)

Geodetische veelvlakken met chirale icosahedrale symmetrie worden aangeduid als {3,5+}_m,n en {5+,3}_m,n met gehele getallen ${\displaystyle m,n\geq 1}$, en ${\displaystyle m\neq n}$ (klasse III). Verwisselen van ${\displaystyle m}$ en ${\displaystyle n}$ geeft de gespiegelde versie. ${\displaystyle T}$ is het triangulatiegetal, gegeven door ${\displaystyle T=m^{2}+mn+n^{2}}$.

Er bestaan eenduidige duale versies hiervan, de goldbergveelvlakken, met vlakke zijvlakken en behoud van symmetrie.^[2] Ze worden aangeduid als {5+,3}_m,n.

Bij de goldbergveelvlakken zijn alle zeshoeken of een deel ervan onregelmatig: de zijden zijn wel even lang, maar de hoeken zijn niet gelijk.

Hieronder volgt een tabel met geselecteerde geodetische veelvlakken en bijbehorende goldbergveelvlakken met chirale icosahedrale symmetrie, met van enantiomorfe paren steeds maar een van de twee, met ${\displaystyle m>n}$. De kolom Zijvlakkendriehoek geeft voor de geodetische veelvlakken de zijvlakken aan tussen drie nabije 5-valente hoekpunten. Voor de goldbergveelvlakken geven de hoekpunten van de gelijkzijdige driehoeken in de figuur de zijvlakken aan tussen (en inclusief) drie nabije vijfhoeken.

m	n	${\displaystyle T}$	Klasse	Hoekpunten (geodetisch) Zijvlakken (goldberg) ${\displaystyle 10\ T+2}$	Ribben ${\displaystyle 30\ T}$	Zijvlakken (geodetisch) Hoekpunten (goldberg) ${\displaystyle 20\ T}$	Zijvlakken- driehoek	Geodetisch			Goldberg
								Symbolen	Conway	Afbeelding	Symbolen	Conway	Afbeelding
2	1	7	III	72	210	140		{3,5+}2,1	vI dwD		{5+,3}2,1 GP5(2,1)	wD
3	1	13	III	132	390	260		{3,5+}3,1	v3,1I		{5+,3}3,1 GP5(3,1)	w3,1D
3	2	19	III	192	570	380		{3,5+}3,2	v3I		{5+,3}3,2 GP5(3,2)	w3D
4	1	21	III	212	630	420		{3,5+}4,1	dwtI		{5+,3}4,1 GP5(4,1)	wkI
4	2	28	III	282	840	560		{3,5+}4,2	vnI dwtI		{5+,3}4,2 GP5(4,2)	wdkD
4	3	37	III	372	1110	740		{3,5+}4,3	v4I		{5+,3}4,3 GP5(4,3)	w4D
5	1	31	III	312	930	620		{3,5+}5,1	u5,1I		{5+,3}5,1 GP5(5,1)	w5,1D
5	2	39	III	392	1170	780		{3,5+}5,1	u5,1I		{5+,3}5,1 GP5(5,1)	w5,1D
5	3	49	III	492	1470	980		{3,5+}5,3	vvI dwwD		{5+,3}5,3 GP5(5,3)	wwD
6	2	52	III	522	1560	1040		{3,5+}6,2	v3,1uI		{5+,3}6,2 GP5(6,3)	w3,1cD
6	3	63	III	632	1890	1260		{3,5+}6,3	vxI dwdktI		{5+,3}6,3 GP5(6,3)	wyD wtkD
8	2	84	III	842	2520	1680		{3,5+}8,2	vunI dwctI		{5+,3}8,2 GP5(8,2)	wczD wcdkD
8	4	112	III	1122	3360	2240		{3,5+}8,4	vuuI dwccD		{5+,3}8,4 GP5(8,4)	wccD
11	2	147	III	1472	4410	2940		{3,5+}11,2	vvnI dwwtI		{5+,3}11,2 GP5(11,2)	wwzD
12	3	189	III	1892	5670	3780		{3,5+}12,3	vxnI dwtktktI		{5+,3}12,3 GP5(12,3)	wyzD wtktI
10	6	196	III	1962	5880	3920		{3,5+}10,6	vvuI dwwcD		{5+,3}10,6 GP5(10,6)	wwcD
12	6	252	III	2522	7560	5040		{3,5+}12,6	vxuI dwdktcI		{5+,3}12,6 GP5(12,6)	cywD wctkD
16	4	336	III	3362	10080	6720		{3,5+}16,4	vuunI dwdckD		{5+,3}16,4 GP5(16,4)	wcczD wcctI
14	7	343	III	3432	10290	6860		{3,5+}14,7	vvvI dwrwwD		{5+,3}14,7 GP5(14,7)	wwwD wrwwD
15	9	441	III	4412	13230	8820		{3,5+}15,9	vvxI dwwtkD		{5+,3}15,9 GP5(15,9)	wwxD wwtkD
16	8	448	III	4482	13440	8960		{3,5+}16,8	vuuuI dwcccD		{5+,3}16,8 GP5(16,8)	wcccD
18	1	343	III	3432	10290	6860		{3,5+}18,1	vvvI dwwwD		{5+,3}18,1 GP5(18,1)	wwwD
18	9	567	III	5672	17010	11340		{3,5+}18,9	vxxI dwtktkD		{5+,3}18,9 GP5(18,9)	wyyD wtktkD
20	12	784	III	7842	23520	15680		{3,5+}20,12	vvuuI dwwccD		{5+,3}20,12 GP5(20,12)	wwccD
20	17	1029	III	10292	30870	20580		{3,5+}20,17	vvvnI dwwwtI		{5+,3}20,17 GP5(20,17)	wwwzD wwwdkD
28	7	1029	III	10292	30870	20580		{3,5+}28,7	vvvnI dwrwwdkD		{5+,3}28,7 GP5(28,7)	wwwzD wrwwdkD

Een object met volledige icosahedrale symmetrie kan met behoud van symmetrie gewijzigd worden door op de 12 plaatsen waar de assen van orde 5 het oppervlak snijden dezelfde wijziging aan te brengen met plaatselijk behoud van de rotatie- en spiegelsymmetrie, bijvoorbeeld door een vijfhoekig zijvlak te vervangen door een samenstel van vijf driehoeken, zoals ook in een geodetische bol gebeurt, of door de ribben van het zijvlak af te knotten, of door een hoekpunt waar vijf driehoeken samenkomen af te knotten.

Uiteraard hoeft het object geen veelvlak te zijn, het oppervlak kan ook gekromd zijn. Veel variatie is ook mogelijk door beschildering, met behoud van de symmetrie. Iedere invulling is mogelijk van het fundamenteel domein, dat bestaat uit een 3D-sector tussen drie assen.