Instabilità a carico di punta
In ingegneria l'instabilità dovuta ad un carico assiale di punta agente su un'asta è un improvviso collasso di un membro strutturale soggetto ad intensi sforzi di compressione, sebbene l'effettivo sforzo di compressione generante il collasso sia minore dello sforzo massimo che il materiale componente il membro è capace di sopportare. Questo tipo di collasso è anche chiamato collasso dovuto ad instabilità elastica.
Il carico di punta assiale è una sollecitazione di compressione applicata alla testa di un'asta. Dato che nella realtà fisica è impossibile che tale compressione solleciti l'asta con uno sforzo normale puro, la sollecitazione non avrà esattamente l'asse coincidente con l'asse baricentrico della sezione, ma si troverà ad una certa distanza da esso, creando così un momento flettente.
Una struttura snella, ricevendo sollecitazioni di questo tipo, tende ad incurvarsi fino al punto di rottura ed a collassare. Perciò il fenomeno dell'instabilità a carico di punta, detta anche instabilità euleriana, instabilità a carico euleriano o, in inglese, buckling, è da evitare con grande accortezza, poiché disastroso.
Per evitare questo fenomeno, occorre prevedere correttamente i carichi di progetto e le azioni sollecitanti, modificandone eventualmente i parametri. Ad esempio:
- riducendo la compressione;
- cercando di diminuire l'eccentricità del carico;
- aumentando l'area della sezione per ridurre la flessibilità dell'asta;
- riducendo la lunghezza dell'oggetto;
- aggiungendo vincoli con altre aste vicine oppure con il suolo;
Le ultime due misure hanno lo scopo di ridurre la lunghezza di libera inflessione della trave.
Un esempio di elemento soggetto ad instabilità a carico di punta può essere un pilastro oppure una trave incastrati ad un estremo e liberi nell'altro, caratterizzati da notevole snellezza (rapporto lunghezza su diametro). Analogamente, gli alberi semi-maturi o maturi aventi un modesto valore del parametro "h/d" ("Rapporto di snellezza" o "Indice di rastremazione") sono soggetti a tale tipo di collasso. Questo tipo di sollecitazione riguarda anche le bielle dei motori veloci: quando, infatti, il pistone passa dal punto morto superiore al punto morto inferiore, e viceversa, la biella viene compressa.
Vincolamento
[modifica | modifica wikitesto]
La dimostrazione matematica di quanto segue è dovuta ad Eulero, ed è riportata più avanti.
Il profilo di inflessione dipende fortemente dalla tipologia dei vincoli. Si definisce infatti innanzitutto un coefficiente di vincolamento, indicato con μ in figura. Corrisponde al rapporto tra lunghezza di libera inflessione della trave e la sua lunghezza fisica (indicata con "l" in figura).
I valori del coefficiente per alcuni casi di vincolamento sono:
- μ = 1 per una trave vincolata con 2 cerniere agli estremi: come si vede in figura la deformata è di una semplice sinusoide che ha lunghezza d'onda uguale al doppio della lunghezza della trave
- μ = 2 per una trave vincolata con un solo incastro perfetto (mensola). Si vede in figura che la lunghezza d'onda della deformata è quattro volte la lunghezza fisica della trave
- μ = 1/2 per una trave vincolata con 2 incastri perfetti agli estremi: la lunghezza d'onda della sinusoide coincide con la lunghezza della trave
- μ = 2/3 per una trave vincolata con un incastro perfetto e una cerniera
Da questo coefficiente si calcola la lunghezza di libera inflessione una volta nota la misura della trave, con un semplice prodotto:
Snellezza
[modifica | modifica wikitesto]Viene indicato con rapporto di snellezza o semplicemente snellezza (è un numero puro):
dove:
dove:
- ρ è il raggio d'inerzia della sezione trasversale
- I è il momento d'inerzia della sezione
- A è l'area della sezione
Si calcola quindi il massimo valore di snellezza, come rapporto tra la lunghezza inflessa calcolata col coefficiente di inflessione e la misura della trave, e il valore del raggio di inerzia della trave (quello minimo se abbiamo una trave a sezione variabile). In alternativa, la formula equivalente è:
Limiti normativi
[modifica | modifica wikitesto]Per le travi in acciaio la norma italiana[1] consiglia di non superare il valore di 200 per le membrature principali e 250 per quelle secondarie.
In presenza di azioni dinamiche rilevanti, i suddetti valori devono essere limitati rispettivamente a 150 e 200.
Nelle strutture in calcestruzzo armato, vengono considerati snelli i pilastri a sezione costante per i quali la snellezza massima sia maggiore di 35.
La mancanza di una ferma prescrizione, prima presente, è dovuta al fatto che tali valori rappresentano più un limite di validità dei criteri di verifica prescritti. Al fine di dimostrare tale asserzione basta confrontare la snellezza di due profili cavi la cui sezione differisce soltanto per lo spessore. Il profilo con spessore maggiore avrà un rapporto di snellezza più elevato nonostante sia sicuramente più resistente.
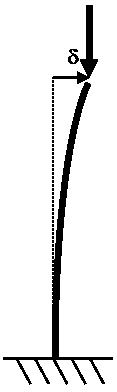
Metodo di Eulero
[modifica | modifica wikitesto]Il metodo di Eulero è un metodo ideato dallo stesso nel 1755, che prevede la risoluzione di un sistema di equazioni differenziali per la trave elastica.
La soluzione di queste equazioni fornisce la seguente espressione della tensione critica euleriana di pressoflessione[2]:
dove:
- σ è la tensione meccanica nella trave elastica lineare in esame
- E rappresenta il modulo di elasticità normale del materiale costituente la trave elastica lineare
- λ' è la snellezza (rapporto tra lunghezza inflessa (NON della trave) e raggio di inerzia.
- π è il numero pi greco
Quindi in sostanza la tensione normale di instabilità euleriana dipende solo da forma (forma della sezione e snellezza) e materiale della trave. In fase di verifica, per determinare il coefficiente di sicurezza a carico di punta questo valore va semplicemente rapportato allo sforzo normale equivalente di pressoflessione:
In fase di progetto corrispondentemente la tensione normale massima ammissibile viene determinata dal rapporto tra il carico critico euleriano e il fattore di sicurezza scelto.
Nella pratica ingegneristica tuttavia sopravvive ancora l'uso equivalente di rapportare le forze corrispondenti, nonostante l'espressione del carico critico euleriano come forza contenga più termini e quindi sia più complicata da ricordare, e dipende anche dalla grandezza della trave e non solo dalla sua forma. in altri termini travi simili e dello stesso materiale hanno la stessa tensione critica (stessi megapascal) ma diverso carico critico (diversi kilonewton).
L'espressione del carico critico euleriano in termini di forza normale è[2]:
dove i termini aggiuntivi sono:
- L0 è la lunghezza libera di inflessione
- Imin è il momento d'inerzia minimo della sezione trasversale
quindi il coefficiente di sicurezza a carico euleriano vale:
e la forza normale massima ammissibile si calcola come:
- .
Formula di Rankine
[modifica | modifica wikitesto]La formula di Rankine è tra i metodi più utilizzati per il dimensionamento a carico di punta, per la sua semplicità. Definito un carico ammissibile a compressione , calcolato dividendo il carico di snervamento del materiale per un opportuno coefficiente di sicurezza, il carico di sicurezza a carico di punta vale:
Il parametro dipende infatti dal materiale e dalla snellezza e va scelto dal progettista.
- per l'acciaio ;
- per la ghisa ;
- per il cemento armato .
Tra i valori indicati, i più bassi si applicano per basse snellezze, mentre i più alti per elevate snellezze.
Metodo Omega
[modifica | modifica wikitesto]Con il metodo delle tensioni ammissibili, per lo studio dei problemi di carico di punta è stato introdotto un metodo semplificato chiamato metodo ω.
Se consideriamo una membratura compressa assialmente, ma sufficientemente tozza in modo da poter ritenere che non possano sussistere fenomeni di instabilità (effetti del secondo ordine), il carico massimo ammissibile vale:
dove:
- σamm è la tensione ammissibile del materiale
- A è l'area della sezione trasversale della membratura.
Supponiamo di aumentare la lunghezza l del pilastro: affinché non si inneschi il fenomeno di instabilità occorre ridurre P oppure diminuire la tensione ammissibile di calcolo.
Chiamando ω il coefficiente di riduzione della σamm si avrà che il carico critico vale:
questa formula si può scrivere anche nel seguente modo:
dalla formula del carico critico di Eulero risulta che:
Pertanto:
- σcr = σamm/ω
- ω = σamm/σcr.
Si può notare che ω essendo uguale ad un rapporto di tensioni, è un numero puro che tiene conto anche della teoria di Eulero e della snellezza dell'elemento (λ).
Esistono delle apposite tabelle, per ciascun materiale, mediante le quali si determina ω in funzione del valore assunto da λ.
Con il metodo ω si può effettuare la verifica a carico di punta di un elemento snello applicando la metodologia standard per la verifiche a compressione semplice degli elementi tozzi.
Infatti determino prima la tensione agente:
Successivamente sulla base del tipo di materiale, delle caratteristiche geometriche e dei vincoli agenti determino la snellezza del pilastro e di conseguenza, dalle tabelle, il valore di ω.
A questo punto la formula di verifica a carico di punta di un elemento snello diventa la seguente:
Note
[modifica | modifica wikitesto]- ^ Gazzetta Ufficiale, su gazzettaufficiale.it. URL consultato il 13 luglio 2021.
- ^ a b Niemann, Winter, Elementi di macchine, vol.1 p.57
Bibliografia
[modifica | modifica wikitesto]Per la sezione della formula di Rankine si è fatto riferimento a: G. Cagliero, Meccanica Vol. 1, Zanichelli/E.S.A.C, Bologna 1992.
Voci correlate
[modifica | modifica wikitesto]Altri progetti
[modifica | modifica wikitesto]Wikiversità contiene risorse su Instabilità a carico di punta
Wikimedia Commons contiene immagini o altri file su Instabilità a carico di punta
| Controllo di autorità | LCCN (EN) sh85017438 · J9U (EN, HE) 987007292552405171 |
|---|