Modulo precedente Energia e lavoro

Torna a Fisica classica

Modulo successivo Dinamica dei sistemi di punti materiali

Nei sistemi di riferimento non inerziali le leggi della dinamica sono modificate e si manifestano delle forze che vengono chiamate fittizie o apparenti. Tali forze non provengono da nessuna interazione tra oggetti, ma piuttosto dalla accelerazione propria del sistema di riferimento non inerziale. Si noti che un cambiamento di sistema di riferimento ad esempio da cartesiano a polare non comporta l'insorgere di forze apparenti, anche se le leggi del moto possono variare da un tipo all'altro di sistema di riferimento.

Le forze dovute al moto relativo non uniforme tra i due sistemi di riferimento sono chiamate forze apparenti. La II legge della dinamica continua ad essere valida e quindi l'accelerazione si mantiene proporzionale alla forza.

Una forza apparente compare su un oggetto quando il sistema di riferimento usato per descrivere il movimento dell'oggetto stesso viene accelerato rispetto a un sistema di riferimento inerziale. Le accelerazioni possono avvenire in maniera molto diversa, ma per spiegare i fenomeni si enucleano 4 forze apparenti: 1) quella causata da accelerazioni in linea retta; 2) quella riguardante un sistema in rotazione (forza centrifuga); 3) moto in un sistema in rotazione (la forza di Coriolis); 4) sistema in rotazione velocità angolare variabile.

Prima di fare una analisi dettagliata si fanno degli esempi chiarificatori

Un esempio facilmente comprensibile è quello mostrato nella figura che segue nella porzione in alto. Una macchina di massa M con un passeggero di massa m in fase di accelerazione. Il passeggero si sente schiacciare contro il sedile. Nel sistema di riferimento inerziale il sedile spinge il passeggero. Mentre nel sistema di riferimento non inerziale della macchina vi è una forza fittizia -ma che spinge il passeggero contro il sedile. Vi sono quindi due modi possibili di analizzare il problema:

1. Figura centrale. Dal punto di vista di un sistema di riferimento inerziale, la macchina sta accelerando. Per mantenere il passeggero sul sedile della macchina deve essere esercitata una forza sul passeggero. La forza è la reazione vincolare del sedile, che ha incominciato a muoversi in avanti quando la macchina ha accelerato e ha compresso il sedile verso il passeggero fino a raggiungere una situazione di equilibrio dinamico in maniera che la macchina e il passeggero si muovano insieme. Il passeggero quindi viene accelerato esattamente come la macchina con la forza della spinta del sedile.
2. Figura in basso. Dal punto di vista dell'interno della macchina, un sistema di riferimento non inerziale, vi è una forza fittizia che spinge il passeggero contro il sedile, con valore pari alla massa del passeggero moltiplicata per la accelerazione della macchina. Questa forza spinge il passeggero contro il sedile, fino a quando il sedile compresso non compensa esattamente la forza fittizia. In questo sistema di riferimento il passeggero è in quiete.

Mentre nel sistema inerziale vi è solo la forza propulsiva della macchina che accelera la vettura e con essa il sedile rigidamente connesso, mentre la spinta del sedile agisce sul passeggero che si muove assieme la vettura. Nel sistema di riferimento non inerziale, la vettura in moto, lo stato di quiete è giustificato da due forze eguali ed opposte: quella fittizia del passeggero contro il sedile e quella del sedile contro il passeggero. La spiegazione fisica è più semplice nel sistema inerziale, ma la formulazione matematica potrebbe essere più complicata nel sistema inerziale. In questo caso specifico non vi è differenza di calcolo nei due sistemi di riferimento.

L'esempio illustra come le forze apparenti sono una conseguenza dell'osservazione dei fatti in un sistema di riferimento non inerziale. In alcuni casi è più semplice studiare i fenomeni dal punto di vista di un sistema non inerziale.

Un effetto simile si ha nel moto lungo un circuito circolare di una macchina. Dal punto di vista di un sistema di riferimento sulla strada si osserva un moto circolare della macchina. Quando lo stesso fenomeno è osservato in un sistema sulla macchina appare una forza apparente detta forza centrifuga. Se la macchina si muove a velocità costante lungo il tratto di strada circolare, gli occupanti della macchina si sentono spinti in fuori dal centro di rotazione dalla forza centrifuga. Anche in questo caso il fenomeno può essere visto dal punto di vista del sistema inerziale e da quello non inerziale solidale con la macchina.

1. Dal punto di vista del sistema di riferimento inerziale stazionario rispetto alla strada, la macchina ha un'accelerazione centripeta. L'accelerazione è necessaria in quanto la direzione della velocità cambia, anche se in modulo rimane costante. La accelerazione verso il centro è chiamata accelerazione centripeta e richiede una forza centripeta per permettere il moto circolare. Nel caso di una macchina, questa forza è fornita in genere dall'attrito statico tra le ruote e la strada. Questa forza causa il movimento lungo una circonferenza. In questo caso a causa dell'attrito statico tra passeggero e il sedile su cui è poggiato, anche il passeggero si muove di moto circolare uniforme come la macchina.
2. Dal punto di vista del sistema del sistema di riferimento ruotante, che si muove con la macchina, vi è una forza fittizia centrifuga che spinge gli occupanti della macchina verso l'esterno a cui ci oppone l'attrito del sedile che impedisce che le persone vadano a urtare la portiera. In questo riferimento il passeggero è fermo.

Se da una torre alta 50 m, alla latitudine dell'Italia, viene lanciato un oggetto, se l'attrito dell'aria è trascurabile esso cadrà in un punto a 7,7 mm a est dalla verticale. Dal punto di vista di un osservatore sulla Terra, sistema rotante non inerziale, vi è la forza apparente di Coriolis che causa un moto non rettilineo; dal punto di vista di un osservatore inerziale l'oggetto cade in linea retta, ma durante il tempo di caduta la Terra ruotando gli si sposta di sotto. Nei sistemi di riferimento rotanti la forza di Coriolis dipende dalla velocità relativa rispetto al sistema di riferimento non inerziale, quindi se vi è un apparente equilibrio statico non vi è nessuna forza di Coriolis. Notare che se la stessa cosa fosse stata fatta al polo non si sarebbe osservato nessun allontanamento dalla verticale, mentre se la torre si fosse trovata all'equatore si sarebbe avuta una deviazione maggiore, in quanto vi è il massimo angolo tra velocità angolare della Terra e velocità di caduta.

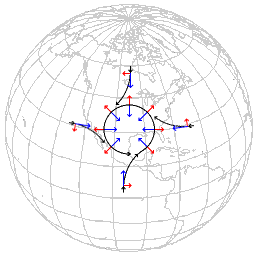
Un altro esempio di forza di Coriolis è dato da quello che succede se vi è una area di bassa pressione su cui convergono dei venti (frecce blu in figura). Se si è nell'emisfero boreale, a causa della rotazione terrestre (o, apparentemente, della forza di Coriolis) una corrente che viene da nord viene deviata verso ovest (tanto più quanto veloce è il vento), mentre una che viene da sud viene deviata verso est. Se non c'è vento, l'atmosfera ruota con la Terra e non si ha formazione di nessun vortice: è quindi la combinazione del moto della Terra e delle correnti d'aria a causare tale effetto. Come conseguenza nell'emisfero boreale i vortici girano in verso antiorario, mentre in quello australe ruotano in senso orario.

Mentre è una leggenda metropolitana il fatto che l'effetto Coriolis determini il senso di rotazione dei vortici che si creano quando si stappa lo scarico di un lavandino: nell'emisfero boreale la rotazione sarebbe in un senso (antiorario), mentre sarebbe opposta nell'emisfero australe (orario).

Se durante il moto di una macchina lungo una circonferenza varia l'intensità della velocità angolare si ha un qualcosa di simile a quello che si è descritto nel moto accelerato lineare. Dal punto di vista del sistema non inerziale vi è, oltre alla forza centrifuga, una forza apparente che spinge il passeggero verso il sedile (se la velocità angolare aumenta, se invece la macchina è in fase di decelerazione il passeggero viene spinto verso il parabrezza); quindi, l'effetto di questa forza apparente è simile a quanto avviene nel moto rettilineo. Dal punto di vista di un osservatore inerziale vi sono solo la forza centrifuga e l'accelerazione angolare con la relativa forza.

La figura a fianco è un aiuto per una formulazione analitica dei moti relativi.

Un punto materiale di massa m e posizione x_A(t) in un sistema di riferimento inerziale A. Consideriamo un sistema di riferimento non inerziale B la cui origine è nella posizione X_AB nel sistema di riferimento inerziale A. Nel sistema B la posizione del punto materiale è x_B(t). Lo scopo del ragionamento è determinare le forze apparenti agenti nel sistema di riferimento B sul punto materiale.

Gli assi delle coordinate nel riferimento B sono identificati dai versori u'_j con j = (1, 2, 3) per i tre assi delle coordinate. Quindi la posizione del punto materiale secondo il sistema B è:

${\displaystyle \mathbf {x} _{\mathrm {B} }=\sum _{j=1}^{3}x'_{j}\mathbf {u'} _{j}\ }$

Mentre nel sistema A la sua posizione è:

La derivata temporale dei versori u'_j non è nulla se il sistema B ruota. Inoltre il vettore X_AB fornisce la posizione dell'origine di B rispetto ad A, ma non include la rotazione del sistema B, in quanto la eventuale rotazione del sistema è determinata solamente dai versori.

Quindi facendo la derivata temporale della posizione istantanea (1) si ha la velocità del punto materiale:

${\displaystyle {\frac {d\mathbf {x} _{\mathrm {A} }}{dt}}={\frac {d\mathbf {X} _{\mathrm {AB} }}{dt}}+\sum _{j=1}^{3}{\frac {dx'_{j}}{dt}}\mathbf {u'} _{j}+\sum _{j=1}^{3}x'_{j}{\frac {d\mathbf {u'} _{j}}{dt}}\ .}$

Il primo termine è la velocità con cui si sposta l'origine di B (v_AB). Il secondo termine è la velocità del punto materiale, cioè v'_B nel sistema di riferimento B, quindi possiamo scrivere:

L'interpretazione di questa equazione è che la velocità del punto materiale vista dall'osservatore in A consiste di quella che l'osservatore in B chiama velocità, cioè v'_B, più due termini aggiuntivi uno dovuto alla velocità dell'origine e l'altro dovuto alla rotazione del sistema di riferimento, l'effetto di quest'ultimo termine, che si ha se il sistema non inerziale ruota, è tanto più grande quanto il punto materiale è lontano dall'origine in B .

Per ottenere l'accelerazione bisogna fare una ulteriore derivata nel tempo:

${\displaystyle {\frac {d^{2}\mathbf {x} _{\mathrm {A} }}{dt^{2}}}=\mathbf {a} _{\mathrm {AB} }+{\frac {d\mathbf {v'} _{\mathrm {B} }}{dt}}+\sum _{j=1}^{3}{\frac {dx'_{j}}{dt}}{\frac {d\mathbf {u'} _{j}}{dt}}+\sum _{j=1}^{3}x'_{j}{\frac {d^{2}\mathbf {u'} _{j}}{dt^{2}}}=\mathbf {a} _{\mathrm {AB} }+{\frac {d\mathbf {v'} _{\mathrm {B} }}{dt}}+\sum _{j=1}^{3}v'_{j}{\frac {d\mathbf {u'} _{j}}{dt}}+\sum _{j=1}^{3}x'_{j}{\frac {d^{2}\mathbf {u'} _{j}}{dt^{2}}}.}$

Usando la stessa formula già usata per la derivata temporale di x_B, le derivata della velocità (v_B) in forma esplicita diviene:

${\displaystyle {\frac {d\mathbf {v'} _{\mathrm {B} }}{dt}}=\sum _{j=1}^{3}{\frac {dv'_{j}}{dt}}\mathbf {u'} _{j}+\sum _{j=1}^{3}v'_{j}{\frac {d\mathbf {u'} _{j}}{dt}}=\mathbf {a'} _{\mathrm {B} }+\sum _{j=1}^{3}v'_{j}{\frac {d\mathbf {u'} _{j}}{dt}}}$

Di conseguenza:

Moltiplicando per la massa si ha che:

La forza osservata nel riferimento B, F_B = ma_B è dovuta alla forza reale , F_A, da:

${\displaystyle \mathbf {F'} _{\mathrm {B} }=\mathbf {F} _{\mathrm {A} }+\mathbf {F'} _{\mbox{apparenti}},}$

dove:

La prima forza apparente è dovuta all'accelerazione dell'origine di B; il secondo termine è la cosiddetta accelerazione di Coriolis (il fattore due deriva da due contributi diversi come ricavato con la derivazione analitica); il terzo termine contiene sia la accelerazione centrifuga che l'eventuale accelerazione angolare.

La seconda legge della dinamica vale anche per le forze apparenti, che possono essere considerate forze a tutti gli effetti.

Alcuni casi particolari permettono di esplicitare meglio le cose.

Se la traiettoria è rettilinea, l'espressione delle forze apparenti diventa:

Questo è il caso ad esempio di un ascensore che accelera verso l'alto con accelerazione ${\displaystyle a_{asc}\ }$; la forza che sentono i passeggeri è quindi:

${\displaystyle \mathbf {F'} _{B}=-mg-ma_{asc}}$

A cui si oppone la reazione vincolare del pavimento, ma se ponessimo una bilancia vedremmo, che mentre l'ascensore è in accelerazione in salita il peso aumenta. Nella fase di accelerazione in discesa si ha la cosa opposta, diminuisce la forza peso, al limite se la accelerazione è pari alla forza peso (l'ascensore in caduta libera) non sentiremmo nessuna forza peso. Tre esercizi chiariscono meglio quello di cui si parla: Vagone di un treno, Ascensore, Luce che cade.

Una situazione comune è quando il sistema di riferimento ruota. A causa di tale rotazione il sistema di riferimento B non è inerziale, dovuto al fatto che per avere rotazione è necessaria una accelerazione, quindi in questo caso se ci si mette nel riferimento in rotazione sono sempre presenti forze apparenti.

Per derivare l'espressione delle forze apparenti, è necessario esplicitare le derivate dei versori delle coordinate del sistema in rotazione. Se la rotazione del sistema B è rappresentata da un vettore Ω che punta lungo l'asse di rotazione con direzione determinata dalla regola della mano destra e con ampiezza data da:

${\displaystyle |{\boldsymbol {\Omega }}|={\frac {d\theta }{dt}}=\omega (t),}$

Allora la derivata prima temporale dei tre versori che descrivono il sistema B è:

${\displaystyle {\frac {d\mathbf {u'} _{j}(t)}{dt}}={\boldsymbol {\Omega }}\times \mathbf {u'} _{j}(t)}$

La derivata seconda temporale è:

${\displaystyle {\frac {d^{2}\mathbf {u'} _{j}(t)}{dt^{2}}}={\frac {d{\boldsymbol {\Omega }}}{dt}}\times \mathbf {u'} _{j}+{\boldsymbol {\Omega }}\times {\frac {d\mathbf {u'} _{j}(t)}{dt}}={\frac {d{\boldsymbol {\Omega }}}{dt}}\times \mathbf {u'} _{j}+{\boldsymbol {\Omega }}\times \left[{\boldsymbol {\Omega }}\times \mathbf {u'} _{j}(t)\right]}$

abbiamo usato le regole del prodotto vettoriale. Queste derivate sono sostituite nella espressione finale della accelerazione relativa ponendo a_AB = 0 (escludendo traslazione dell'origine e ponendo l'accento sulla sola rotazione):

${\displaystyle {\frac {d^{2}\mathbf {x} _{\mathrm {A} }}{dt^{2}}}=\mathbf {a'} _{\mathrm {B} }+2\sum _{j=1}^{3}v'_{j}\ {\frac {d\mathbf {u'} _{j}}{dt}}+\sum _{j=1}^{3}x'_{j}{\frac {d^{2}\mathbf {u'} _{j}}{dt^{2}}},}$

${\displaystyle \mathbf {a} _{\mathrm {A} }=\mathbf {a'} _{\mathrm {B} }+\ 2\sum _{j=1}^{3}v'_{j}{\boldsymbol {\Omega }}\times \mathbf {u'} _{j}(t)+\sum _{j=1}^{3}x_{j}{\frac {d{\boldsymbol {\Omega }}}{dt}}\times \mathbf {u'} _{j}\ +\sum _{j=1}^{3}x'_{j}{\boldsymbol {\Omega }}\times \left[{\boldsymbol {\Omega }}\times \mathbf {u'} _{j}(t)\right]}$

${\displaystyle =\mathbf {a'} _{\mathrm {B} }+2{\boldsymbol {\Omega }}\times \sum _{j=1}^{3}v'_{j}\mathbf {u'} _{j}(t)+{\frac {d{\boldsymbol {\Omega }}}{dt}}\times \sum _{j=1}^{3}x'_{j}\mathbf {u'} _{j}+{\boldsymbol {\Omega }}\times \left[{\boldsymbol {\Omega }}\times \sum _{j=1}^{3}x'_{j}\mathbf {u'} _{j}(t)\right].}$

Riunendo i termini, ed esprimendo in funzione di a'_B, si ha che:

L'accelerazione a_A è quella che si osserva nel sistema inerziale A ed è dovuta alle forze esterne reali, mentre l'accelerazione a'_B vista nel sistema ruotante B ha parecchi termini aggiuntivi oltre a questo

${\displaystyle -2{\boldsymbol {\Omega }}\times \mathbf {v'} _{\mathrm {B} }\ }$ è l'accelerazione di Coriolis normale alla direzione di ${\displaystyle {\boldsymbol {\Omega }}}$ (velocità angolare del sistema B) e di ${\displaystyle \mathbf {v'} _{\mathrm {B} }\ }$ (velocità del punto materiale nel sistema B). La forza di Coriolis quindi è una forza che fa deviare dalla traiettoria rettilinea che non fa lavoro e la cui azione è tanto maggiore quanto maggiore è ${\displaystyle \mathbf {v'} _{\mathrm {B} }}$.

${\displaystyle -{\frac {d{\boldsymbol {\Omega }}}{dt}}\times \mathbf {x'} _{\mathrm {B} }}$ è nella stessa direzione del moto e dipende dalla variazione nel tempo della velocità angolare del sistema di riferimento ruotante. Se la velocità angolare è costante, come nel moto dei pianeti intorno al proprio asse, tale termine è nullo.

${\displaystyle -{\boldsymbol {\Omega }}\times \left({\boldsymbol {\Omega }}\times \mathbf {x'} _{B}\right)\ }$ è la cosiddetta accelerazione centrifuga, infatti sviluppando i prodotti vettoriali, si può far vedere come sia sul piano passante per il centro di rotazione ma diretta verso l'esterno.

La forza netta sul punto materiale secondo gli osservatori sul sistema ruotante vale F'_B = ma'_B. Se le loro osservazioni sono il risultato dell'applicazione della seconda legge della dinamica, debbono considerare che la forza addizionale F'_app è presente, così che alla fine F'_B = F_A + F'_app. In poche parole, le forze apparenti dagli osservatori nel sistema B per fornire il comportamento previsto dalle leggi della dinamica è:

La terra è un sistema di riferimento ruotante con velocità angolare  ${\displaystyle {\boldsymbol {\Omega }}=7.292116\cdot 10^{-5}\ rad/s}$ che può essere considerata costante, 
essendo la sua derivata temporale solamente: 
${\displaystyle {\frac {d{\boldsymbol {\Omega }}}{dt}}=-6.47\cdot 10^{-22}\ rad/s^{2}}$
Cioè in 4 miliardi di anni il giorno è passato da circa 12 ore alle 24 ore attuali. Essendo il valore della accelerazione angolare così
piccolo, sulla terra, quindi, non vi è nessun effetto misurabile dovuto alla variazione della velocità angolare, ma invece la forza apparente
centrifuga è evidente in quanto apparentemente la forza peso è inferiore  all'equatore rispetto ai poli (l'effetto non è molto vistoso a causa
della non perfetta sfericità della terra che è schiacciata ai poli). La forza di Coriolis è molto evidente quando si hanno oggetti con 
velocità relativa molto alta rispetto alla terra in direzione non parallela all'asse di rotazione.

In questo esempio, supponiamo che il sistema di coordinate mobile B ruota su un cerchio di raggio R attorno all'origine del sistema inerziale fisso A, ma mantiene i suoi assi delle coordinate fissi in orientazione come mostrato nella figura a fianco. L'accelerazione di un punto materiale è quindi:

${\displaystyle {\frac {d^{2}\mathbf {x} _{A}}{dt^{2}}}=\mathbf {a} _{AB}+\mathbf {a'} _{B}+2\ \sum _{j=1}^{3}v'_{j}\ {\frac {d\mathbf {u'} _{j}}{dt}}}$ ${\displaystyle +\sum _{j=1}^{3}x'_{j}\ {\frac {d^{2}\mathbf {u'} _{j}}{dt^{2}}}\ .}$

${\displaystyle =\mathbf {a} _{AB}\ +\mathbf {a'} _{B}\ ,}$

Le sommatorie sono nulle in quanto i versori non hanno dipendenza dal tempo

Per esplicitare ${\displaystyle \mathbf {a} _{AB}}$, si consideri che l'origine del sistema B è posta rispetto ad A in:

${\displaystyle \mathbf {X} _{AB}=R\left(\cos(\omega t),\ \sin(\omega t)\right)\ ,}$

da questo la velocità dell'origine di B vale:

${\displaystyle \mathbf {v} _{AB}={\frac {d}{dt}}\mathbf {X} _{AB}=\mathbf {\Omega \times X} _{AB}\ ,}$

infine l'accelerazione dell'origine di B vale:

${\displaystyle \mathbf {a} _{AB}={\frac {d^{2}}{dt^{2}}}\mathbf {X} _{AB}}$ ${\displaystyle =\mathbf {\Omega \ \times } \left(\mathbf {\Omega \times X} _{AB}\right)}$ ${\displaystyle =-\omega ^{2}\mathbf {X} _{AB}\ .}$

Quindi nel sistema di riferimento B deve essere introdotta una forza apparente, che è diretta radialmente in fuori dal centro di rotazione:

${\displaystyle \mathbf {F'} _{\mathrm {app} }=m\omega ^{2}\mathbf {X} _{AB}\ ,}$

di ampiezza:

${\displaystyle |\mathbf {F'} _{\mathrm {app} }|=m\omega ^{2}R\ .}$

Nel caso del sistema ruotante la forza centrifuga dipendeva dalla distanza delle varie parti dall'origine di B, nel sistema orbitante questa forza apparente dipende dalla distanza del centro di B dal suo centro di rotazione. Quindi oggetti diversi che si trovano nel sistema orbitante B sentono la stessa forza centrifuga.

• P. Mazzoldi, M. Nigro e C. Voci, Elementi di Fisica (Meccanica e Termodinamica), 2ª ed., ISBN 978-88-7959-418-9, Edises, 2007.
• (EN) K. R. Lang Astrophysical Data: Planets and Stars, 1992, Springler-Verlag.

Argomento seguente: Dinamica dei sistemi di punti materiali