בערך זה
נעשה שימוש
בסימנים מוסכמים
מתחום המתמטיקה.
להבהרת הסימנים
ראו סימון מתמטי.
|
באלגברה ליניארית, העתקה ליניארית או טרנספורמציה ליניארית, היא העתקה (פונקציה) ממרחב וקטורי למרחב וקטורי, השומרת על החיבור והכפל בסקלר. באופן פורמלי יותר, העתקה ליניארית היא העתקה אדיטיבית והומוגנית בין שני מרחבים וקטוריים (מעל אותו שדה). מכיוון שהעתקה ליניארית שומרת על כל הפעולות, היא מהווה מורפיזם בקטגוריה של המרחבים מעל השדה.
העתקה בין מרחבים מממד סופי אפשר לתאר באמצעות מטריצה; כל מטריצה מתארת באופן חד-משמעי העתקה ליניארית, וכל העתקה ליניארית ניתנת לייצוג ככפל של מטריצה בוקטורי קואורדינטות (באופן פורמלי: מרחב ההעתקות ומרחב המטריצות איזומורפיים).
להעתקה ליניארית ממרחב  אל עצמו, כלומר
אל עצמו, כלומר  , נהוג לעיתים לקרוא אופרטור ליניארי, אך המושג אופרטור ליניארי משמש גם לתיאור העתקה ליניארית כלשהי.
, נהוג לעיתים לקרוא אופרטור ליניארי, אך המושג אופרטור ליניארי משמש גם לתיאור העתקה ליניארית כלשהי.
העתקה  ממרחב וקטורי
ממרחב וקטורי  מעל שדה F אל מרחב וקטורי
מעל שדה F אל מרחב וקטורי  מעל אותו שדה (מסמנים
מעל אותו שדה (מסמנים  ) תקרא העתקה ליניארית או טרנספורמציה ליניארית, אם מתקיימים התנאים הבאים:
) תקרא העתקה ליניארית או טרנספורמציה ליניארית, אם מתקיימים התנאים הבאים:
 משמרת חיבור (אדיטיביות): לכל שני וקטורים
משמרת חיבור (אדיטיביות): לכל שני וקטורים  השייכים למרחב
השייכים למרחב  מתקיים:
מתקיים: 
 משמרת כפל בסקלר (הומוגניות): לכל וקטור
משמרת כפל בסקלר (הומוגניות): לכל וקטור  השייך למרחב
השייך למרחב  , ולכל סקלר
, ולכל סקלר  השייך לשדה F מתקיים:
השייך לשדה F מתקיים: 
משמעות התנאים הללו היא שאין זה משנה אם מפעילים את ההעתקה  (אשר מניבה את תמונת הפונקציה) על כל וקטור בנפרד ואחר כך מחברים את התמונות, או שמחברים את הווקטורים
(אשר מניבה את תמונת הפונקציה) על כל וקטור בנפרד ואחר כך מחברים את התמונות, או שמחברים את הווקטורים  ולאחר מכן מפעילים על הסכום את העתקה – התוצאה תהיה זהה, דהיינו נשמר החיבור (אדיטיביות). באותו אופן, אין זה משנה אם מפעילים את ההעתקה
ולאחר מכן מפעילים על הסכום את העתקה – התוצאה תהיה זהה, דהיינו נשמר החיבור (אדיטיביות). באותו אופן, אין זה משנה אם מפעילים את ההעתקה  על התוצאה של כפל הווקטור
על התוצאה של כפל הווקטור  בסקלר
בסקלר  , או שמפעילים את ההעתקה על הווקטור
, או שמפעילים את ההעתקה על הווקטור  ולאחר מכן כופלים את התמונה בסקלר
ולאחר מכן כופלים את התמונה בסקלר  – הכפל נשמר (הומוגניות). שתי תכונות אלו מרכיבות את תכונת הליניאריות.
– הכפל נשמר (הומוגניות). שתי תכונות אלו מרכיבות את תכונת הליניאריות.
מההגדרה נובעת התכונה הכללית, שבהינתן וקטורים  וסקלרים
וסקלרים  מתקיים:
מתקיים:

מסקנה נוספת אשר נובעת מההגדרה, היא שהגרעין של העתקה ליניארית לעולם אינו הקבוצה הריקה ותמיד כולל את וקטור האפס  :
:

מסקנה נוספת מכך היא קריטריון הכרחי לכך שפונקציה בין מרחבים וקטוריים היא העתקה ליניארית. אם  היא העתקה ליניארית אז
היא העתקה ליניארית אז  . מאחר שקל לבדוק תנאי זה הוא מהווה כלי יעיל כדי לשלול את היותה של פונקציה חשודה העתקה ליניארית: אם T לא מעבירה אפס לאפס אז היא לא העתקה ליניארית.
. מאחר שקל לבדוק תנאי זה הוא מהווה כלי יעיל כדי לשלול את היותה של פונקציה חשודה העתקה ליניארית: אם T לא מעבירה אפס לאפס אז היא לא העתקה ליניארית.
- אם
 היא מטריצה מסדר
היא מטריצה מסדר  , אז
, אז  מגדירה העתקה ליניארית
מגדירה העתקה ליניארית  מ-
מ- ל-
ל- כאשר היא פועלת על וקטורי עמודה ב־
כאשר היא פועלת על וקטורי עמודה ב־ על ידי כפל מטריצות מימין:
על ידי כפל מטריצות מימין:  . זוהי דוגמה חשובה ושימושית ביותר, מכיוון שבדרך זו ניתן לייצג כל העתקה ליניארית בין מרחבים מממד סופי.
. זוהי דוגמה חשובה ושימושית ביותר, מכיוון שבדרך זו ניתן לייצג כל העתקה ליניארית בין מרחבים מממד סופי.
- טרנספורמציית האפס
 (פונקציה המתאימה לכל איבר בתחום את וקטור האפס בטווח) וטרנספורמציית הזהות
(פונקציה המתאימה לכל איבר בתחום את וקטור האפס בטווח) וטרנספורמציית הזהות  (פונקציה המתאימה לכל איבר בתחום את עצמו) הן טרנספורמציות ליניאריות. בפרט, אם
(פונקציה המתאימה לכל איבר בתחום את עצמו) הן טרנספורמציות ליניאריות. בפרט, אם  אז את טרנספורמציית האפס ניתן לייצג כ-
אז את טרנספורמציית האפס ניתן לייצג כ- (העתקה ליניארית באמצעות הכפלה במטריצה) כאשר
(העתקה ליניארית באמצעות הכפלה במטריצה) כאשר  היא מטריצת האפס (מטריצה בגודל המתאים שכולה אפסים), ואת טרנספורמציית הזהות
היא מטריצת האפס (מטריצה בגודל המתאים שכולה אפסים), ואת טרנספורמציית הזהות  ניתן לייצג כ-
ניתן לייצג כ- על ידי
על ידי  כאשר
כאשר  היא מטריצת היחידה מסדר
היא מטריצת היחידה מסדר  (כלומר, בגודל
(כלומר, בגודל  ).
).
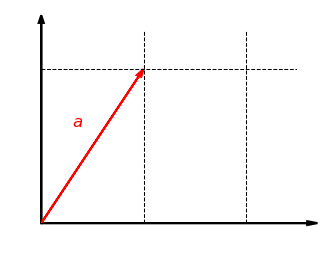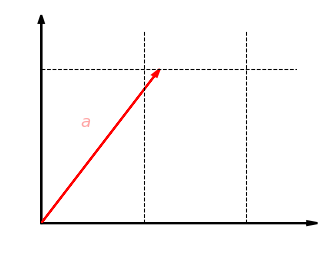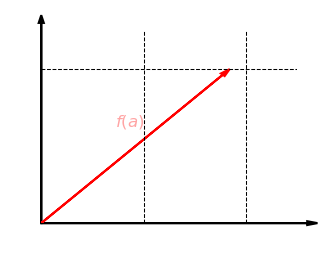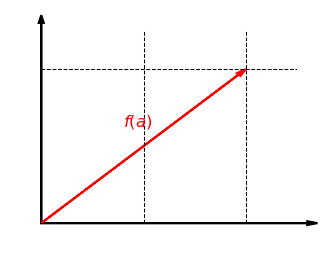
- ההעתקה
 עם
עם  היא העתקה ליניארית המותחת את ציר ה-
היא העתקה ליניארית המותחת את ציר ה- פי
פי  , בעוד את ציר ה-
, בעוד את ציר ה- היא משאירה ללא שינוי. נבטא אותה במפורש:
היא משאירה ללא שינוי. נבטא אותה במפורש:  ולכן
ולכן  . קל לבדוק ישירות שהיא אכן ליניארית. ראו המחשה גרפית שלה באיורים שבתחתית סעיף זה.
. קל לבדוק ישירות שהיא אכן ליניארית. ראו המחשה גרפית שלה באיורים שבתחתית סעיף זה.
- טרנספורמציות סיבוב ושיקוף הן טרנספורמציות ליניאריות. לדוגמה, ב-
 , הטרנספורמציה המשקפת כל וקטור יחסית לציר ה-
, הטרנספורמציה המשקפת כל וקטור יחסית לציר ה- היא טרנספורמציה ליניארית.
היא טרנספורמציה ליניארית.
- גזירה היא העתקה ליניארית ממרחב הפונקציות הגזירות למרחב הפונקציות (מרחבים מממד אינסופי).
- פונקציה
 היא העתקה ליניארית אם ורק אם היא מהצורה
היא העתקה ליניארית אם ורק אם היא מהצורה  באשר
באשר  . נשים לב שפונקציה ליניארית (כלומר: כזאת המתארת קו ישר במישור האוקלידי)
. נשים לב שפונקציה ליניארית (כלומר: כזאת המתארת קו ישר במישור האוקלידי)  היא העתקה ליניארית אם ורק אם
היא העתקה ליניארית אם ורק אם  . קל לראות שאחרת
. קל לראות שאחרת  לא מעבירה
לא מעבירה  ל-
ל- (תנאי הכרחי להעתקה ליניארית) אך ניתן להוכיח זאת גם באופן יותר מפורש: נניח ש-
(תנאי הכרחי להעתקה ליניארית) אך ניתן להוכיח זאת גם באופן יותר מפורש: נניח ש- ונראה ש-
ונראה ש- לא מקיימת אדיטיביות (ליניאריות):
לא מקיימת אדיטיביות (ליניאריות):  פונקציה
פונקציה  כזאת נקראת העתקה אפינית. נעיר שלהעתקות אפיניות יש חשיבות מיוחדת כשדנים בגזירת פונקציות בכמה משתנים (פונקציות דיפרנציאביליות).
כזאת נקראת העתקה אפינית. נעיר שלהעתקות אפיניות יש חשיבות מיוחדת כשדנים בגזירת פונקציות בכמה משתנים (פונקציות דיפרנציאביליות).
-
הפונקציה

שמוגדרת על-ידי

היא העתקה ליניארית. פונקציה זו מותחת את רכיב ה-

בפקטור

.
-
הפונקציה היא אדטיבית ושומרת על חיבור:

-
הפונקציה משמרת כפל בסקלר (
פונקציה הומוגנית): אפשר למתוח את הקלט ואז להפעיל את הפונקציה או להפעיל את הפונקציה ואז למתוח את הפלט. בניסוח מתמטי:

יהיו  ו-
ו- מרחבים וקטוריים מעל שדה כלשהו
מרחבים וקטוריים מעל שדה כלשהו  , ו-
, ו- העתקה ליניארית מ-
העתקה ליניארית מ- ל-
ל- .
.
- נאמר ש-
 היא הומומורפיזם (של מרחבים וקטוריים) אם
היא הומומורפיזם (של מרחבים וקטוריים) אם  היא העתקה ליניארית.
היא העתקה ליניארית.
- נאמר ש-
 היא מונומורפיזם אם
היא מונומורפיזם אם  חח"ע (חד חד ערכית).
חח"ע (חד חד ערכית).
- נאמר ש-
 היא אפימורפיזם אם
היא אפימורפיזם אם  על.
על.
- נאמר ש-
 היא איזומורפיזם אם
היא איזומורפיזם אם  היא הפיכה.
היא הפיכה.
מרחבים הם איזומורפיים אם קיימת ביניהם העתקה ליניארית הפיכה, ומתברר כי שני מרחבים וקטוריים איזומורפיים זה לזה אם ורק אם הם שווי-ממד. הממד מונוטוני תחת העתקות ליניאריות: אינו יורד תחת העתקה חח"ע, ואינו עולה תחת העתקה על. אם מתקיים שני מרחבים מממד סופי  ו-
ו- הם שווי ממד, אזי שלוש התכונות לעיל (חח"ע, על, הפיכות) שקולות זו לזו.
הם שווי ממד, אזי שלוש התכונות לעיל (חח"ע, על, הפיכות) שקולות זו לזו.
מכאן נובע שכל העתקה על בין מרחב ממד סופי לעצמו היא איזומורפיזם (באופן כללי אובייקט בקטגוריה שמקיים תכונה זאת נקרא הופפיאני(אנ'); כך שמרחב ממד סופי הוא הופפיאני).
באופן דומה נובע שכל העתקה חח"ע בין מרחב ממד סופי לעצמו היא איזומורפיזם (כך שמרחב ממד סופי הוא קו-הופפיאני).
אוסף כל ההעתקות הליניאריות מ- ל-
ל- מהווה בעצמו מרחב וקטורי מממד
מהווה בעצמו מרחב וקטורי מממד  . על מנת שמשפט זה יהיה מוגדר כהלכה, עלינו להגדיר חיבור של העתקות ליניאריות וכפל בסקלר. את זאת נעשה בדרך הטריוויאלית. אם
. על מנת שמשפט זה יהיה מוגדר כהלכה, עלינו להגדיר חיבור של העתקות ליניאריות וכפל בסקלר. את זאת נעשה בדרך הטריוויאלית. אם  הן העתקות ליניאריות מ-
הן העתקות ליניאריות מ- ל-
ל- , ו-
, ו- הוא אבר בשדה אז נגדיר חיבור בין העתקות וכפל של העתקה בסקלר כך:
הוא אבר בשדה אז נגדיר חיבור בין העתקות וכפל של העתקה בסקלר כך:


וקטור האפס הוא טרנספורמציית האפס.
המרחב הווקטורי של כל ההעתקות ממרחב וקטורי  למרחב וקטורי
למרחב וקטורי  מסומן
מסומן  . אם
. אם  אז
אז כלומר: מרחב הווקטורי של כל ההעתקות הליניאריות איזומורפי למרחב המטריצות עם
כלומר: מרחב הווקטורי של כל ההעתקות הליניאריות איזומורפי למרחב המטריצות עם  שורות ו-
שורות ו- עמודות.
עמודות.
תהי טרנספורמציה ליניארית  .
.
הגרעין של  , המסומן
, המסומן  (מהמילה Kernel – גרעין), הוא קבוצת הווקטורים ב-
(מהמילה Kernel – גרעין), הוא קבוצת הווקטורים ב- המועתקים על ידי
המועתקים על ידי  לווקטור האפס של
לווקטור האפס של  . כלומר:
. כלומר: .
.
משימוש בתכונות הטרנספורמציה הליניארית קל לראות כי הגרעין הוא מרחב וקטורי חלקי (תת-מרחב) ל- – משמע, הוא סגור לחיבור וכפל בסקלר. הגרעין טריוויאלי (דהיינו, שווה לתת-מרחב האפס) בדיוק כאשר
– משמע, הוא סגור לחיבור וכפל בסקלר. הגרעין טריוויאלי (דהיינו, שווה לתת-מרחב האפס) בדיוק כאשר  חח"ע.
חח"ע.
התמונה של  , המסומנת
, המסומנת  (מהמילה Image – תמונה), היא קבוצת איברי
(מהמילה Image – תמונה), היא קבוצת איברי  שקיים להם מקור ב-
שקיים להם מקור ב- , כלומר:
, כלומר:
 גם התמונה של טרנספורמציה ליניארית סגורה לחיבור וכפל בסקלר, ולכן מהווה תת-מרחב וקטורי של
גם התמונה של טרנספורמציה ליניארית סגורה לחיבור וכפל בסקלר, ולכן מהווה תת-מרחב וקטורי של  .
.
משפט הדרגה: לכל מרחב  מממד סופי ולכל טרנספורמציה ליניארית
מממד סופי ולכל טרנספורמציה ליניארית  מתקיים:
מתקיים:
 .
.
נשים לב כי בנוסחה אין תלות כלל בממד של הטווח  , אלא רק בממד של התחום
, אלא רק בממד של התחום  , הגרעין והתמונה. נובעים מן המשפט האי-שוויונות הבאים:
, הגרעין והתמונה. נובעים מן המשפט האי-שוויונות הבאים:  ולכן
ולכן 
| הוכחה
|
יהיו  בסיס של בסיס של  ויהיו ויהיו  וקטורים כך ש- וקטורים כך ש- מהווים בסיס ל- מהווים בסיס ל-
צ"ל:  מהווה בסיס ל- מהווה בסיס ל- . .
נראה כי הקבוצה בת"ל (בלתי תלויה ליניארית): יהיו  סקלרים כך ש- סקלרים כך ש-

לכן בהכרח

לכן, כיוון ש- בת"ל, לכל בת"ל, לכל  מתקיים מתקיים 
נציב ב- ונקבל כי ונקבל כי

וכיוון ש- בת"ל נקבל כי לכל בת"ל נקבל כי לכל  מתקיים כי מתקיים כי 
כלומר, רק עבור הסקלרים הטריביאליים הקומבינציה של הקבוצה  שווה שווה  ולכן הקבוצה בת”ל מעל ולכן הקבוצה בת”ל מעל  . .
נראה כי הקבוצה פורשת: יהי  , מתקיים , מתקיים  לכן, קיימים סקלרים לכן, קיימים סקלרים  כך ש- כך ש- . .
נעביר אגפים ונקבל כי
 ולכן
ולכן

לכן, קיימים סקלרים  כך ש- כך ש- ולכן ולכן

ולכן הקבוצה  פורשת את פורשת את  . .
לכן הקבוצה  מהווה בסיס עבור מהווה בסיס עבור  ולכן מתקיים ולכן מתקיים
 .
מ.ש.ל. .
מ.ש.ל.
|
יהיו  ו-
ו- מרחבים וקטורים מממד סופי מעל שדה כלשהו
מרחבים וקטורים מממד סופי מעל שדה כלשהו  , ו-
, ו- העתקה ליניארית מ-
העתקה ליניארית מ- ל-
ל- . נקבע
. נקבע  בסיס של
בסיס של  ו-
ו- בסיס של
בסיס של  . לכל וקטור ב-
. לכל וקטור ב- ניתן להתאים את וקטור הקואורדינטות שלו לפי הבסיס
ניתן להתאים את וקטור הקואורדינטות שלו לפי הבסיס  ,
, ![{\displaystyle V\ni v\mapsto [v]_{B}\in \mathbb {R} ^{n}}](https://speed.lescigales.org/xypor/index.php?q=aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy80YzdlOGE2MTJmNmU2ZWJlMGNhNGQzNzMzM2QxNDUzNTMwY2IyZDE2) ובאופן דומה
ובאופן דומה ![{\displaystyle W\ni w\mapsto [w]_{C}\in \mathbb {R} ^{m}}](https://speed.lescigales.org/xypor/index.php?q=aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy9mNTcyYzZlNWY1ZGVkZjNkNTRjMzI0N2IwZGQ4YWYyMTQxZGU3MjUz) .
.
נגדיר את המטריצה המייצגת של  ביחס לבסיסים
ביחס לבסיסים  ו-
ו- , שתסומן
, שתסומן ![{\displaystyle {[T]_{C}^{B}}\in F^{m\times n}}](https://speed.lescigales.org/xypor/index.php?q=aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy9iM2UwMjFlNTFjZjE4OTg5NjIxNWY2YmViYjljMzUyOTMyNDkwYmRi) כמטריצה שמקיימת את הקשר הבא:
כמטריצה שמקיימת את הקשר הבא:
![{\displaystyle \forall v\in V:\ \ [T(v)]_{C}=[T]_{C}^{B}[v]_{B}}](https://speed.lescigales.org/xypor/index.php?q=aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy81MDEyOTliODhkNDNhMjhkNzZmMDM3Zjc3N2E2ZmNmODY1ZGMzNWJl) ניתן לחשב אותה במפורש על ידי הנוסחה
ניתן לחשב אותה במפורש על ידי הנוסחה ![{\displaystyle \left({[T]_{C}^{B}}\right)_{ij}:=([T(v_{j})]_{C})_{i}}](https://speed.lescigales.org/xypor/index.php?q=aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy8xNDFkNzM5ZTlhZTQ0NTVkNWY4MWVjZWEzMDRmMTcwYjJjNGU1YmE0) אך בפועל ישנן דרכים פשוטות יותר לחשב אותה.
אך בפועל ישנן דרכים פשוטות יותר לחשב אותה.
- נסמן ב-
 בסיס נוסף של
בסיס נוסף של  וב-
וב- בסיס נוסף של
בסיס נוסף של  . נסמן ב-
. נסמן ב- את מטריצת המעבר מבסיס
את מטריצת המעבר מבסיס  לבסיס
לבסיס  וב-
וב- את מטריצת המעבר מבסיס
את מטריצת המעבר מבסיס  לבסיס
לבסיס  . אזי
. אזי ![{\displaystyle [T]_{C'}^{B'}=M_{C'}^{C}[T]_{C}^{B}M_{B}^{B'}}](https://speed.lescigales.org/xypor/index.php?q=aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy85YzM5NDA1MGI0NDQ3MGM0Yzc4NDEyMjc2MmNkMzhlMWY4M2JjZDAz) כאשר
כאשר  .
.
- יהי
 מרחב וקטורי נוסף מעל
מרחב וקטורי נוסף מעל  עם בסיס
עם בסיס  ותהי
ותהי  העתקה ליניארית נוספת. אזי
העתקה ליניארית נוספת. אזי ![{\displaystyle [S\circ T]_{D}^{B}=[S]_{D}^{C}[T]_{C}^{B}}](https://speed.lescigales.org/xypor/index.php?q=aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy82ZTg4OGU1YTZiYmI3ZjhhOGYzMTVkYjQ3ZTA1MDhlN2ExZmNlZTY2)
יהיו  ו-
ו- מרחבים וקטורים מעל שדה כלשהו
מרחבים וקטורים מעל שדה כלשהו  , ו-
, ו- העתקה ליניארית מ-
העתקה ליניארית מ- ל-
ל- .
.
נתבונן במרחבים הדואליים  ו-
ו- ונגדיר את ההעתקה הדואלית
ונגדיר את ההעתקה הדואלית  על ידי:
על ידי:

כאשר  ו-
ו- . עבור תת-מרחב
. עבור תת-מרחב  נסמן:
נסמן:  .
.
 היא העתקה ליניארית ומוגדרת היטב.
היא העתקה ליניארית ומוגדרת היטב. .
. .
. חח"ע אם ורק אם
חח"ע אם ורק אם  על.
על. חח"ע אם ורק אם
חח"ע אם ורק אם  על.
על.- יהי
 בסיס ל-
בסיס ל- ו-
ו- בסיס ל-
בסיס ל- . נסמן ב-
. נסמן ב- וב-
וב- בסיסים דואליים ל-
בסיסים דואליים ל- ו-
ו- בהתאמה. אזי:
בהתאמה. אזי: ![{\displaystyle {[T^{*}]_{B^{*}}^{C^{*}}}=({[T^{*}]_{C}^{B}})^{t}}](https://speed.lescigales.org/xypor/index.php?q=aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy9kYzM1NmFmNDg0MGYzN2RjNGFmOTEyZjUwMzM5ZjA0ZmYxNTk1MzY5) .
.
- נסמן ב-
 וב-
וב- את האיזומורפיזמים הקנוניים של
את האיזומורפיזמים הקנוניים של  ו-
ו- בהתאמה. נגדיר:
בהתאמה. נגדיר:  . אז מתקיים:
. אז מתקיים:  .
.

אופרטורים ליניאריים, דף שער בספרייה הלאומית