Équation de Tsiolkovski
L'équation de Tsiolkovski est l'équation fondamentale de l'astronautique, reliant l'accroissement de vitesse au cours d'une phase de propulsion d'un astronef doté d'un moteur à réaction au rapport de sa masse initiale à sa masse finale.
On la doit à Constantin Tsiolkovski et, indépendamment, à Hermann Oberth.
Histoire
[modifier | modifier le code]L'équation de Tsiolkovski[N 1] est considérée comme l'équation fondamentale de l'astronautique[1]. Son éponyme est Constantin Tsiolkovski (-), qui l'a déduite puis publiée en [4],[5],[6].
Bien que cette équation soit souvent attribuée au grand penseur autodidacte Tsiolkovski, une forme de l'équation figure déjà dans un traité du mathématicien britannique William Moore (en) (fl. c.-) paru en [7],[8],[9],[10] puis dans un article du général-major belge Casimir-Érasme Coquilhat (-) paru en [11],[12] [13],[14],[15].
L'expérience de la barque, de Tsiolkovski
[modifier | modifier le code]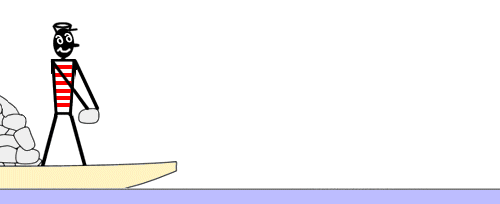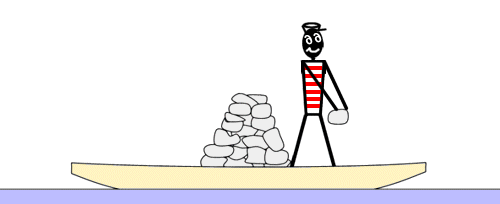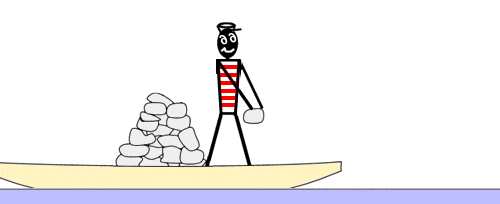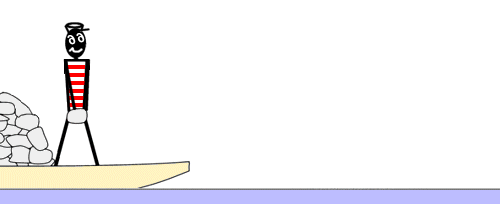
Afin de faire comprendre le principe de la propulsion à réaction, Constantin Tsiolkovski a proposé une fameuse expérience « de la barque ». Une personne se trouve démunie d'avirons dans une barque à l'écart de la rive. Elle veut rejoindre cette rive. Elle remarque que la barque est chargée d'une certaine quantité de pierres et a l'idée de lancer, une à une et le plus vivement possible, ces pierres dans la direction opposée à la rive. Effectivement, à la quantité de mouvement des pierres jetées dans un sens correspond une quantité de mouvement égale pour la barque dans l'autre sens.
Énoncé
[modifier | modifier le code]L'équation de Tsiolkovski s'écrit :
- , vectoriellement, ou , numériquement
où :
- est la variation de vitesse de l'astronef entre la fin et le début de la phase propulsée considérée ;
- est la vitesse d'éjection des gaz[N 2] ;
- est la masse totale de l'astronef au début de la phase propulsée (indice i pour initial) ;
- est la masse totale de l'astronef à l'issue de la phase propulsée (indice f pour final), exprimée dans la même unité que ;
- est la fonction logarithme népérien.
Établissement
[modifier | modifier le code]Démonstration
[modifier | modifier le code]Cette équation est établie en intégrant l'équation de conservation de la quantité de mouvement entre le début et la fin de la phase propulsée sous les hypothèses suivantes :
- l'étude du mouvement est faite dans un référentiel d'inertie ;
- l'astronef n'est soumis qu'à la force de poussée fournie par ses moteurs, aucune autre action extérieure (gravité, efforts aérodynamiques) n'est prise en compte (voir à la fin de l'article pour la prise en compte de la gravité) ;
- la vitesse d'éjection des gaz est constante.
À un instant donné, lorsque le vaisseau de masse se déplaçant à la vitesse éjecte une petite quantité d'ergol à la vitesse , on note sa variation de masse[N 3] et sa variation de vitesse. La variation de quantité de mouvement du système isolé (vaisseau + ergol éjecté) est nécessairement nulle, il vient donc :
- .
Pour obtenir la variation de vitesse de l'astronef quand sa masse passe de à , on peut intégrer cette petite variation de vitesse :
- .
Puisque , , la variation de vitesse du vaisseau a donc comme prévu la même direction que la projection des ergols et en sens opposé.
Commentaires
[modifier | modifier le code]Il est souvent dit que pour trouver cette équation, il faut que le débit massique d'ergol soit constant pendant la phase de propulsion, mais ce n'est pas obligatoire, même si cela simplifie le travail d'intégration dans un premier temps.[réf. nécessaire]
L'équation est valable aussi bien lors d'une phase d'accélération (la poussée est dans la direction de la vitesse, est positif : c'est un accroissement de vitesse) que de décélération (la poussée est de direction opposée à la vitesse, est négatif : c'est une réduction de vitesse).
La différence entre la masse initiale et la masse finale correspond à la masse que la fusée a éjectée durant sa propulsion ; on l'appelle masse d'appui[réf. nécessaire] (« d'appui » parce que c'est la masse sur laquelle la fusée s'est appuyée pour se propulser).
Pour les fusées thermo-chimiques (Ariane, Soyouz, navette, etc.), la masse d'appui est la masse des ergols (poudre, ou dioxygène et dihydrogène), laquelle est également source d'énergie chimique : c'est donc la masse d'appui elle-même qui contient l'énergie qui servira à sa propre éjection. Ce n'est plus le cas pour les moteurs ioniques (qui représentent sans doute l'avenir de la conquête spatiale). Ceux-ci sont régis tout pareillement par l'équation de Tsiolkovski, mais leur masse d'appui est constituée d'un gaz neutre (du xénon) ; c'est la très forte vitesse d'éjection de cette masse d'appui qui rend ces moteurs très économes en masse d'appui (il leur faut cependant une source d'énergie pour réaliser l'éjection). À ce titre, le fonctionnement des moteurs ioniques est comparable à celui des fusées à eau, dans lesquelles l'eau n'est utilisée que pour sa masse (l'énergie résidant dans l'air comprimé).
Dans le cas où la phase propulsée est réalisée au moyen de plusieurs étages fonctionnant successivement, la même équation de Tsiolkovski peut être utilisée pour le vol de chaque étage. On peut ainsi montrer l'intérêt de telles fusées à plusieurs étages. Voir l'exemple dans la section suivante.
Malgré l'apparente simplicité de cette équation et des hypothèses qui la sous-tendent, elle constitue une approximation utile au calcul des manœuvres de changement d'orbite, ces manœuvres étant qualifiées d'impulsionnelles, c’est-à-dire effectuées en un temps suffisamment bref pour que les hypothèses de l'équation de Tsiolkovski restent approximativement valables.
Temps nécessaire
[modifier | modifier le code]Si le vaisseau utilise un débit massique d'ergol constant on peut écrire :
- .
Or l'équation de Tsiolkovski peut s'écrire :
- .
C'est-à-dire, en changeant de signe et en passant à l'exponentielle :
- .
On en tire l'expression de qu'on reporte dans celle de :
- .
Exemple
[modifier | modifier le code]L'exemple qui suit a pour objet de montrer l'intérêt des fusées à plusieurs étages.
Soit une fusée à deux étages ayant les caractéristiques suivantes :
- la masse d'ergols embarqués par chaque étage (premier étage : 100 tonnes ; deuxième étage : 20 tonnes) représente 10 fois sa masse à vide ;
- la vitesse d'éjection des gaz est de 4 000 m/s ;
et supposons qu'elle emporte une charge utile de 2 t. Résumons ces données dans un tableau :
| Étage | Masse d'ergols (t) |
Masse à vide (t) |
Masse totale (t) |
Vitesse d'éjection des gaz (m/s) |
|---|---|---|---|---|
| Premier étage | ||||
| Deuxième étage | ||||
| Charge utile | ||||
| Total fusée |
On peut alors mener les calculs d'incréments de vitesse, comme suit, en employant deux fois l'équation de Tsiolkovski, aux étapes 3 et 6 :
| Étape de calcul | Formule | Masse (t) |
Vitesse (m/s) | |
|---|---|---|---|---|
| 1 | Masse à l'allumage du premier étage | |||
| 2 | Masse à l'extinction du premier étage | |||
| 3 | Incrément de vitesse du premier étage | |||
| 4 | Masse à l'allumage du second étage | |||
| 5 | Masse à l'extinction du second étage | |||
| 6 | Incrément de vitesse du deuxième étage | |||
| 7 | Vitesse finale | |||
Par comparaison, une fusée comportant un seul étage avec la même quantité totale d'ergols (120 t) et la même masse à vide totale (12 t) imprimerait à une charge utile de même masse (2 t) une vitesse environ 30 % inférieure :
| Étape de calcul | Formule | Masse (t) |
Vitesse (m/s) | |
|---|---|---|---|---|
| 1 | Masse à l'allumage de l'étage (unique) | |||
| 2 | Masse à l'extinction de l'étage | |||
| 3 | Vitesse finale | |||
Pertes par pesanteur
[modifier | modifier le code]Les calculs ont été effectués dans l'hypothèse d'une absence de pesanteur (manœuvres en orbite). Lorsque cette gravité agit, un terme simple doit être ajouté à l'équation de Tsiolkovski. Celle-ci devient :
- , vectoriellement, ou , si l'on projette l'équation radialement,
étant l'accélération locale de la pesanteur et la différence entre l'altitude de satellisation et celle du point de départ de la fusée. On fait l'hypothèse que est constant pendant la propulsion (alors que diminue très légèrement avec l'altitude).
Notes et références
[modifier | modifier le code]Notes
[modifier | modifier le code]- L'équation de Tsiolkovski[1] est aussi connue comme la formule de Tsiolkovski[2] ou la loi de Tsiolkovski[3].
- À partir de la vitesse d'éjection des gaz , on définit une grandeur dérivée, souvent usitée en astronautique, appelée l’impulsion spécifique du moteur, par la relation , où est l’accélération de la pesanteur (9,81 m/s2). L’impulsion spécifique a la dimension d’un temps et s’exprime donc en secondes.
- Naturellement, . La masse d'ergol éjecté est donc .
Références
[modifier | modifier le code]- Bonnal et al. 2014, § 8.2.3, p. 168, col. 1.
- Bouchez 2010, § 1.2, p. 3, col. 2.
- Rax 2005, § 1.2.3, p. 29.
- Macdonald, Norris et Spencer 2014, § 1.1.1, p. 2, col. 1.
- Macdonald, Norris et Spencer 2014, réf., p. 24, 1.
- Tsiolkovski 1903.
- Voir une mise en application de cette formule dans Journal des sciences militaires des armées de terre et de mer, tome II, 1826, [1]
- Macdonald, Norris et Spencer 2014, § 1.1.1, p. 2, col. 1-2.
- Macdonald, Norris et Spencer 2014, réf., p. 24, 2.
- Moore 1813.
- Mémoires de la Société royale des sciences de Liège, deuxième série, tome V, p. 315, [2].
- voir le lien ESA : [3]
- Macdonald, Norris et Spencer 2014, § 1.1.1, p. 2, col. 2.
- Macdonald, Norris et Spencer 2014, réf., p. 24, 3.
- Coquilhat 1873.
Voir aussi
[modifier | modifier le code]Articles connexes
[modifier | modifier le code]Publications originales
[modifier | modifier le code]- [Moore 1813] (en) Williams Moore, A treatise on the motion of rockets : to which is added an essay on navel gunnery, in theory and practice ; designed for the use of the army and navy, and in all places of military, naval and scientific instruction, Londres, .
- [Coquilhat 1873] Casimir-Érasme Coquilhat, « Trajectoires des fusées volantes dans le vide », Mémoires de la Société royale des sciences de Liège, 2e série, t. V, , art. no 5, [2]−33 p. (OCLC 248870034, lire en ligne), réimpr. :
- [Coquilhat 2018] Casimir-Érasme Coquilhat, Trajectoires des fusées volantes dans le vide : , Dijon, Nielrow, , 1re éd., 1 vol., 51 (ISBN 978-2-9559619-5-7, EAN 9782955961957, OCLC 1043726396, BNF 45456511).
- [Tsiolkovski 1903] (ru) Konstantin Èduardovič Ciolkovskij, « Исследовние мировых пространств реактивными приборами » [« L'exploration de l'espace cosmique par des engins à réaction »], Научное обозрение, vol. 7, no 5, , p. 45-75 (résumé) — publication originale de l'article de Tsiolkovski énonçant l'équation fondamentale de l'astronautique.
Bibliographie
[modifier | modifier le code] : document utilisé comme source pour la rédaction de cet article.
- [Bouchez 2010] Marc Bouchez, « Propulsion aérospatiale : lois simplifiées pour le dimensionnement et exercices d'application », Techniques de l'ingénieur, , art. BM 3 003, § 1.2 (« Formule de Tsiolkovski : cas d'une accélération constante en palier »), p. 3, col. 2 (résumé, lire en ligne).
- [Feodosiev et Siniarev 1959] (en) V. I. Feodosiev et G. B. Siniarev (trad. du russe par S. N. Samburof), Introduction to rocket technology [« Introduction à la technologie des fusées »], New York et Londres, Academic Press, (réimpr. ), 1re éd., X-344 p., in-8o (15,2 × 23,5 cm) (ISBN 978-1-4832-3201-0, EAN 9781483232010, OCLC 840470516, BNF 44667202, DOI 10.1016/C2013-0-12448-8, présentation en ligne, lire en ligne), chap. Ier (OCLC 7333041790, DOI 10.1016/B978-1-4832-3201-0.50006-1, résumé), section B (« Tsiolkovski equation for the ideal velocity of a rocket ») [« Équation de Tsiolkovski pour la vitesse idéale d'une fusée »], p. 16-22.
- [Macdonald et Badescu 2014] (en) Malcolm Macdonald et Viorel Badescu (éditeur), The international handbook of space technology [« Le guide / manuel international de la technologie spatiale »], Heidelberg et Chichester, Springer et Praxis, coll. « Praxis books / Astronautical engineering », , 1re éd., XV-731 p., 21,6 × 27,9 cm (ISBN 978-3-642-41100-7 et 978-3-662-50608-0, OCLC 958469721, BNF 44707981, DOI 10.1007/978-3-642-41101-4, SUDOC 199104573, lire en ligne) :
- [Macdonald, Norris et Spencer 2014] (en) Malcolm Macdonald, Pat Norris et David B. Spencer, « Introduction », dans op. cit., chap. 1er [« Introduction (générale) »], p. 1-24 (OCLC 7327569974, DOI 10.1007/978-3-642-41101-4_1).
- [Bonnal et al. 2014] (en) Christophe Bonnal, Alessandro Ciucci, Michael H. Obersteiner et Oskar Haidn, « Launch systems », dans op. cit., chap. 8, p. 165-195 [« Systèmes de lancement »] (OCLC 7326880462, DOI 10.1007/978-3-642-41101-4_8.
- [Macdonald, Norris et Spencer 2014] (en) Malcolm Macdonald, Pat Norris et David B. Spencer, « Introduction », dans op. cit., chap. 1er [« Introduction (générale) »], p. 1-24 (OCLC 7327569974, DOI 10.1007/978-3-642-41101-4_1).
- [Rax 2005] Jean-Marcel Rax (préf. de Bernard Bigot), Physique des plasmas : cours et applications, Paris, Dunod, coll. « Sciences sup », , 1re éd., XII-426 p., 17 × 24 cm (ISBN 978-2-10-007250-7, EAN 9782100072507, OCLC 77230441, BNF 40025642, SUDOC 090320409, présentation en ligne, lire en ligne).
- [Serra, Jung et Picard 2013] (en) Jean-Jacques Serra, Philippe Jung et Théo Pirard, « Casimir Coquilhat's theory on rocket motion : the rocket equation established in 1871 ! », dans John Harlow (éditeur), History of rocketry and astronautics (actes du 42e symposium d'histoire de l'Académie internationale d'astronautique, tenu à Glasgow en 2008), San Diego, Univelt, coll. « AAS history series » (no 39) et coll. « IAA history symposia » (no 28), , 1re éd., XII-345 p., 25 cm (ISBN 978-0-87703-589-3 et 978-0-87703-590-9, EAN 9780877035893, OCLC 840430825, présentation en ligne), 2e partie, chap. 7, p. 121-134 (résumé).
