6-hiperpluredro

6-simplaĵo (7-5-hiperĉelo) (el simplaĵa familio)	6-kruco-hiperpluredro (el kruco-hiperpluredra familio)	6-hiperkubo (el hiperkuba familio)
Latero-verticaj grafeoj de tri regulaj 5-hiperpluredroj.
6-duonvertica hiperkubo 131 (el duonvertica hiperkuba familio)	221 hiperpluredro de Gosset (duonregula)	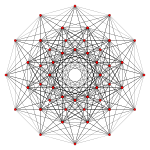122 hiperpluredro de Gosset
Latero-verticaj grafeoj de tri unuformaj 5-hiperpluredroj.

En geometrio, 6-hiperpluredro, estas 6-dimensia hiperpluredro en 6-dimensia spaco.

6-hiperpluredro estas fermita ses-dimensia figuro kun verticoj, lateroj, edroj, kaj ĉeloj, 4-hiperĉeloj kaj 5-hiperĉeloj.

• Vertico estas punkto kie 6 aŭ pli multaj lateroj kuniĝas.
• Latero estas streko kie 5 aŭ pli multaj edroj kuniĝas.
• Edro estas plurlatero kie 4 aŭ pli multaj ĉeloj kuniĝas.
• Ĉelo estas pluredro kie 3 aŭ pli multaj 4-hiperĉeloj kuniĝas. Ĉelo ludas rolon de kulmino
• 4-hiperĉelo estas plurĉelo kaj ludas rolon de kresto.
• 5-hiperĉelo estas 5-hiperpluredro kaj ludas rolon de faceto.

Plue, jenaj postuloj devas esti kontentigitaj:

• Ĉiu plurĉela 4-hiperĉelo estas komunigita per akurate du 5-hiperpluredraj facetoj.
• Najbaraj facetoj estas ne en la sama kvin-dimensia hiperebeno.
• La figuro ne estas kombinaĵo de aliaj figuroj kiuj aparte kontentigas la postulojn.

Regula 6-hiperpluredroj povas esti prezentitaj per la simbolo de Schläfli {p, q, r, s, t}, kun 5-dimensiaj facetoj {p, q, r, s} en kvanto t ĉirkaŭ ĉiu ĉelo. Estas akurate tri ĉi tiaj regulaj hiperpluredroj:

• 6-simplaĵo {3, 3, 3, 3, 3}
• 6-hiperkubo {4, 3, 3, 3, 3}
• 6-kruco-hiperpluredro {3, 3, 3, 3, 4}

Ili ĉiuj estas konveksaj. Ne ekzistas ne konveksaj regulaj 6-hiperpluredroj .

La 6-simplaĵo konsistas el 7 facetoj, ĉiu faceto estas 5-hiperĉelo. Tiel 6-simplaĵo povas esti nomata ankaŭ kiel 7-5-hiperĉelo.

Regulaj kaj uniformaj 6-hiperpluredroj kun spegula simetrio povas esti generitaj per ĉi tiuj kvar grupoj de Coxeter, prezentitaj per permutoj de ringoj de la figuroj de Coxeter-Dynkin:

#	Grupo de Coxeter		Figuro de Coxeter-Dynkin
1	A6	[35]
2	B6	[4, 34]
3	D6	[33, 1, 1]
4	E6	[33, 2, 1]

Selektitaj regulaj kaj uniformaj 6-hiperpluredroj de ĉi tiuj familioj estas:

• Simplaĵa A₆ familio: [3, 3, 3, 3, 3] -
  • 35 unuformaj 6-hiperpluredroj kiel permutoj de ringoj en la grupa figuro, inkluzivante unu regulan:
    • {3, 3, 3, 3, 3} - 6-simplaĵo aŭ 7-5-hiperĉelo,
• Hiperkuba / kruco-hiperpluredra B₆ familio: [4, 3, 3, 3, 3] -
  • 63 unuformaj tranĉoj kiel permutoj de ringoj en la grupa figuro, inkluzivanta du regulaj aĵoj:
    • {4, 3, 3, 3, 3} - 6-kubo aŭ 6-hiperkubo
    • {3, 3, 3, 3, 4} - 6-kruco-hiperpluredro
• Duonvertica hiperkuba D₆ familio: [3^{3, 1, 1}] -
  • 47 unuformaj 6-hiperpluredroj kiel permutoj de ringoj en la grupa figuro, inkluzivante:
    • {3^{1, 3, 1}} - 6-duonvertica hiperkubo , 1_{3, 1}; ankaŭ kiel h{4, 3, 3, 3, 3} .
    • {3^{3, 1, 1}} - 6-kruco-hiperpluredro , 3_{1, 1}.
• Duonregula E₆ familio: [3^{2, 2, 1}] -
  • 39 unuformaj 6-hiperpluredroj kiel permutoj de ringoj en la grupa figuro, inkluzivante:
    • {3^{2, 2, 1}} - duonregula 2₂₁ hiperpluredro de Gosset
    • {3^{1, 2, 2}} - unuforma 1₂₂ hiperpluredro de Gosset

Estas 6 unuformaj prismaj familioj bazitaj sur la uniformo 5-hiperpluredroj. Ĉiu kombinaĵo de almenaŭ unu ringo sur ĉiu koneksa grupo de figuro de Coxeter-Dynkin produktas unuforman prisman 6-hiperpluredron.

#	Grupo de Coxeter		Figuro de Coxeter-Dynkin
1	A5×A1	[3, 3, 3, 3] × [ ]
2	B5×A1	[4, 3, 3, 3] × [ ]
3	D5×A1	[32, 1, 1] × [ ]
4	A3×I2(p)×A1	[3, 3] × [p] × [ ]
5	B3×I2(p)×A1	[4, 3] × [p] × [ ]
6	H3×I2(p)×A1	[5, 3] × [p] × [ ]

Estas 11 unuformaj duprismaj familioj de hiperpluredroj bazita sur karteziaj produtoj de sube dimensiaj unuformaj hiperpluredroj. 5 estas formita kiel produtoj de unuforma plurĉelo kun regula plurlatero, kaj 6 estas formitaj kiel produtoj de du unuformaj pluredroj:

#	Grupo de Coxeter		Figuro de Coxeter-Dynkin
1	A4×I2(p)	[3, 3, 3] × [p]
2	B4×I2(p)	[4, 3, 3] × [p]
3	F4×I2(p)	[3, 4, 3] × [p]
4	H4×I2(p)	[5, 3, 3] × [p]
5	D4×I2(p)	[31, 1, 1] × [p]
6	A3×A3	[3, 3] × [3, 3]
7	A3×B3	[3, 3] × [4, 3]
8	A3×H3	[3, 3] × [5, 3]
9	B3×B3	[4, 3] × [4, 3]
10	B3×H3	[4, 3] × [5, 3]
11	H3×A3	[5, 3] × [5, 3]

Estas unu malfinia unuforma triprisma familio de hiperpluredroj konstruitaj kiel karteziaj produtoj de tri regulaj plurlateroj.

#	Grupo de Coxeter		Figuro de Coxeter-Dynkin
1	I2(p)×I2(q)×I2(r)	[p] × [q] × [r]

6-hiperpluredro povas esti konsiderata kiel kahelaro de 5-sfero (la 5-sfero estas sfero kiu estas 5-dimensia dukto, ĝi povas esti ricevita kiel rando de 6-dimensia pilko en 6-dimensia spaco; kutima sfero ekzistanta en 3-spaco estas 2-sfero). Tiel kahelaro de eŭklida 5-spaco estas simila al 6-hiperpluredro, la diferenco estas en kurbeco de la kahelata spaco.

Estas kvar fundamentaj afinaj grupoj de Coxeter kiuj generas regulajn kaj unuformajn kahelarojn en eŭklida 5-spaco:

#	Grupo de Coxeter		Figuro de Coxeter-Dynkin
1	A~5	p[36]
2	B~5	[4, 33, 4]
3	C~5	h[4, 33, 4] [4, 3, 31, 1]
4	D~5	q[4, 33, 4] [31, 1, 3, 31, 1]

Iuj regulaj kaj unuformaj kahelaroj estas:

• Regula 5-hiperkuba kahelaro, kun simboloj {4, 3³, 4}, =
• Unuforma 5-duonkuba kahelaro, kun simboloj h{4, 3³, 4}, =

• Regula hiperpluredro
• Listo de regulaj hiperpluredroj
• Unuforma hiperpluredro
• Plurlatero - 2-hiperpluredro
  • Regula plurlatero
• Pluredro - 3-hiperpluredro
  • Regula pluredro
  • Unuforma pluredro
• Plurĉelo - 4-hiperpluredro
  • Regula plurĉelo
  • Unuforma plurĉelo
• 5-hiperpluredro
• 7-hiperpluredro
• 8-hiperpluredro
• 9-hiperpluredro
• 10-hiperpluredro
• Operacioj je hiperpluredroj kaj kahelaroj:
  • Tranĉo t_{0, 1}{p, ...}
  • Laterotranĉo t_{0, 2}{p, q, ...}
  • Lateroverticotranĉo t_{0, 1, 2}{p, q, ...}
  • Edrotranĉo t_{0, 3}{p, q, r, ...}
  • Edroverticotranĉo t_{0, 1, 3}{p, q, r, ...}
  • Edrolaterotranĉo t_{0, 2, 3}{p, q, r, ...}
  • Edrolateroverticotranĉo t_{0, 1, 2, 3}{p, q, r, ...}
  • Ĉelotranĉo t_{0, 4}{p, q, r, s, ...}
  • Entutotranĉo t_{0, 1, ..., n-1}{p₁, p₂, ..., p_n-1}
  • Rektigo t₁{p, ...}
  • Dutranĉo t_{1, 2}{p, q, ...}
  • Alternado
  • Riproĉigo
• Simbolo de Schläfli - etendita simbolo de Schläfli priskribas rezultojn de la operacioj faritaj je regulaj hiperpluredroj kaj regulaj kahelaroj

• [1] Kalejdoskopoj: elektitaj skribaĵoj de H.S.M. Coxeter, 1995, ISBN 978-0-471-01003-6
• Hiperpluredraj nomoj
• Hiperpluredroj de diversaj dimensioj
• Glosaro por hiperspaco:
• Plurdimensia glosaro