In geometric graph theory, a unit disk graph is the intersection graph of a family of unit disks in the Euclidean plane. That is, it is a graph with one vertex for each disk in the family, and with an edge between two vertices whenever the corresponding vertices lie within a unit distance of each other.
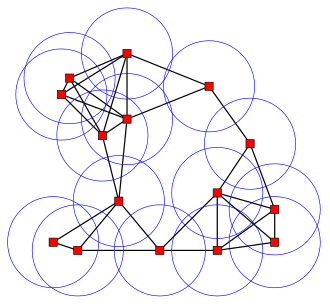
They are commonly formed from a Poisson point process, making them a simple example of a random structure.
Definitions
editThere are several possible definitions of the unit disk graph, equivalent to each other up to a choice of scale factor:
- Unit disk graphs are the graphs formed from a collection of points in the Euclidean plane, with a vertex for each point and an edge connecting each pair of points whose distance is below a fixed threshold.
- Unit disk graphs are the intersection graphs of equal-radius circles, or of equal-radius disks. These graphs have a vertex for each circle or disk, and an edge connecting each pair of circles or disks that have a nonempty intersection.
- Unit disk graphs may be formed in a different way from a collection of equal-radius circles, by connecting two circles with an edge whenever one circle contains the center of the other circle.
Properties
editEvery induced subgraph of a unit disk graph is also a unit disk graph. An example of a graph that is not a unit disk graph is the star with one central node connected to six leaves: if each of six unit disks touches a common unit disk, some two of the six disks must touch each other. Therefore, unit disk graphs cannot contain an induced subgraph.[1] Infinitely many other forbidden induced subgraphs are known.[2]
The number of unit disk graphs on labeled vertices is within an exponential factor of .[3] This rapid growth implies that unit disk graphs do not have bounded twin-width.[4]
Applications
editBeginning with the work of Huson & Sen (1995), unit disk graphs have been used in computer science to model the topology of ad hoc wireless communication networks. In this application, nodes are connected through a direct wireless connection without a base station. It is assumed that all nodes are homogeneous and equipped with omnidirectional antennas. Node locations are modelled as Euclidean points, and the area within which a signal from one node can be received by another node is modelled as a circle. If all nodes have transmitters of equal power, these circles are all equal. Random geometric graphs, formed as unit disk graphs with randomly generated disk centres, have also been used as a model of percolation and various other phenomena.[5]
Computational complexity
editIf one is given a collection of unit disks (or their centres) in a space of any fixed dimension, it is possible to construct the corresponding unit disk graph in linear time, by rounding the centres to nearby integer grid points, using a hash table to find all pairs of centres within constant distance of each other, and filtering the resulting list of pairs for the ones whose circles intersect. The ratio of the number of pairs considered by this algorithm to the number of edges in the eventual graph is a constant, giving the linear time bound. However, this constant grows exponentially as a function of the dimension.[6]
It is NP-hard (more specifically, complete for the existential theory of the reals) to determine whether a graph, given without geometry, can be represented as a unit disk graph.[7] Additionally, it is provably impossible in polynomial time to output explicit coordinates of a unit disk graph representation: there exist unit disk graphs that require exponentially many bits of precision in any such representation.[8]
However, many important and difficult graph optimization problems such as maximum independent set, graph coloring, and minimum dominating set can be approximated efficiently by using the geometric structure of these graphs,[9] and the maximum clique problem can be solved exactly for these graphs in polynomial time, given a disk representation.[10] Even if a disk representation is not known, and an abstract graph is given as input, it is possible in polynomial time to produce either a maximum clique or a proof that the graph is not a unit disk graph,[11] and to 3-approximate the optimum coloring by using a greedy coloring algorithm.[12]
See also
edit- Barrier resilience, an algorithmic problem of breaking cycles in unit disk graphs
- Indifference graph, a one-dimensional analogue of the unit disk graphs
- Penny graph, the unit disk graphs for which the disks can be tangent but not overlap (contact graph)
- Coin graph, the contact graph of (not necessarily unit-sized) disks
- Vietoris–Rips complex, a generalization of the unit disk graph that constructs higher-order topological spaces from unit distances in a metric space
- Unit distance graph, a graph formed by connecting points that are at distance exactly one rather than (as here) at most a given threshold
Notes
edit- ^ Dębski, Junosza-Szaniawski & Śleszyńska-Nowak (2020).
- ^ Atminas & Zamaraev (2018).
- ^ McDiarmid & Müller (2014).
- ^ Bonnet et al. (2022).
- ^ See, e.g., Dall & Christensen (2002).
- ^ Bentley, Stanat & Williams (1977).
- ^ Breu & Kirkpatrick (1998); Kang & Müller (2011).
- ^ McDiarmid & Mueller (2013).
- ^ Marathe et al. (1994); Matsui (2000).
- ^ Clark, Colbourn & Johnson (1990).
- ^ Raghavan & Spinrad (2003).
- ^ Gräf, Stumpf & Weißenfels (1998).
References
edit- Atminas, Aistis; Zamaraev, Viktor (2018), "On forbidden induced subgraphs for unit disk graphs", Discrete & Computational Geometry, 60 (1): 57–97, arXiv:1602.08148, doi:10.1007/s00454-018-9968-1, MR 3807349, S2CID 254025741
- Bentley, Jon L.; Stanat, Donald F.; Williams, E. Hollins Jr. (1977), "The complexity of finding fixed-radius near neighbors", Information Processing Letters, 6 (6): 209–212, doi:10.1016/0020-0190(77)90070-9, MR 0489084.
- Bonnet, Édouard; Geniet, Colin; Kim, Eun Jung; Thomassé, Stéphan; Watrigant, Rémi (2022), "Twin-width II: small classes", Combinatorial Theory, 2 (2): P10:1–P10:42, arXiv:2006.09877, doi:10.5070/C62257876, MR 4449818
- Breu, Heinz; Kirkpatrick, David G. (1998), "Unit disk graph recognition is NP-hard", Computational Geometry: Theory and Applications, 9 (1–2): 3–24, doi:10.1016/s0925-7721(97)00014-x.
- Clark, Brent N.; Colbourn, Charles J.; Johnson, David S. (1990), "Unit disk graphs", Discrete Mathematics, 86 (1–3): 165–177, doi:10.1016/0012-365X(90)90358-O.
- Dall, Jesper; Christensen, Michael (2002), "Random geometric graphs", Physical Review E, 66 (1): 016121, arXiv:cond-mat/0203026, Bibcode:2002PhRvE..66a6121D, doi:10.1103/PhysRevE.66.016121, PMID 12241440, S2CID 15193516.
- Dębski, Michał; Junosza-Szaniawski, Konstanty; Śleszyńska-Nowak, Małgorzata (2020), "Strong chromatic index of -free graphs", Discrete Applied Mathematics, 284: 53–60, doi:10.1016/j.dam.2020.03.024, MR 4115456, S2CID 216369782
- Gräf, A.; Stumpf, M.; Weißenfels, G. (1998), "On coloring unit disk graphs", Algorithmica, 20 (3): 277–293, doi:10.1007/PL00009196, MR 1489033, S2CID 36161020.
- Huson, Mark L.; Sen, Arunabha (1995), "Broadcast scheduling algorithms for radio networks", Military Communications Conference, IEEE MILCOM '95, vol. 2, pp. 647–651, doi:10.1109/MILCOM.1995.483546, ISBN 0-7803-2489-7, S2CID 62039740.
- Kang, Ross J.; Müller, Tobias (2011), "Sphere and dot product representations of graphs", Proceedings of the Twenty-Seventh Annual Symposium on Computational Geometry (SoCG'11), June 13–15, 2011, Paris, France, pp. 308–314.
- Marathe, Madhav V.; Breu, Heinz; Hunt, III, Harry B.; Ravi, S. S.; Rosenkrantz, Daniel J. (1994), Geometry based heuristics for unit disk graphs, arXiv:math.CO/9409226, Bibcode:1994math......9226M.
- Matsui, Tomomi (2000), "Approximation Algorithms for Maximum Independent Set Problems and Fractional Coloring Problems on Unit Disk Graphs", Discrete and Computational Geometry, Lecture Notes in Computer Science, vol. 1763, pp. 194–200, doi:10.1007/978-3-540-46515-7_16, ISBN 978-3-540-67181-7.
- McDiarmid, Colin; Mueller, Tobias (2013), "Integer realizations of disk and segment graphs", Journal of Combinatorial Theory, Series B, 103 (1): 114–143, arXiv:1111.2931, Bibcode:2011arXiv1111.2931M, doi:10.1016/j.jctb.2012.09.004
- McDiarmid, Colin; Müller, Tobias (2014), "The number of disk graphs", European Journal of Combinatorics, 35: 413–431, doi:10.1016/j.ejc.2013.06.037, MR 3090514
- Raghavan, Vijay; Spinrad, Jeremy (2003), "Robust algorithms for restricted domains", Journal of Algorithms, 48 (1): 160–172, doi:10.1016/S0196-6774(03)00048-8, MR 2006100, S2CID 16327087.