Bicupola
Appearance
(Redirected from Bicupola (geometry))
In geometry, a bicupola is a solid formed by connecting two cupolae on their bases. Here, two classes of bicupola are included because each cupola (bicupola half) is bordered by alternating triangles and squares. If similar faces are attached together the result is an orthobicupola; if squares are attached to triangles it is a gyrobicupola.
Forms
[edit]Set of orthobicupolae
[edit]| Symmetry | Picture | Description |
|---|---|---|
| D3h [2,3] *223 |
|
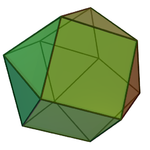
Triangular orthobicupola (J27): 8 triangles, 6 squares.[1][2] Its dual is the trapezo-rhombic dodecahedron |
| D4h [2,4] *224 |

|
Square orthobicupola (J28): 8 triangles, 10 squares.{[r|berman}} |
| D5h [2,5] *225 |

|
Pentagonal orthobicupola (J30): 10 triangles, 10 squares, 2 pentagons.{[r|berman}} |
| Dnh [2,n] *22n |
n-gonal orthobicupola: 2n triangles, 2n rectangles, 2 n-gons |
Set of gyrobicupolae
[edit]A n-gonal gyrobicupola has the same topology as a n-gonal rectified antiprism, Conway polyhedron notation, aAn.
| Symmetry | Picture | Description |
|---|---|---|
| D2d [2+,4] 2*2 |

|
Gyrobifastigium (J26) or digonal gyrobicupola: 4 triangles, 4 squares.[citation needed] |
| D3d [2+,6] 2*3 |

|
Triangular gyrobicupola or cuboctahedron: 8 triangles, 6 squares.[1][2] Its dual is the rhombic dodecahedron. |
| D4d [2+,8] 2*4 |
|
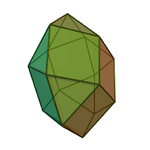
Square gyrobicupola (J29): 8 triangles, 10 squares.[2] Its dual is the elongated tetragonal trapezohedron |
| D5d [2+,10] 2*5 |
Pentagonal gyrobicupola (J31): 10 triangles, 10 squares, 2 pentagons.[2] Its dual is the elongated pentagonal trapezohedron | |
| Dnd [2+,2n] 2*n |
n-gonal gyrobicupola: 2n triangles, 2n rectangles, 2 n-gons. |
References
[edit]- ^ a b Ogievetsky, O.; Shlosman, S. (2021). "Platonic compounds and cylinders". In Novikov, S.; Krichever, I.; Ogievetsky, O.; Shlosman, S. (eds.). Integrability, Quantization, and Geometry: II. Quantum Theories and Algebraic Geometry. American Mathematical Society. p. 477. ISBN 978-1-4704-5592-7.
- ^ a b c d Berman, M. (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR 0290245.