Kurs:Mathematik (Osnabrück 2009-2011)/Teil II/Vorlesung 54/kontrolle

Zur Eindeutigkeit der Lösungen von Differentialgleichungen

Satz Satz 54.1 ändern

Es sei ${}V$ ein endlichdimensionaler reeller Vektorraum, ${}I\subseteq \mathbb {R}$ ein reelles Intervall, ${}U\subseteq V$ eine offene Menge und

f\colon I\times U\longrightarrow V,\,(t,v)\longmapsto f(t,v),

ein stetiges Vektorfeld auf ${}U$ das lokal einer Lipschitz-Bedingung genügt. Es sei ${}J\subseteq I$ ein offenes Teilintervall und es seien

v_{1},v_{2}\colon J\longrightarrow V

Lösungen des Anfangswertproblems

v'=f(t,v){\text{ und }}v(t_{0})=w.

Dann ist ${}v_{1}=v_{2}$ .

Beweis

Wir betrachten die Menge

{}M={\left\{t\in J\mid v_{1}(t)=v_{2}(t)\right\}}\,.

Wegen ${}t_{0}\in M$ ist diese Menge nicht leer. Zu jedem Punkt ${}t\in I$ gibt es nach Satz 53.4 eine offene Intervallumgebung ${}t\in J'$ , worauf es zu gegebener Anfangsbedingung ${}v(t)=v_{0}$ genau eine Lösung der Differentialgleichung gibt. Wenn ${}t\in M$ ist, so ist ${}v_{1}(t)=v_{2}(t)$ und daher stimmen ${}v_{1}$ und ${}v_{2}$ in einer offenen Umgebung ${}t\in J'$ mit der eindeutigen Lösung und damit untereinander überein. Also ist ${}J'\subseteq M$ . Dies bedeutet, dass ${}M$ eine offene Teilmenge von ${}J$ ist.
Andererseits sind ${}v_{1}$ und ${}v_{2}$ stetig und daher ist nach Aufgabe 54.1 die Menge ${}M$ auch abgeschlossen in ${}J$ .
Da ein Intervall nach Satz 21.2 zusammenhängend ist, folgt ${}M=J$ .

\Box

Das folgende Beispiel zeigt, dass ohne die Lipschitz-Bedingung die Lösung eines Anfangswertproblems nicht eindeutig bestimmt ist.

Beispiel Referenznummer erstellen

Wir betrachten das Anfangswertproblem

v'=3v^{2/3}{\text{ mit }}v(0)=0

zum zeitunabhängigen Vektorfeld

f\colon \mathbb {R} \longrightarrow \mathbb {R} ,\,v\longmapsto 3v^{2/3}=3{\sqrt[{3}]{v^{2}}}.

Offensichtlich gibt es die stationäre Lösung

{}h(t)=0\,,

aber auch

{}g(t)=t^{3}\,

ist eine Lösung, wie man durch Nachrechnen sofort bestätigt. Aus diesen beiden Lösungen kann man sich noch weitere Lösungen basteln. Es seien dazu ${}a<b$ reelle Zahlen. Dann ist auch

{}\varphi (t)={\begin{cases}(t-a)^{3}{\text{ für }}t<a,\\0{\text{ für }}a\leq t\leq b,\\(t-b)^{3}{\text{ für }}t>b,\end{cases}}\,

eine Lösung. D.h. es gibt Lösungen, bei denen das Teilchen beliebig lange (im Zeitintervall von ${}a$ nach ${}b$ ) ruht und danach (und davor) sich bewegt. Sobald sich das Teilchen in einem Punkt ${}\neq 0$ befindet, ist der Bewegungsablauf lokal eindeutig bestimmt.

Bemerkung Referenznummer erstellen

Zu einem stetigen Vektorfeld

f\colon I\times U\longrightarrow V,\,(t,v)\longmapsto f(t,v),

kann man sich fragen, ob es ein maximales Definitionsintervall ${}J$ für die Lösung eines Anfangswertproblems

v'=f(t,v){\text{ und }}v(t_{0})=w

gibt. Dies ist in der Tat der Fall, wenn das Vektorfeld lokal einer Lipschitz-Bedingung genügt! Man kann nämlich alle Teilmengen

J\subseteq I{\text{ offen }},\,t_{0}\in J,\,{\text{ es gibt eine L}}{\ddot {o}}{\text{sung }}v_{J}{\text{ auf }}J

betrachten. Wegen Satz 54.1 stimmen zwei Lösungen ${}v_{J}$ und ${}v_{J'}$ auf dem Durchschnitt ${}J\cap J'$ überein, und liefern daher eine eindeutige Lösung auf der Vereinigung ${}J\cup J'$ . Daher enthält die Menge der Teilintervalle, auf denen eine Lösung definiert ist, ein maximales Teilintervall ${}J$ .

Dieses Teilintervall kann kleiner als ${}I$ sein. Die Grenzen des maximalen Teilintervalls, auf dem eine Lösung definiert ist, heißen auch Entweichzeiten.

Gradientenfelder

Definition Referenznummer erstellen

Es sei ${}V$ ein euklidischer Vektorraum, ${}U\subseteq V$ offen und

h\colon U\longrightarrow \mathbb {R}

eine differenzierbare Funktion. Dann nennt man die Abbildung

U\longrightarrow V,\,P\longmapsto \operatorname {Grad} \,h(P),

das zugehörige Gradientenfeld.

Ein Gradientenfeld ist also ein zeitunabhängiges Vektorfeld. Man spricht auch von einem Potentialfeld, die Funktion ${}h$ (manchmal ${}-h$ ) heißt dann ein Potential des Vektorfeldes. Wenn ${}h$ zweimal stetig differenzierbar ist, so genügt nach Lemma 52.10 das zugehörige Gradientenfeld lokal einer Lipschitz-Bedingung.

Die folgende Aussage zeigt, dass die Lösungskurven der zugehörigen Differentialgleichung ${}v'=\operatorname {Grad} \,h(v)$ senkrecht auf den Fasern von ${}h$ liegen. Die Fasern beschreiben, wo das Potential (oder die Höhenfunktion) konstant ist, die Lösungen beschreiben nach Satz 46.3 den Weg des steilsten Anstiegs. Wenn ${}h$ beispielsweise die Höhenfunktion eines Gebirges ist, so gibt das Gradientenfeld in jedem Punkt den steilsten Anstieg an und die Trajektorie einer Lösungskurve beschreibt den Verlauf eines Baches (wir behaupten nicht, dass die Bewegung eines Wassermoleküls im Bach durch diese Differentialgleichung bestimmt ist, sondern lediglich, dass der zurückgelegte Weg, also das Bild der Kurve, mit dem Bild der Lösungskurve übereinstimmt). Der Bach verläuft immer senkrecht zu den Höhenlinien.

Lemma Lemma 54.5 ändern

Es sei ${}V$ ein euklidischer Vektorraum, ${}U\subseteq V$ offen,

h\colon U\longrightarrow \mathbb {R}

eine differenzierbare Funktion und

U\longrightarrow V,\,P\longmapsto G(P)=\operatorname {Grad} \,h(P),

das zugehörige Gradientenfeld. Es sei

\varphi \colon J\longrightarrow U

eine Lösung der Differentialgleichung

{}v'=G(v)\,.

Dann steht ${}\varphi '(t)$ senkrecht auf dem Tangentialraum ${}T_{\varphi (t)}F$ der Faser ${}F$ von ${}h$ durch ${}\varphi (t)$ für ${}t\in J$ , für die ${}\varphi (t)$ reguläre Punkte von ${}h$ sind.

Beweis

Sei ${}P=\varphi (t)$ ein regulärer Punkt von ${}h$ und sei ${}v\in T_{P}F=\operatorname {kern} \left(Dh\right)_{P}$ ein Vektor aus dem Tangentialraum. Dann gilt direkt

{}\left\langle v,\varphi '(t)\right\rangle =\left\langle v,G(\varphi (t))\right\rangle =\left\langle v,\operatorname {Grad} \,h(P)\right\rangle ={\left(Dh\right)}_{P}{\left(v\right)}=0\,.

\Box

Beispiel Referenznummer erstellen

Wir betrachten die Produktabbildung

h\colon \mathbb {R} ^{2}\longrightarrow \mathbb {R} ,\,(x,y)\longmapsto xy.

Das zugehörige Gradientenfeld ist

\mathbb {R} ^{2}\longrightarrow \mathbb {R} ^{2},\,(x,y)\longmapsto G(x,y)=(y,x).

Die Fasern von ${}h$ sind das Achsenkreuz (die Faser über ${}0$ ) und die durch ${}xy=c$ , ${}c\neq 0$ , gegebenen Hyperbeln. Die Lösungen der linearen Differentialgleichung

{}{\begin{pmatrix}\varphi _{1}'\\\varphi _{2}'\end{pmatrix}}={\begin{pmatrix}\varphi _{2}\\\varphi _{1}\end{pmatrix}}={\begin{pmatrix}0&1\\1&0\end{pmatrix}}{\begin{pmatrix}\varphi _{1}\\\varphi _{2}\end{pmatrix}}\,

sind von der Form

{}\varphi (t)=(\varphi _{1}(t),\varphi _{2}(t))=(a\cosh t+b\sinh t,a\sinh t+b\cosh t)\,

mit beliebigen ${}a,b\in \mathbb {R}$ , wie man direkt nachrechnet und was sich auch aus Lemma 56.1 bzw. Aufgabe ***** {{:Kurs:Kurs:Mathematik (Osnabrück 2009-2011)/Differentialgleichungssystem/(u,v)' ist (v,u)/Allgemeine Lösung/Aufgabe/Aufgabereferenznummer/Differentialgleichungssystem/(u,v)' ist (v,u)/Allgemeine Lösung/Aufgabe/Aufgabereferenznummer}} ergibt. Dabei ist ${}\varphi (0)=(a,b)$ . Für ${}a=b=0$ ist dies die stationäre Lösung im Nullpunkt, in dem die Produktabbildung nicht regulär ist. Bei ${}a=b=1$ ist ${}\varphi (t)=(e^{t},e^{t})$ , das Bild dieser Lösung ist die obere Halbdiagonale (ohne den Nullpunkt), bei ${}a=b=-1$ ist ${}\varphi (t)=(-e^{t},-e^{t})$ , das Bild dieser Lösung ist die untere Halbdiagonale, bei ${}a=1$ und ${}b=-1$ ist ${}\varphi (t)=(e^{-t},-e^{-t})$ , das Bild dieser Lösung ist die untere Hälfte der Nebendiagonalen, bei ${}a=-1$ und ${}b=1$ ist ${}\varphi (t)=(-e^{-t},e^{-t})$ , das Bild dieser Lösung ist die obere Hälfte der Nebendiagonalen.

Ansonsten treffen die Lösungskurven das Achsenkreuz in einem Punkt ${}\neq (0,0)$ . Wenn man diesen Punkt als Anfangswert zum Zeitpunkt ${}t=0$ nimmt, so kann man die Lösungskurven als

(a\cosh t,a\sinh t)

(zum Zeitpunkt $t=0$ befindet sich die Lösung auf der ${}x-$ Achse im Punkt $(a,0)$ ),

und als

(b\sinh t,b\cosh t)

(zum Zeitpunkt ${}t=0$ befindet sich die Lösung auf der ${}y-$ Achse im Punkt $(0,b)$ ) realisieren. Die Bahnen dieser Lösungen erfüllen die Gleichung ${}x^{2}(t)-y^{2}(t)=a^{2}$ bzw. ${}x^{2}(t)-y^{2}(t)=b^{2}$ , d.h. sie sind selbst Hyperbeln.

Differentialgleichungen höherer Ordnung

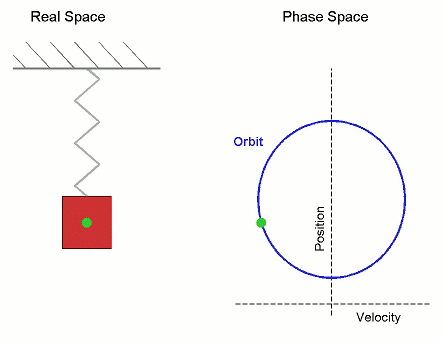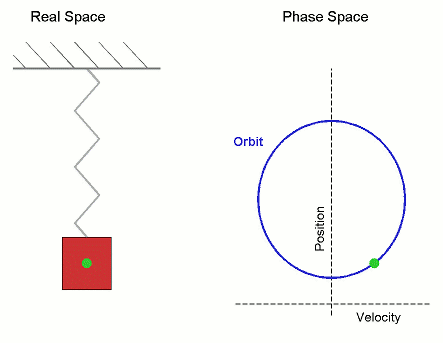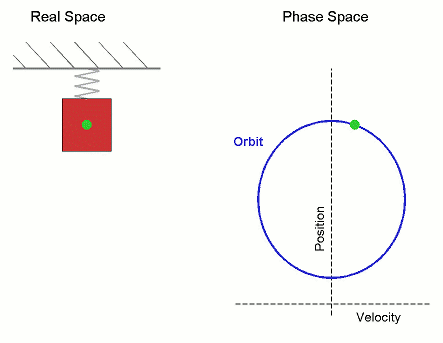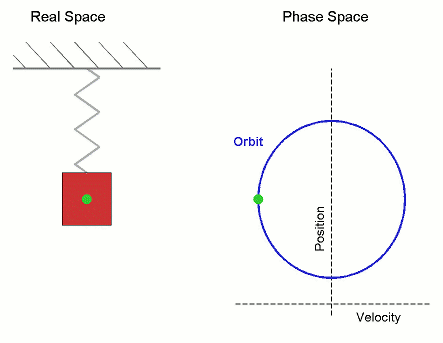
Viele physikalische Bewegungsprozesse sind nicht (wie im Fall eines Löwenzahnfallschirmchens, siehe Vorlesung 37) dadurch determiniert, dass zu jedem Zeit- und Ortspunkt die Bewegungsrichtung (also die gerichtete Geschwindigkeit) vorgegeben wird, sondern dadurch, dass zu jedem Zeit- und Ortspunkt eine Kraft auf ein Teilchen wirkt, die dieses beschleunigt. In diesem Fall kann die Bewegung also nicht durch die erste Ableitung (Geschwindigkeit) modelliert werden, sondern durch die zweite Ableitung (Beschleunigung). Typische Beispiele hierzu sind die durch Gravitation oder Federkraft hervorgerufenen Bewegungen.

Definition Referenznummer erstellen

Es sei ${}I\subseteq \mathbb {R}$ ein offenes Intervall, ${}U\subseteq \mathbb {R} ^{n}$ offen und

h\colon I\times U\longrightarrow \mathbb {R}

eine Funktion. Dann nennt man den Ausdruck

{}y^{(n)}=h{\left(t,y,y',y^{\prime \prime },\ldots ,y^{(n-1)}\right)}\,

eine Differentialgleichung der Ordnung ${}n$ .

Unter einer Lösung einer Differentialgleichung höherer Ordnung versteht man eine ${}n$ -mal differenzierbare Funktion

y\colon J\longrightarrow \mathbb {R} ,\,t\longmapsto y(t)

(wobei ${}J\subseteq I$ ein offenes Teilintervall ist) derart, dass

{}y^{(n)}(t)=h(t,y(t),y'(t),y^{\prime \prime }(t),\ldots ,y^{(n-1)}(t))\,

für alle ${}t\in J$ gilt.

Differentialgleichungen beliebiger Ordnung können unter Inkaufnahme von neuen Variablen auf ein Differentialgleichungssystem erster Ordnung zurückgeführt werden.

Lemma Lemma 54.8 ändern

Es sei ${}I\subseteq \mathbb {R}$ ein Intervall, ${}U\subseteq \mathbb {R} ^{n}$ eine offene Menge und

h\colon I\times U\longrightarrow \mathbb {R}

eine Funktion.

Dann ist die Differentialgleichung höherer Ordnung

${}y^{(n)}=h{\left(t,y,y',y^{\prime \prime },\ldots ,y^{(n-1)}\right)}\,$

über die Beziehung

${}v_{i}:=y^{(i)}\,$

äquivalent zum Differentialgleichungssystem

${}{\begin{pmatrix}v_{0}\\v_{1}\\\vdots \\v_{n-2}\\v_{n-1}\end{pmatrix}}'={\begin{pmatrix}v_{1}\\v_{2}\\\vdots \\v_{n-1}\\h(t,v_{0},v_{1},\ldots ,v_{n-1})\end{pmatrix}}\,.$

Beweis

Wenn

y\colon J\longrightarrow \mathbb {R}

eine Lösung der Differentialgleichung höherer Ordnung

{}y^{(n)}=h{\left(t,y,y',y^{\prime \prime },\ldots ,y^{(n-1)}\right)}\,

ist, so sind alle Funktionen ${}v_{i}=y^{(i)}$ für ${}i=0,\ldots ,n-1$ differenzierbar, und es gilt ${}v_{i}'=v_{i+1}$ für ${}i=0,\ldots ,n-2$ nach Definition und schließlich

{}{\begin{aligned}v_{n-1}'(t)&={\left(y^{(n-1)}\right)}^{\prime }(t)\\&=y^{(n)}(t)\\&=h{\left(t,y(t),y'(t),y^{\prime \prime }(t),\ldots ,y^{(n-1)}(t)\right)}\\&=h{\left(t,v_{0}(t),v_{1}(t),v_{2}(t),\ldots ,v_{n-1}(t)\right)}.\end{aligned}}

Wenn umgekehrt

v\colon J\longrightarrow \mathbb {R} ^{n}

eine Lösung des Differentialgleichungssystems zum Vektorfeld

F\colon I\times U\longrightarrow \mathbb {R} ^{n},\,(t,v_{0},\ldots ,v_{n-1})\longmapsto F(t,v_{0},\ldots ,v_{n-1})=(v_{1},\ldots ,v_{n-1},h(t,v_{0},v_{1},\ldots ,v_{n-1})),

ist, so ergibt sich sukzessive aus den ersten ${}n-1$ Gleichungen, dass ${}y=v_{0}$ ${}n$ -mal differenzierbar ist, und die letzte Gleichung des Differentialgleichungssystems besagt gerade

{}y^{(n)}(t)=h{\left(t,y(t),y'(t),y^{\prime \prime }(t),\ldots ,y^{(n-1)}(t)\right)}\,.

\Box

Mit dieser Umformung ist auch klar, wie sinnvolle Anfangsbedingungen für eine Differentialgleichung höherer Ordnung aussehen. Man muss nicht nur einen Startwert ${}y(t_{0})=w_{0}$ , sondern auch die höheren Ableitungen ${}y'(t_{0})=w_{1}$ , ${}y^{\prime \prime }(t_{0})=w_{2}$ , usw. festlegen.

<< | Kurs:Mathematik (Osnabrück 2009-2011)/Teil II | >>

PDF-Version dieser Vorlesung

Arbeitsblatt zur Vorlesung (PDF)