palprimes

palprimes

A prime number $p$

$p$

is a palprime if is it also palindromic, like 7, 101, or 1114111.

Clearly the property of being palindromic depends on the base. In base 10, all the palprimes except 11 have an odd number of digits, because all palindromes with an even number of digits are divisible by 11.

A few palindromic primes with palindromic index are knew. They are $p_{1}=2$ , $p_{2}=3$ , $p_{3}=5$ , $p_{4}=7$ , $p{5}=11$ , $p_{8114118}=143787341$ , and $p_{535252535}=11853735811$ .

The first palindromic primes (palprimes) are 2, 3, 5, 7, 11, 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929, 10301, 10501, 10601, 11311, 11411, 12421 more terms

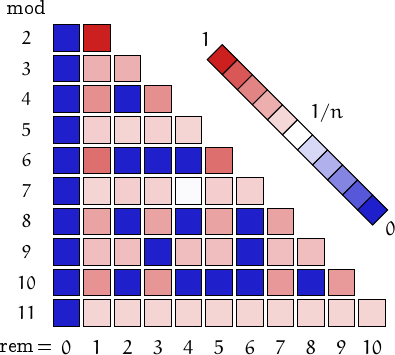
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

remainders of palprimes

Useful links Mathworld, Palindromic Prime
Wikipedia, Palindromic Prime
OEIS, Sequence A002385

Palprimes can also be... (you may click on names or numbers and on + to get more values)

a-pointer 11 101 181 30203 70207 1022201 1120211 + 967828769 aban 11 101 131 151 181 191 313 + 98600000689 alt.fact. 101 alternating 101 181 383 727 787 929 10301 + 989898989 amenable 101 181 313 353 373 757 797 + 989969989 apocalyptic 787 929 10301 10501 10601 11311 11411 + 19991 arithmetic 11 101 131 151 181 191 313 + 9989899 balanced p. 373 11411 30103 34543 35753 38183 1145411 + 996989699 c.decagonal 11 101 151 1598951 1128512158211 104216919612401 107635959536701 c.pentagonal 181 c.square 181 313 3187813 c.triangular 98689 Chen 11 101 131 181 191 353 787 + 9981899 congruent 101 151 181 191 313 353 373 + 9978799 Cunningham 101 Curzon 12821 14741 96269 1028201 1074701 1243421 1281821 + 187939781 cyclic 11 101 131 151 181 191 313 + 9989899 d-powerful 373 98389 3223223 3245423 3307033 3425243 3427243 + 9749479 de Polignac 373 757 11411 15551 16361 30403 71317 + 9965699 deficient 11 101 131 151 181 191 313 + 9989899 dig.balanced 11 787 929 10301 10601 11411 12721 + 199393991 economical 11 101 131 151 181 191 313 + 9989899 equidigital 11 101 131 151 181 191 313 + 9989899 esthetic 101 787 32323 34543 78787 1212121 3212123 + 989898787898989 Eulerian 11 evil 101 353 373 383 797 11311 12821 + 999727999 good prime 11 101 191 727 929 30803 74047 + 195353591 happy 313 383 11311 15451 30103 30803 35053 + 9935399 hex 919 Hogben 757 30103 Honaker 131 16661 33533 34543 91019 1055501 1178711 + 982323289 iban 11 101 373 727 10301 11311 11411 + 77477 inconsummate 383 16661 30703 37273 39293 70607 72727 + 73637 Jacobsthal 11 junction 101 313 919 11311 12421 12821 31513 + 9492949 Lucas 11 lucky 151 727 787 10501 13831 18181 30103 + 9514159 m-pointer 131121131 1116111116111 magnanimous 11 101 nialpdrome 11 nude 11 oban 11 313 353 373 383 727 757 + 929 odious 11 131 151 181 191 313 727 + 999565999 Ormiston 1303031 1333331 1360631 1909091 3158513 7933397 9015109 + 977999779 palindromic 11 101 131 151 181 191 313 + 999999787999999 pancake 11 191 12721 106222601 panconsummate 11 353 pandigital 11 partition 11 101 pernicious 11 131 151 181 191 313 727 + 9981899 plaindrome 11 prime 11 101 131 151 181 191 313 + 99999199999 Proth 353 929 96769 repdigit 11 repunit 757 30103 self 727 929 30403 34543 35353 78887 79697 + 998282899 sliding 11 101 Sophie Germain 11 131 191 12821 14741 19391 19991 + 999212999 star 181 12421 18481 121959676959121 314435969534413 396868131868693 strobogrammatic 11 101 181 18181 1008001 1180811 1880881 + 188888888888881 strong prime 11 101 191 727 757 787 929 + 9980899 super-d 131 181 919 10301 10501 10601 13331 + 9907099 truncatable prime 313 353 373 383 797 76367 79397 + 799636997 twin 11 101 151 181 191 313 10301 + 999454999 uban 11 19000000091 32000000023 35000000053 37000000073 98000000089 1000008000001 + 9000007000009 Ulam 11 131 10501 13931 30703 30803 32423 + 9871789 undulating 101 131 151 181 191 313 353 + 737373737373737 weak prime 131 151 181 313 353 383 797 + 9989899 weakly prime 79856965897 91507670519 Woodall 191 383 Zuckerman 11 zygodrome 11 1177711 7722277 7733377 331111133 772222277 779999977 + 999955444559999