The Eulerian number  , often denoted with
, often denoted with 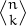 is the number of permutations of the numbers
is the number of permutations of the numbers 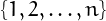 in which
in which 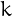 elements are greater than the previous element, i.e., the number of permutations with
elements are greater than the previous element, i.e., the number of permutations with 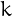 ascents.
ascents.
![\[
\Eul{n}{k}=\sum_{i=0}^{k+1}(-1)^i(k-i+1)^n{{n+1}\choose i}\,,
\]](https://speed.lescigales.org/xypor/index.php?q=aHR0cHM6Ly93d3cubnVtYmVyc2FwbGVudHkuY29tL3NldC9FdWxlcmlhbl9udW1iZXIvcGljLjEwLnBuZw%3D%3D) and are involved in many indentities, like
and are involved in many indentities, like
![\[
n!=\sum_{k=0}^{n}\Eul{n}{k}\quad\mathrm{and}\quad x^n = \sum_{k=0}^{n-1}\Eul{n}{k}{{x+k}\choose n}\,.
\]](https://speed.lescigales.org/xypor/index.php?q=aHR0cHM6Ly93d3cubnVtYmVyc2FwbGVudHkuY29tL3NldC9FdWxlcmlhbl9udW1iZXIvcGljLjExLnBuZw%3D%3D)
For example, among the permutations of
, there are
permutations with 2 ascents, like
, and
.
Eulerian numbers are given by the formula
The first distinct Eulerian numbers are 1, 4, 11, 26, 57, 66, 120, 247, 302, 502, 1013, 1191, 2036, 2416, 4083, 4293, 8178, 14608, 15619, 16369, 32752, 47840, 65519, 88234, 131054, 152637, 156190 more terms
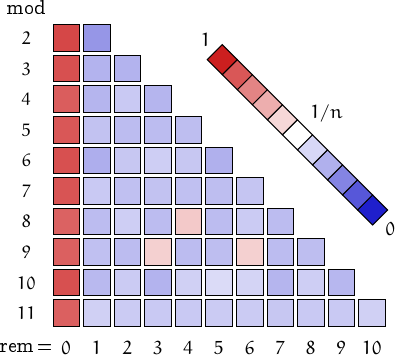
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
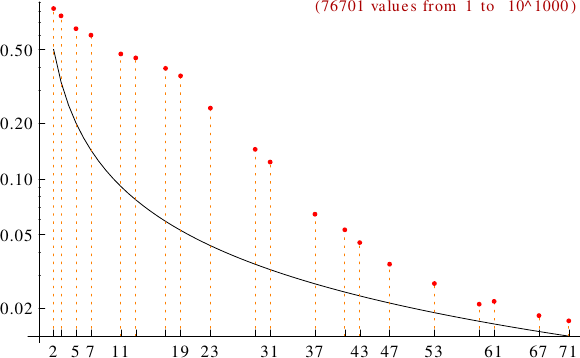
A graph displaying how many Eulerian numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.
Eulerian numbers can also be... (you may click on names or numbers and on + to get more values)
a-pointer
11
aban
11
26
57
66
120
247
302
502
abundant
66
120
8178
14608
32752
47840
131054
524268
1479726
+
33554406
admirable
66
120
alternating
16369
amenable
57
120
1013
2036
2416
4293
14608
16369
32752
+
848090912
apocalyptic
247
1191
4083
8178
14608
15619
16369
arithmetic
11
57
66
247
302
502
1013
1191
2036
+
9738114
binomial
66
120
brilliant
247
c.decagonal
11
c.square
1013
cake
26
Chen
11
65519
478271
congruent
120
247
302
502
1013
1191
2036
2416
4293
+
2203488
constructible
120
Cunningham
26
120
Curzon
26
1013
131054
45533450
198410786
cyclic
11
247
1013
4083
15619
16369
65519
478271
1048555
4194281
D-number
57
1191
4083
de Polignac
65519
deficient
11
26
57
247
302
502
1013
1191
2036
+
8388584
dig.balanced
11
120
302
502
15619
47840
152637
4537314
10187685
134217700
Duffinian
57
247
1191
1048555
eban
66
2036
economical
11
1013
1191
4293
15619
16369
65519
152637
478271
+
13824739
emirpimes
26
302
502
equidigital
11
1013
1191
4293
15619
16369
65519
152637
478271
+
13824739
evil
57
66
120
1013
1191
2036
4083
8178
47840
+
423281535
factorial
120
Friedman
524268
gapful
120
47840
131054
156190
262125
2203488
10187685
126781020
134217700
+
14875399450
good prime
11
65519
happy
302
2036
32752
1479726
Harshad
120
247
47840
131054
134217700
3464764515
hexagonal
66
120
highly composite
120
hoax
152637
Hogben
57
1191
Honaker
67108837
iban
11
120
247
302
idoneal
57
120
inconsummate
4293
262125
interprime
26
120
4293
47840
8388584
10187685
16777191
Jacobsthal
11
Jordan-Polya
120
junction
1013
2416
88234
262125
13824739
Lehmer
247
Leyland
57
lonely
120
Lucas
11
lucky
152637
magnanimous
11
metadrome
26
57
247
modest
26
2036
Moran
247
nialpdrome
11
66
nude
11
66
oban
11
26
57
66
odious
11
26
247
302
502
2416
4293
14608
15619
+
848090912
palindromic
11
66
palprime
11
pancake
11
2416
panconsummate
11
57
pandigital
11
120
partition
11
pentagonal
247
pernicious
11
26
66
247
302
502
2416
4293
14608
+
8388584
plaindrome
11
26
57
66
247
practical
66
120
14608
32752
47840
2203488
prim.abundant
66
131054
prime
11
1013
15619
16369
65519
478271
13824739
67108837
primeval
1013
Proth
57
pseudoperfect
66
120
8178
14608
32752
47840
131054
524268
repdigit
11
66
repunit
57
1191
self
15619
67108837
848090912
semiprime
26
57
247
302
502
1191
4083
41932745
sliding
11
502
Smith
152637
Sophie Germain
11
1013
sphenic
66
88234
152637
156190
1048555
1310354
4194281
16777191
strobogrammatic
11
strong prime
11
15619
65519
478271
13824739
super Niven
120
super-d
247
15619
16369
65519
156190
2203488
4194281
superabundant
120
tau
524268
2203488
8388584
tetrahedral
120
triangular
66
120
twin
11
65519
478271
uban
11
26
57
66
Ulam
11
26
57
502
1191
2097130
unprimeable
14608
32752
156190
455192
untouchable
120
2036
2416
455192
524268
wasteful
26
57
66
120
247
302
502
2036
2416
+
9738114
weak prime
1013
16369
67108837
Zuckerman
11
Zumkeller
66
120
8178
14608
32752
47840
zygodrome
11
66