So called by Richard Duffy who introduced them, they are those composite
numbers 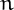 which have no prime factors in common with the sum of
their divisors
which have no prime factors in common with the sum of
their divisors 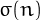 .
.
For example, 35 is Duffinian since it is relatively prime to the sum of its divisors 1 + 5 + 7 + 35 = 48.
It is easy to see that there are
infinite such numbers. Indeed any number of the form where
is prime
and
is Duffinian, since
cannot be
divisible by
.
P. Heichelheim proved that exists a run of 5 consecutive Duffinian numbers starting at 202605639573839041, and that cannot exist a longer such run.
Rose Mary Zbiek has proved that every even Duffinian number is either a square or twice a square.
The smallest 3 × 3 magic square whose entries are consecutive Duffinian numbers is
| 18649 | 18631 | 18643 |
| 18635 | 18641 | 18647 |
| 18639 | 18651 | 18633 |
The first Duffinian numbers are 4, 8, 9, 16, 21, 25, 27, 32, 35, 36, 39, 49, 50, 55, 57, 63, 64, 65, 75, 77, 81, 85, 93, 98, 100 more terms
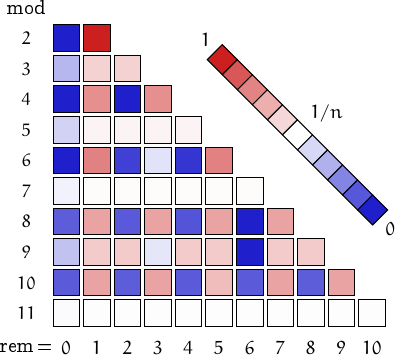
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
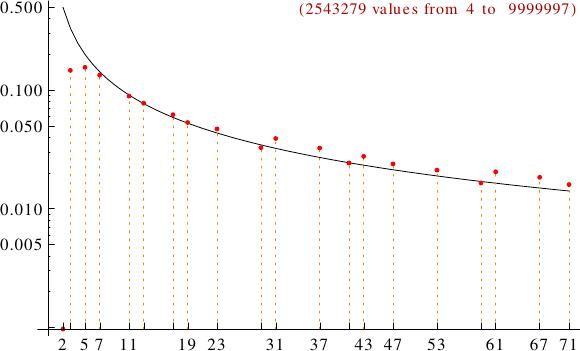
A graph displaying how many Duffinian numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.
Useful links
OEIS, Sequence A003624
Duffinian numbers can also be... (you may click on names or numbers and on + to get more values)
ABA
32
50
64
+
9999392
aban
16
21
25
+
9000999
abundant
36
100
144
+
9999392
Achilles
392
800
968
+
9999392
alt.fact.
326981
alternating
16
21
25
+
9898987
amenable
16
21
25
+
9999997
apocalyptic
243
245
247
+
29999
arithmetic
21
27
35
+
9999997
astonishing
27
3591
23287
+
2732353
automorphic
25
625
2890625
Bell
203
4213597
betrothed
75
1575
1925
+
2576945
binomial
21
35
36
+
9956953
brilliant
21
25
35
+
9999811
c.decagonal
361
451
551
+
9989911
c.heptagonal
253
841
1331
+
9966797
c.nonagonal
55
253
325
+
9956953
c.octagonal
25
49
81
+
9991921
c.pentagonal
16
391
1156
+
9955051
c.square
25
85
221
+
9994921
c.triangular
64
85
235
+
9988471
cake
64
93
299
+
9735503
Canada
125
8549
16999
Carmichael
1105
8911
15841
+
9613297
Carol
959
65023
261119
4190207
congruent
21
39
55
+
9999997
constructible
16
32
64
+
8388608
cube
27
64
125
+
9393931
Cullen
25
65
161
+
4718593
Cunningham
35
50
63
+
9998243
Curzon
21
50
65
+
9999921
cyclic
35
65
77
+
9999997
D-number
21
39
57
+
7043133
d-powerful
63
175
209
+
9999865
de Polignac
905
959
1207
+
9999997
decagonal
27
85
175
+
9968227
deceptive
259
451
481
+
9897121
deficient
16
21
25
+
9999997
dig.balanced
21
35
49
+
9999993
droll
800
5184
6272
+
5017600
eban
32
36
50
+
4032064
economical
16
21
25
+
9999803
emirpimes
39
49
85
+
9999967
enlightened
256
2048
2304
+
3720087
equidigital
16
21
25
+
9999625
eRAP
98
2255
7625
+
9960047
esthetic
21
32
65
+
9898987
Eulerian
57
247
1191
1048555
evil
27
36
39
+
9999993
fibodiv
75
183
305
+
8899945
Fibonacci
21
55
144
+
9227465
Friedman
25
121
125
+
999163
frugal
125
128
243
+
9999803
gapful
100
121
143
+
9999827
Gilda
49
977909
3242189
+
4848955
happy
32
49
100
+
9999983
Harshad
21
27
36
+
9999881
heptagonal
55
81
189
+
9967027
hex
169
217
469
+
9986401
hexagonal
325
1225
3655
+
9916831
highly composite
36
hoax
85
265
319
+
9999355
Hogben
21
57
111
+
9988761
house
32
155
1285
+
9716393
hungry
144
161449
712201
2401519
hyperperfect
21
301
325
+
9699181
iban
21
27
77
+
777773
iccanobiF
39
1053
12815
+
792517
idoneal
16
21
25
+
385
impolite
16
32
64
+
8388608
inconsummate
63
65
75
+
999993
insolite
111
interprime
21
39
50
+
9999755
Jacobsthal
21
85
171
+
1398101
Jordan-Polya
16
32
36
+
9437184
junction
111
115
305
+
9999959
Kaprekar
55
999
7777
+
5072059
katadrome
21
32
50
+
9876541
Kynea
4223
16639
1050623
4198399
Lehmer
85
133
247
+
9996205
Leyland
32
57
100
+
8389137
lonely
1343
31429
31431
+
4652429
Lucas
15127
39603
64079
+
4870847
lucky
21
25
49
+
9999997
Lynch-Bell
36
128
175
+
1382976
magic
65
111
175
+
9951391
magnanimous
16
21
25
+
8844449
metadrome
16
25
27
+
2456789
modest
39
49
111
+
9998991
Moran
21
27
63
+
9999881
Motzkin
21
323
835
narcissistic
371
407
92727
1741725
nialpdrome
21
32
50
+
9999997
nonagonal
75
111
325
+
9885961
nude
36
55
77
+
9977373
O'Halloran
36
oban
16
25
27
+
999
octagonal
21
65
133
+
9988225
odious
16
21
25
+
9999997
palindromic
55
77
111
+
9998999
pancake
16
121
301
+
9997157
panconsummate
21
36
39
+
3097
pandigital
21
75
201
+
9998163
partition
77
385
1255
+
9289091
pentagonal
35
247
425
+
9991051
pernicious
21
25
35
+
9999997
Perrin
39
119
209
+
2240877
plaindrome
16
25
27
+
8999999
Poulet
341
1105
1387
+
9995671
power
16
25
27
+
9991921
powerful
16
25
27
+
9999392
practical
16
32
36
+
9999392
prim.abundant
1575
1660725
2553525
+
9819225
primeval
1037
1079
1379
+
1234679
pronic
2450
2827442
Proth
25
49
57
+
9998337
pseudoperfect
36
100
144
+
1000000
rare
65
repdigit
55
77
111
+
7777777
repfigit
75
1537
7385
+
7913837
repunit
21
57
63
+
9988761
Rhonda
12985
15625
19435
+
8519579
Ruth-Aaron
16
25
49
+
9997417
Saint-Exupery
202500
Sastry
183
715
self
64
75
121
+
9999965
semiprime
21
25
35
+
9999997
sliding
25
65
133
+
9868025
Smith
27
85
121
+
9999355
sphenic
385
399
595
+
9999983
square
16
25
36
+
9991921
star
121
253
793
+
9992341
straight-line
111
333
543
+
7777777
strobogrammatic
111
689
1111
+
6998669
subfactorial
265
super Niven
36
50
100
+
9000000
super-d
81
119
169
+
9999919
superabundant
36
tau
36
128
225
+
9903609
taxicab
20683
195841
327763
+
9443761
tetrahedral
35
1771
6545
+
9290431
tetranacci
20569
283953
547337
triangular
21
36
55
+
9956953
tribonacci
81
927
1705
+
1389537
trimorphic
25
49
75
+
7890625
uban
16
21
25
+
9000099
Ulam
16
36
57
+
9999977
undulating
121
161
171
+
9797979
unprimeable
324
325
512
+
9999965
untouchable
324
576
784
+
984064
upside-down
55
64
1379
+
9995111
vampire
2187
117067
124483
+
536539
wasteful
36
39
50
+
9999997
Wieferich
3279
7651
10533
+
3837523
Woodall
63
323
2047
+
9961471
Zeisel
4505
5719
24211
+
9773731
Zuckerman
36
111
115
+
7111111
Zumkeller
1575
14175
39375
+
96075
zygodrome
55
77
111
+
9999977