Canada numbers are those 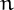 such that the sum of the squares of the digits
of
such that the sum of the squares of the digits
of 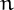 is equal to the sum of the non-trivial divisors of
is equal to the sum of the non-trivial divisors of 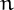 , i.e.
, i.e.  .
.
For example, 581, whose divisors are 1, 7, 83 and 581,
is a Canada number because .
The name of these numbers is due to the fact they were defined by some mathematicians from Manitoba University to celebrate the 125th anniversary of Canada.
The Canada numbers are 125, 581, 8549, and 16999.
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

Useful links
OEIS, Sequence A070308
Canada numbers can also be... (you may click on names or numbers)
aban
125
581
alternating
125
581
8549
amenable
125
581
8549
apocalyptic
8549
16999
arithmetic
125
581
8549
16999
congruent
125
581
8549
16999
cube
125
Curzon
125
581
8549
cyclic
581
8549
16999
deficient
125
581
8549
16999
Duffinian
125
8549
16999
economical
125
581
16999
emirpimes
581
8549
equidigital
581
16999
evil
125
581
8549
Friedman
125
frugal
125
happy
16999
inconsummate
8549
metadrome
125
modest
16999
odious
16999
pernicious
16999
plaindrome
125
16999
power
125
powerful
125
Ruth-Aaron
125
semiprime
581
8549
16999
super-d
581
trimorphic
125
wasteful
8549