[go: up one dir, main page]
Search a number
Bell numbers
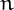The  $n$-th Bell number  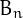$B_n$  is equal to the number of ways in which 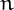 $n$  objects can be partitioned into non-empty subsets.

For example,  $B_3 = 5$  because the set  $\{a, b, c\}$  can be partitioned in 5 ways:  $\{\{a\}, \{b\}, \{c\}\}$,  $\{\{a\}, \{b, c\}\}$,  $\{\{b\}, \{a, c\}\}$,  $\{\{c\}, \{a, b\}\}$  and  $\{\{a, b, c\}\}.$

Two classical formulas

\[ B_{n+1}=\sum_{k=0}^n{n\choose k}B_k\,,\quad\quad% B_n = \left\lceil\frac{1}{e}\sum_{k=1}^{2n}\frac{k^n}{k!}\right\rceil\,.\]

The first Bell numbers are 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975, 678570, 4213597, 27644437, 190899322, 1382958545, 10480142147, 82864869804, 682076806159, 5832742205057, 51724158235372, 474869816156751.

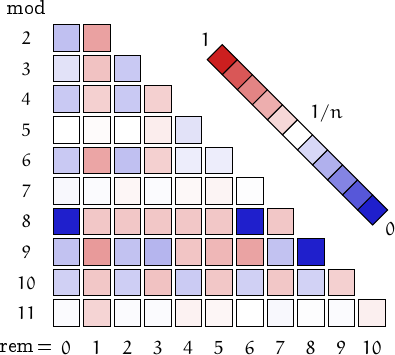
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
remainders of Bell numbers

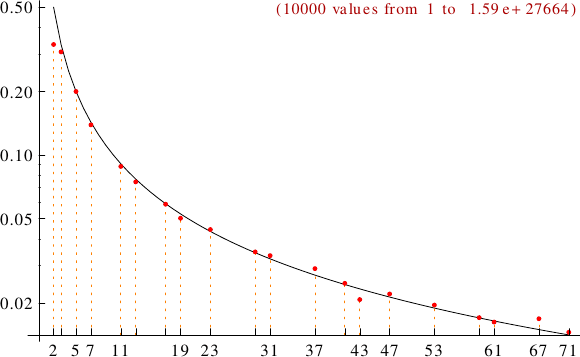
A graph displaying how many Bell numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.
divisibility of Bell numbers
Useful links Mathworld, Bell Number
Wikipedia, Bell number
OEIS, Sequence A000110
Bell numbers can also be... (you may click on names or numbers)

aban 15 52 203 877 abundant 4140 678570 alternating 52 amenable 52 877 4140 4213597 27644437 apocalyptic 4140 21147 arithmetic 15 203 877 4140 21147 678570 4213597 astonishing 15 binomial 15 brilliant 15 cake 15 Chen 877 congruent 15 52 877 115975 4213597 constructible 15 Cunningham 15 cyclic 15 877 4213597 D-number 15 de Polignac 877 decagonal 52 deficient 15 52 203 877 21147 115975 4213597 dig.balanced 15 52 678570 190899322 double fact. 15 Duffinian 203 4213597 eban 52 economical 15 203 877 115975 emirpimes 15 203 equidigital 15 203 877 115975 evil 15 4140 21147 115975 678570 4213597 27644437 190899322 gapful 4213597 happy 203 Harshad 4140 hexagonal 15 iban 203 4140 21147 idoneal 15 inconsummate 21147 interprime 15 678570 junction 27644437 katadrome 52 Lehmer 15 lucky 15 21147 Lynch-Bell 15 magic 15 magnanimous 52 203 metadrome 15 modest 203 nialpdrome 52 877 nude 15 oban 15 877 odious 52 203 877 panconsummate 15 pandigital 15 partition 15 pernicious 52 203 877 plaindrome 15 practical 4140 prime 877 27644437 pseudoperfect 4140 678570 repunit 15 Ruth-Aaron 15 semiprime 15 203 sliding 52 sphenic 4213597 strong prime 877 tau 4140 tetranacci 15 triangular 15 uban 15 52 unprimeable 4140 untouchable 52 wasteful 52 4140 21147 678570 4213597 weak prime 27644437 Zuckerman 15 Zumkeller 4140