O'Halloran numbers

O'Halloran numbers

An even number 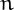$n$

$n$

is a O'Halloran number if there is not a cuboid of size 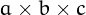$a\times b\times c$ whose surface is equal to $n$

$n$

.

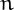In other words, O'Halloran numbers are those even numbers that cannot be expressed as $2(a\cdot b+b\cdot c + c\cdot a)$ .

There are exactly 16 such numbers, namely 8, 12, 20, 36, 44, 60, 84, 116, 140, 156, 204, 260, 380, 420, 660, and 924.

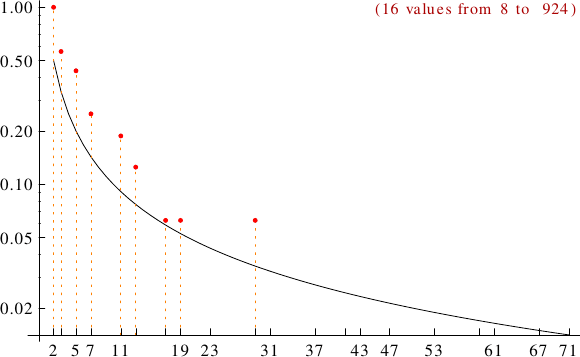
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

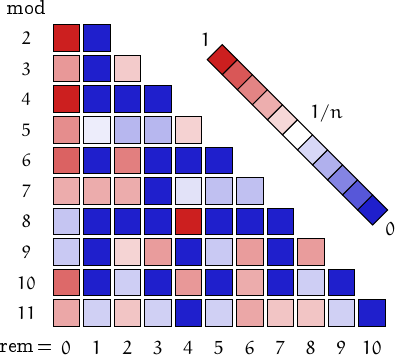
remainders of O Halloran numbers

A graph displaying how many O Halloran numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

divisibility of O Halloran numbers

Useful links OEIS, Sequence A072843

O Halloran numbers can also be... (you may click on names or numbers and on + to get more values)

aban 12 20 36 44 60 84 116 140 156 204 + 380 420 660 924 abundant 12 20 36 60 84 140 156 204 260 380 420 660 924 admirable 12 20 84 140 alternating 12 36 amenable 12 20 36 44 60 84 116 140 156 204 + 380 420 660 924 apocalyptic 660 924 arithmetic 20 44 60 116 140 204 260 380 420 660 924 astonishing 204 betrothed 140 binomial 20 36 84 924 congruent 20 60 84 116 156 260 380 660 924 constructible 12 20 60 204 deficient 44 116 dig.balanced 12 44 156 204 260 380 420 660 Duffinian 36 eban 36 44 60 eRAP 20 esthetic 12 evil 12 20 36 60 116 156 204 260 380 420 660 924 gapful 140 260 660 Gilda 660 happy 44 harmonic 140 Harshad 12 20 36 60 84 140 156 204 420 660 highly composite 12 36 60 hoax 84 660 iban 12 20 44 140 204 420 idoneal 12 60 inconsummate 84 interprime 12 60 260 420 660 924 Jordan-Polya 12 36 junction 204 420 katadrome 20 60 84 420 Lynch-Bell 12 36 magic 260 magnanimous 12 20 116 metadrome 12 36 156 Moran 84 156 nialpdrome 20 44 60 84 420 660 nonagonal 204 nude 12 36 44 oban 12 20 36 60 380 660 odious 44 84 140 palindromic 44 panconsummate 12 20 36 pandigital 156 pentagonal 12 pernicious 12 20 36 44 84 140 260 Perrin 12 plaindrome 12 36 44 116 156 power 36 powerful 36 practical 12 20 36 60 84 140 156 204 260 380 420 660 924 prim.abundant 12 20 pronic 12 20 156 380 420 pseudoperfect 12 20 36 60 84 140 156 204 260 380 420 660 924 repdigit 44 repunit 156 Saint-Exupery 60 self 20 sliding 20 square 36 straight-line 420 subfactorial 44 super Niven 12 20 36 60 140 204 420 660 superabundant 12 36 60 tau 12 36 60 84 156 204 tetrahedral 20 84 triangular 36 tribonacci 44 uban 12 20 36 60 Ulam 36 260 unprimeable 204 wasteful 12 20 36 44 60 84 116 140 156 204 + 380 420 660 924 Zuckerman 12 36 Zumkeller 12 20 60 84 140 156 204 260 380 420 660 924 zygodrome 44