Euler's idoneal numbers, are those positive integers 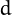 such that if
such that if 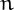 can be written in only one way as
can be written in only one way as  (where
(where  is
relatively prime to
is
relatively prime to 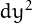 ) then
) then 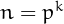 or
or 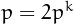 , where
, where  and
and  is a prime.
is a prime.
An equivalent simpler definition is:
a number is idoneal if and only if it cannot be written as
for
b>c>0$">.
Sometimes they are called suitable numbers or convenient numbers.
Only 65 idoneal number are known and the list is conjectured to be complete. P.Weinberger proved in 1973 that the list can contain at most one more number.
The known idoneal numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 15, 16, 18, 21, 22, 24, 25, 28, 30, 33, 37, 40, 42, 45, 48, 57, 58, 60, 70, 72, 78, 85, 88, 93, 102, 105, 112, 120, 130, 133, 165, 168, 177, 190, 210, 232, 240, 253, 273, 280, 312, 330, 345, 357, 385, 408, 462, 520, 760, 840, 1320, 1365, 1848.
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

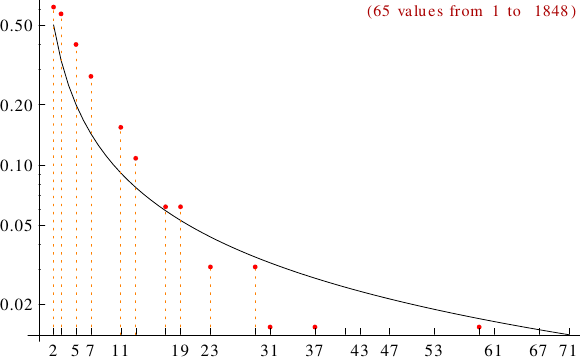
A graph displaying how many idoneal numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.
Idoneal numbers can also be... (you may click on names or numbers and on + to get more values)
a-pointer
13
ABA
18
24
72
aban
10
12
13
+
840
abundant
12
18
24
+
1848
Achilles
72
admirable
12
24
30
+
120
alternating
10
12
16
+
385
amenable
12
13
16
+
1848
apocalyptic
312
840
arithmetic
13
15
21
+
1848
astonishing
15
automorphic
25
Bell
15
betrothed
48
binomial
10
15
21
+
1365
brilliant
10
15
21
+
253
c.heptagonal
22
253
c.nonagonal
10
28
190
253
c.octagonal
25
c.pentagonal
16
c.square
13
25
85
c.triangular
10
85
760
cake
15
42
93
+
232
Catalan
42
Chen
13
37
compositorial
24
congruent
13
15
21
+
1848
constructible
10
12
15
+
408
Cullen
25
385
Cunningham
10
15
24
+
1848
Curzon
18
21
30
+
1365
cyclic
13
15
33
+
345
D-number
15
21
33
+
177
d-powerful
24
357
decagonal
10
85
232
deficient
10
13
15
+
1365
dig.balanced
10
12
15
+
520
double fact.
15
48
105
droll
72
240
Duffinian
16
21
25
+
385
eban
30
40
42
60
economical
10
13
15
+
177
emirp
13
37
emirpimes
15
58
85
+
177
equidigital
10
13
15
+
177
eRAP
24
esthetic
10
12
21
+
345
Eulerian
57
120
evil
10
12
15
+
1848
factorial
24
120
fibodiv
28
Fibonacci
13
21
Friedman
25
gapful
105
120
130
+
1365
Gilda
78
330
Giuga
30
good prime
37
happy
10
13
28
+
280
harmonic
28
Harshad
10
12
18
+
1848
heptagonal
18
112
hex
37
hexagonal
15
28
45
+
190
highly composite
12
24
48
+
840
hoax
22
58
85
Hogben
13
21
57
+
273
house
78
hyperperfect
21
28
iban
10
12
21
+
1320
iccanobiF
13
impolite
16
inconsummate
840
interprime
12
15
18
+
1320
Jacobsthal
21
85
1365
Jordan-Polya
12
16
24
+
240
junction
105
210
408
1320
Kaprekar
45
katadrome
10
21
30
+
840
Lehmer
15
85
133
Leyland
57
177
lonely
120
Lucas
18
lucky
13
15
21
+
1365
Lynch-Bell
12
15
24
+
312
magic
15
magnanimous
12
16
21
+
130
metadrome
12
13
15
+
357
modest
13
133
Moran
18
21
42
+
190
Motzkin
21
nialpdrome
10
21
22
+
840
nonagonal
24
nude
12
15
22
+
1848
O'Halloran
12
60
oban
10
12
13
+
760
octagonal
21
40
133
+
408
odious
13
16
21
+
385
palindromic
22
33
88
232
pancake
16
22
37
232
panconsummate
10
12
15
+
85
pandigital
15
21
78
+
210
partition
15
22
30
+
385
pentagonal
12
22
70
+
330
perfect
28
pernicious
10
12
13
+
520
Perrin
10
12
22
Pierpont
13
37
plaindrome
12
13
15
+
357
power
16
25
powerful
16
25
72
practical
12
16
18
+
1848
prim.abundant
12
18
30
+
102
prime
13
37
primeval
13
37
primorial
30
210
pronic
12
30
42
+
462
Proth
13
25
33
+
385
pseudoperfect
12
18
24
+
1848
repdigit
22
33
88
repfigit
28
repunit
13
15
21
+
1365
Ruth-Aaron
15
16
24
+
105
Saint-Exupery
60
self
42
165
312
+
760
self-describing
22
semiprime
10
15
21
+
253
sliding
25
70
133
520
Smith
22
58
85
sphenic
30
42
70
+
385
square
16
25
star
13
37
253
straight-line
210
345
357
840
strobogrammatic
88
strong prime
37
super Niven
10
12
24
+
1320
super-d
105
190
462
1848
superabundant
12
24
48
+
840
tau
12
18
24
+
240
tetrahedral
10
120
165
tetranacci
15
triangular
10
15
21
+
253
tribonacci
13
24
trimorphic
24
25
truncatable prime
13
37
twin
13
uban
10
12
13
+
93
Ulam
13
16
18
+
273
undulating
232
unprimeable
840
untouchable
88
120
210
+
520
upside-down
28
37
357
wasteful
12
18
22
+
1848
weak prime
13
weird
70
Zeisel
105
Zuckerman
12
15
24
+
312
Zumkeller
12
24
28
+
1848
zygodrome
22
33
88