Motzkin numbers

Motzkin numbers have many combinatorial interpretations. In particular, $M_n$

is the total number of ways in which it is possible to draw non-intersecting chords between $n$

points on a circle.

For example, for $n=7$ , it is possible to draw such chords in 127 ways. In the picture aside I display only the 16 ones which are distinct by rotation or reflection.

Motzkin numbers can be computed with the recurrence

$M_n = \frac{3(n-1)M_{n-2}+(2n+1)M_{n-1}}{n+2}\,,$

where

Several sums are know for Motzkin numbers, for example,

$M_n = \sum_{k=0}^{\lfloor n/2\rfloor}\frac{1}{k+1}{{2k}\choose k}{n\choose{2k}}\,.$

The first Motzkin numbers are 1, 2, 4, 9, 21, 51, 127, 323, 835, 2188, 5798, 15511, 41835, 113634, 310572, 853467, 2356779, 6536382 more terms

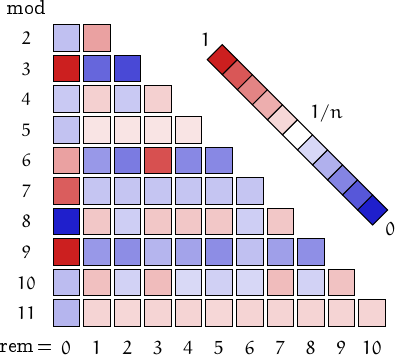
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

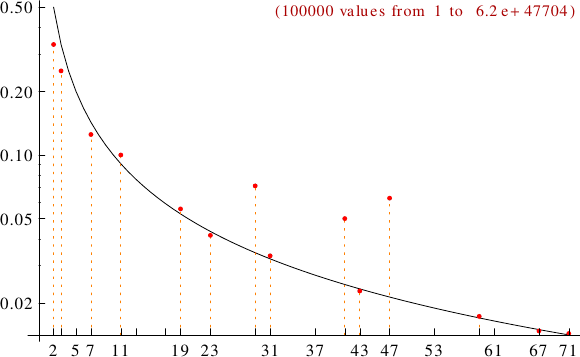
A graph displaying how many Motzkin numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Useful links Mathworld, Motzkin Number
Wikipedia, Motzkin number
OEIS, Sequence A001006

Motzkin numbers can also be... (you may click on names or numbers)

aban 21 51 127 323 835 abundant 113634 310572 6536382 18199284 admirable 6536382 alternating 21 127 323 amenable 21 2188 310572 18199284 apocalyptic 5798 15511 arithmetic 21 51 127 323 835 5798 15511 41835 113634 853467 2356779 6536382 binomial 21 brilliant 21 323 c.pentagonal 51 Chen 127 15511 congruent 21 127 323 5798 15511 6536382 constructible 51 Cunningham 127 323 2188 Curzon 21 5798 cyclic 51 127 323 835 15511 41835 853467 D-number 21 51 853467 d-powerful 2356779 de Polignac 127 deficient 21 51 127 323 835 2188 5798 15511 41835 853467 2356779 dig.balanced 21 835 41835 Duffinian 21 323 835 economical 21 127 15511 emirp 15511 emirpimes 51 835 equidigital 21 127 15511 esthetic 21 323 evil 51 323 2188 310572 50852019 142547559 fibodiv 323 Fibonacci 21 Friedman 127 gapful 1129760415 good prime 127 happy 2188 5798 Harshad 21 113634 310572 hex 127 Hogben 21 hyperperfect 21 iban 21 127 323 idoneal 21 inconsummate 310572 interprime 21 Jacobsthal 21 junction 15511 katadrome 21 51 Lehmer 51 lucky 21 51 127 15511 2356779 magnanimous 21 metadrome 127 Moran 21 nialpdrome 21 51 oban 323 835 octagonal 21 odious 21 127 835 5798 15511 41835 113634 853467 2356779 6536382 18199284 400763223 palindromic 323 panconsummate 21 127 pandigital 21 41835 pentagonal 51 pernicious 21 127 835 5798 113634 853467 2356779 Perrin 51 plaindrome 127 2356779 prim.abundant 6536382 prime 127 15511 pseudoperfect 113634 310572 repunit 21 127 self 323 5798 142547559 semiprime 21 51 323 835 853467 sphenic 5798 41835 6536382 strong prime 127 super-d 127 15511 tau 310572 18199284 triangular 21 trimorphic 51 uban 21 51 undulating 323 unprimeable 2188 41835 113634 untouchable 5798 113634 wasteful 51 323 835 2188 5798 41835 113634 310572 853467 2356779 6536382 weak prime 15511 Woodall 323