Also known as 3-Knödel numbers, they are number 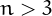 3$"> such that
3$"> such that
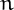 divides
divides  for all
for all 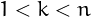 relatively prime to
relatively prime to 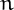 .
.
For example, 9 is a D-number since it divides all the numbers
,
,
,
and
.
The smallest 3 × 3 magic square whose entries are D-numbers is
| 87 | 267 | 69 |
| 123 | 141 | 159 |
| 213 | 15 | 195 |
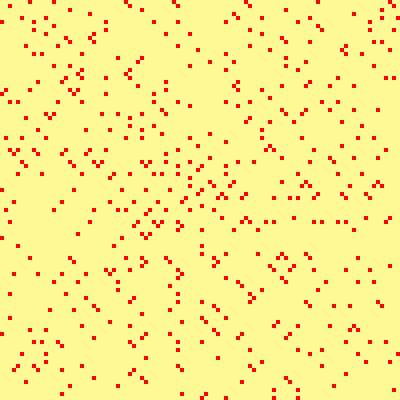
Below, the spiral pattern of D-numbers up to . See the page on prime numbers for an explanation and links to similar pictures.
The first D-numbers are 9, 15, 21, 33, 39, 51, 57, 63, 69, 87, 93, 111, 123, 129, 141, 159, 177, 183, 195, 201, 213, 219 more terms
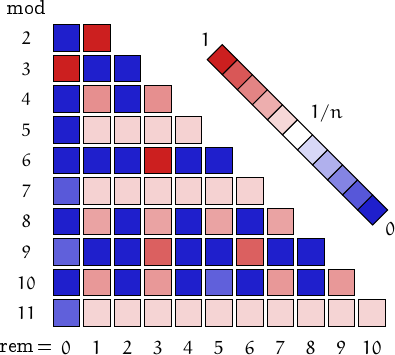
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
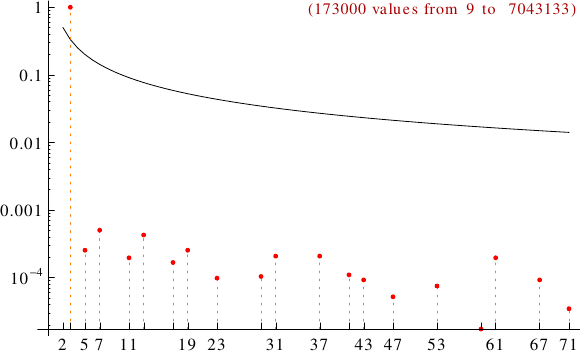
A graph displaying how many D-numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.
D-numbers can also be... (you may click on names or numbers and on + to get more values)
aban
15
21
33
39
+
7000989
abundant
4095
16695
1527435
2475795
+
6310395
admirable
4095
alternating
21
63
69
87
+
7038723
amenable
21
33
57
69
+
7043133
apocalyptic
411
669
693
723
+
29919
arithmetic
15
21
33
39
+
7043133
astonishing
15
Bell
15
betrothed
195
binomial
15
21
1953
3003
+
5572791
brilliant
15
21
c.pentagonal
51
141
681
951
+
7018251
cake
15
93
congruent
15
21
39
63
+
7043133
constructible
15
51
771
196611
Cullen
2049
Cunningham
15
33
63
129
+
7011903
Curzon
21
33
69
141
+
7042569
cyclic
15
33
51
69
+
7043109
d-powerful
63
267
849
2283
+
7040589
de Polignac
7431
8031
11541
17229
+
7042281
deficient
15
21
33
39
+
7043133
dig.balanced
15
21
141
177
+
7043079
double fact.
15
Duffinian
21
39
57
63
+
7043133
economical
15
21
111
123
+
2999949
emirpimes
15
39
51
93
+
7042731
equidigital
15
21
111
123
+
2999949
esthetic
21
87
123
321
+
5454321
Eulerian
57
1191
4083
evil
15
33
39
51
+
7043133
fibodiv
183
2733
3903
9267
+
4788039
Fibonacci
21
Friedman
15567
15627
16347
16743
+
995331
gapful
195
315
693
1443
+
6999363
happy
129
219
291
921
+
7042773
Harshad
21
63
111
195
+
6727539
heptagonal
21483
hexagonal
15
3003
hoax
24963
178923
226083
334971
+
3827043
Hogben
21
57
111
183
+
6993381
house
933
7617
hyperperfect
21
iban
21
111
123
141
+
777477
iccanobiF
39
idoneal
15
21
33
57
+
177
inconsummate
63
195
381
411
+
999993
insolite
111
interprime
15
21
39
69
+
7042323
Jacobsthal
21
junction
111
303
309
315
+
7042227
katadrome
21
51
63
87
+
987621
Lehmer
15
51
771
196611
Leyland
57
177
131361
423393
lonely
31431
370317
Lucas
123
843
271443
lucky
15
21
33
51
+
7043109
Lynch-Bell
15
315
1935
magic
15
111
magnanimous
21
metadrome
15
39
57
69
+
2346789
modest
39
69
111
309
+
7023333
Moran
21
63
111
195
+
2000001
Motzkin
21
51
853467
nialpdrome
21
33
51
63
+
6666531
nonagonal
111
nude
15
33
111
315
+
3313131
oban
15
33
39
57
+
993
octagonal
21
odious
21
69
87
93
+
7042881
palindromic
33
111
141
303
+
7023207
panconsummate
15
21
39
57
+
267
pandigital
15
21
141
177
+
799899
partition
15
pentagonal
51
pernicious
21
33
69
87
+
7042881
Perrin
39
51
1497
1983
+
2240877
plaindrome
15
33
39
57
+
6667779
prim.abundant
4095
16695
Proth
33
57
129
177
+
6987777
pseudoperfect
4095
16695
repdigit
33
111
repfigit
7647
repunit
15
21
57
63
+
6993381
Ruth-Aaron
15
1683
8463
1040403
Sastry
183
self
411
501
591
681
+
7042773
semiprime
15
21
33
39
+
7043133
Smith
1935
24963
178923
226083
+
2215983
sphenic
195
399
1023
1443
+
7011903
straight-line
111
123
159
321
+
876543
strobogrammatic
69
111
6009
68889
+
6911169
super-d
69
219
339
381
+
7042881
tetranacci
15
10671
283953
triangular
15
21
1953
3003
+
5572791
trimorphic
51
249
501
5001
+
500001
uban
15
21
33
39
+
7000041
Ulam
57
69
87
177
+
7042683
undulating
141
303
393
717
+
3737373
unprimeable
10815
188235
1527435
1700415
+
6340995
upside-down
159
753
951
112899
+
994611
wasteful
33
39
51
57
+
7043133
Wieferich
3279
10533
Woodall
63
159
1023
10239
Zuckerman
15
111
315
13113
Zumkeller
4095
16695
zygodrome
33
111
11199
22233
+
6666999