The double factorial of an integer 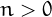 0$">, denoted by
0$">, denoted by 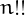 , is the product of all the integers from 1 to
, is the product of all the integers from 1 to 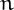 which have the same parity as
which have the same parity as 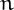 .
By definition,
.
By definition, 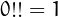 . The double factorial is not to be confused with
the double application of factorial, i.e.
. The double factorial is not to be confused with
the double application of factorial, i.e.  .
.
For example, and
.
The first double factorials are 1, 2, 3, 8, 15, 48, 105, 384, 945, 3840, 10395, 46080, 135135, 645120, 2027025, 10321920, 34459425 more terms
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

A graph displaying how many double factorials are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Double factorials can also be... (you may click on names or numbers)
ABA
384
aban
15
48
105
384
945
abundant
48
384
945
3840
10395
46080
135135
645120
2027025
10321920
34459425
admirable
945
alternating
105
945
amenable
48
105
384
945
3840
46080
645120
2027025
10321920
34459425
185794560
apocalyptic
384
3840
10395
arithmetic
15
105
945
10395
135135
645120
astonishing
15
Bell
15
betrothed
48
binomial
15
105
brilliant
15
cake
15
congruent
15
384
3840
10395
46080
135135
645120
constructible
15
48
384
3840
Cunningham
15
48
Curzon
105
34459425
cyclic
15
D-number
15
deficient
15
105
dig.balanced
15
384
10395
economical
15
105
384
3840
10321920
emirpimes
15
equidigital
15
105
384
3840
evil
15
48
105
384
945
3840
46080
135135
645120
2027025
10321920
34459425
185794560
frugal
10321920
185794560
gapful
105
3840
10395
46080
135135
645120
2027025
10321920
34459425
185794560
654729075
3715891200
13749310575
81749606400
happy
135135
645120
2027025
Harshad
48
3840
46080
645120
10321920
185794560
654729075
3715891200
hexagonal
15
highly composite
48
idoneal
15
48
105
inconsummate
945
interprime
15
105
3840
10395
Jordan-Polya
48
384
3840
46080
645120
10321920
185794560
3715891200
81749606400
1961990553600
51011754393600
junction
105
645120
2027025
10321920
Lehmer
15
Leyland
945
lucky
15
105
135135
Lynch-Bell
15
48
384
magic
15
metadrome
15
48
nude
15
48
384
135135
oban
15
odious
10395
654729075
panconsummate
15
pandigital
15
partition
15
pernicious
48
384
10395
plaindrome
15
48
practical
48
384
3840
46080
645120
prim.abundant
945
pseudoperfect
48
384
945
3840
10395
46080
135135
645120
repunit
15
Ruth-Aaron
15
105
Saint-Exupery
3840
3715891200
self
34459425
654729075
semiprime
15
sphenic
105
super Niven
48
super-d
105
135135
superabundant
48
tau
384
645120
10321920
tetranacci
15
triangular
15
105
uban
15
48
Ulam
48
46080
unprimeable
46080
645120
wasteful
48
945
10395
46080
135135
645120
2027025
Zeisel
105
Zuckerman
15
384
Zumkeller
48
384
945
3840
10395
46080