Perrin numbers

Perrin numbers

Perrin numbers are members of the sequence defined by the recurrence 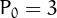$P_0=3$

$P_0=3$

,

$P_1=0$

,

$P_2=2$

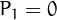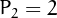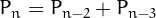and $P_n=P_{n-2}+P_{n-3}$ for

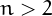2$">.

The first terms of the Perrin sequence are 3, 0, 2, 3, 2, 5, 5, 7, 10, 12, 17, 22, 29, 39, 51, 68, 90, 119, 158, 209, 277, 367, 486, 644 more terms

Lucas proved that if $p$ is a prime number, then $p$ divides $P_p$ .

The composites that show the same behaviour are quite rare and are called Perrin pseudoprimes. The first are 271441, 904631, 16532714, 24658561, 27422714, 27664033, 46672291, 102690901, 130944133, 196075949.

Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

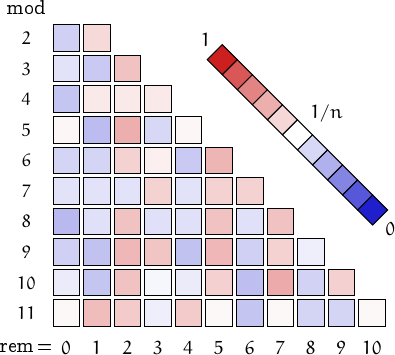
remainders of Perrin numbers

A graph displaying how many Perrin numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

divisibility of Perrin numbers

Useful links Mathworld, Perrin Sequence
Wikipedia, Perrin@ number
OEIS, Sequence A001608 Perrin sequence
OEIS, Sequence A013998 Perrin pseudoprimes

Perrin numbers can also be... (you may click on names or numbers and on + to get more values)

aban 10 12 17 22 + 486 644 853 abundant 12 90 486 644 + 57918 76725 2968530 admirable 12 644 alternating 10 12 29 90 367 6107 76725 amenable 12 17 29 68 + 114853953 201554637 468557684 apocalyptic 1497 2627 3480 6107 + 14197 18807 24914 arithmetic 17 22 29 39 + 5209407 6900995 9141872 binomial 10 brilliant 10 209 2627 c.heptagonal 22 c.nonagonal 10 c.pentagonal 51 c.triangular 10 Chen 17 29 14197 43721 congruent 22 29 39 119 + 2240877 5209407 9141872 constructible 10 12 17 51 68 Cunningham 10 17 3480 Curzon 29 90 158 209 4610 43721 57918 cyclic 17 29 51 119 + 549289 3932465 6900995 D-number 39 51 1497 1983 18807 727653 2240877 d-powerful 209 2627 24914 decagonal 10 deficient 10 17 22 29 + 5209407 6900995 9141872 dig.balanced 10 12 209 3480 43721 727653 Duffinian 39 119 209 1497 + 727653 963935 2240877 economical 10 17 29 119 + 3932465 12110402 16042867 emirp 17 emirpimes 39 51 158 1497 + 18807 12110402 37295141 equidigital 10 17 29 119 + 3932465 12110402 16042867 eRAP 236282 esthetic 10 12 evil 10 12 17 29 + 468557684 620706778 822261415 gapful 1130 3480 76725 86700684 3354494070 5886726725 Gilda 29 good prime 17 29 853 happy 10 68 367 644 + 43721 313007 2968530 Harshad 10 12 90 209 + 3480 963935 5209407 highly composite 12 hoax 22 644 hungry 17 iban 10 12 17 22 277 10717 43721 iccanobiF 39 idoneal 10 12 22 inconsummate 486 1497 1983 4610 + 18807 236282 313007 interprime 12 39 1983 2627 + 10717 76725 2240877 Jordan-Polya 12 junction 4610 6107 313007 963935 2968530 37295141 49405543 katadrome 10 51 90 853 Lehmer 51 Leyland 17 Lucas 29 lucky 51 367 1497 1983 727653 Lynch-Bell 12 magnanimous 12 29 158 209 1130 metadrome 12 17 29 39 68 158 367 modest 29 39 209 8090 Moran 209 963935 Motzkin 51 nialpdrome 10 22 51 90 644 853 nude 12 22 O'Halloran 12 oban 10 12 17 29 + 90 367 853 odious 22 158 367 644 + 28153269 49405543 86700684 palindromic 22 pancake 22 29 277 14197 panconsummate 10 12 39 partition 22 pentagonal 12 22 51 pernicious 10 12 17 22 + 1276942 5209407 9141872 Pierpont 17 plaindrome 12 17 22 29 + 158 277 367 practical 12 90 486 644 3480 57918 2968530 prim.abundant 12 644 76725 prime 17 29 277 367 + 14197 43721 1442968193 pronic 12 90 Proth 17 209 pseudoperfect 12 90 486 644 3480 57918 76725 repdigit 22 self 209 277 367 10717 + 101639 414646 727653 self-describing 22 semiprime 10 22 39 51 + 21252274 37295141 49405543 sliding 29 Smith 22 Sophie Germain 29 43721 sphenic 1130 4610 8090 101639 + 3932465 16042867 65448410 strong prime 17 29 277 367 853 14197 super Niven 10 12 90 super-d 119 2627 3480 10717 1691588 3932465 superabundant 12 tau 12 tetrahedral 10 tetranacci 29 triangular 10 trimorphic 51 truncatable prime 17 29 367 853 twin 17 29 uban 10 12 17 22 + 51 68 90 Ulam 209 6107 236282 unprimeable 1130 3480 4610 33004 + 1691588 3932465 6900995 wasteful 12 22 39 51 + 5209407 6900995 9141872 weak prime 43721 Woodall 17 Zuckerman 12 Zumkeller 12 90 486 644 3480 57918 76725 zygodrome 22