Koordinatni sistem

Koordinátni sistém je v geometriji sistem, ki uporablja eno ali več števil ali koordinat za enolično določanje položaja točk ali drugih geometrijskih elementov na mnogoterosti, kot je evklidski prostor.[1][2] Vrstni red koordinat je pomemben in jih včasih prepoznamo po položaju v urejeni terki (urejeni par), včasih pa po črki, kot " x -koordinata". Koordinate so v elementarni matematiki realna števila, lahko pa so tudi kompleksna števila ali elementi bolj abstraktnega sistema, kot je komutativni kolobar. Uporaba koordinatnega sistema omogoča, da se geometrijski problemi prevedejo v probleme o številih in obratno; to je osnova analitične geometrije.[3]
Vrste koordinatnih sistemov
[uredi | uredi kodo]Številska premica
[uredi | uredi kodo]Najpreprostejši primer koordinatnega sistema je določitev koordinate točke na premici z realnimi števili s pomočjo številske premice. Številsko premico imenujemo tudi koordinatna os. V tem sistemu je na podani premici izbrana točka O (koordinatno izhodišče), ki je slika števila 0. Točki P smo priredili število 1. Dolžina daljice OP predstavlja enoto na številski premici. Vsaka točka na premici je slika enega samega realnega števila. Celotna številska premica je potem slika vseh realnih števil. Dolžina enote določa razdaljo med ostalimi slikami števil. Večja enota pomeni večjo oddaljenost med drugimi števili. Vsaka točka na številski premici ima natanko določeno koordinato in vsako realno število je koordinata unikatne točke.[4]

Kartezični ali pravokotni koordinatni sistem
[uredi | uredi kodo]
Prototipni primer koordinatnega sistema je kartezični koordinatni sistem. V ravnini izberemo dve pravokotni črti in koordinate točke, ki so razdalje te točke od dveh koordinatnih osi.

V treh dimenzijah so izbrane tri medsebojno ortogonalne ravnine in tri koordinate točke so označene razdalje do vsake ravnine.[5] Točko v tridimenzionalnem koordinatnem sistemu definiramo kot P (x, y, z), kjer vsak od treh parametrov pomeni projekcijo na eno izmed treh osi.
Odvisno od smeri in vrstnega reda koordinatnih osi je lahko tridimenzionalni sistem desni ali levi.
Polarni koordinatni sistem
[uredi | uredi kodo]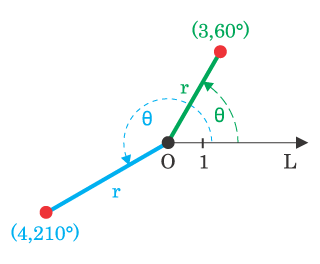
Drug pogost koordinatni sistem v ravnini je polarni koordinatni sistem [6] Izbrana točka se imenuje pol, poltrak od te točke pa polarna os. Polarni kot θ je kot med daljico med koordinatnim izhodiščem in točko ter polarno osjo (merjeno v nasprotni smeri urinega kazalca od osi do daljice). Na daljici je unikatna točka z oddaljenostjo r od izhodišča. Za dani par koordinat (r ,θ) obstaja ena sama točka, vendar je vsaka točka predstavljena z mnogimi pari koordinat. Na primer (r,θ), (r,θ+2π) in (-r,θ+π) so vse polarne koordinate za isto točko. Pol je predstavljen z (0,θ) za katero koli vrednost θ.
Cilindrični in sferni koordinatni sistem
[uredi | uredi kodo]
Obstajata dve splošni metodi za razširitev polarnega koordinatnega sistema na tri dimenzije. Cilindrični koordinatni sistem je prostorski, ki ga dobimo tako, da polarnemu dodamo še eno koordinato - višino nad ali pod osnovno ravnino. Točka je tako določena s tremi števili (r,θ,z).[7] Sferni koordinatni sistem je krivočrtni sistem koordinat v trirazsežnem prostoru, s pomočjo katerega enolično določimo lego točk na krogli ali sferoidu. Pretvorba para cilindričnih koordinat (r,z) v polarne koordinate (ρ,φ ) daje trojno (ρ,θ,φ).[8]
Homogeni koordinatni sistem
[uredi | uredi kodo]Točka na ravnini je lahko v homogenih koordinatah predstavljena s trojko (x,y,z) kjer sta x/z in y/z kartezični koordinati točke.[9] To uvede "dodatno" koordinato, saj sta za določitev točke na ravnini potrebni le dve, vendar je ta sistem uporaben, ker predstavlja katero koli točko na projektivni ravnini brez uporabe neskončnosti. Na splošno je homogeni koordinatni sistem tisti, kjer so pomembna le razmerja koordinat in ne dejanske vrednosti.
Drugi pogosto uporabljeni koordinatni sistemi
[uredi | uredi kodo]Nekateri drugi koordinatni sistemi so:
- geografski koordinatni sistem
- nebesni koordinatni sistem
- inercialni opazovalni sistem
- trilinearni koordinatni sistem
- težiščni koordinatni sistem
Koordinate geometrijskih objektov
[uredi | uredi kodo]Koordinatni sistemi se pogosto uporabljajo za določanje položaja točke, lahko pa se uporabljajo tudi za določanje položaja bolj zapletenih likov, kot so premice, ravnine, krožnic ali sfer. Na primer, Plückerjeve koordinate se uporabljajo za določanje položaja premic v vesolju.[10] Kadar obstaja potreba, se vrsta lika, ki se ga opisuje, uporablja za razlikovanje vrste koordinatnega sistema, na primer izraz koordinate premice se uporablja za kateri koli koordinatni sistem, ki določa položaj premice.
Sklici
[uredi | uredi kodo]- ↑ Woods p. 1
- ↑ Weisstein, Eric Wolfgang. »Coordinate System«. MathWorld.
- ↑ Weisstein, Eric Wolfgang. »Coordinates«. MathWorld.
- ↑ Stewart, James B.; Redlin, Lothar; Watson, Saleem (2008). College Algebra (5th izd.). Brooks Cole. str. 13–19. ISBN 978-0-495-56521-5.
- ↑ »Rectangular Coordinates (x, y, z)«. Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd, 3rd print izd.). New York: Springer-Verlag. 1988. str. 9–11 (Table 1.01). ISBN 978-0-387-18430-2.
- ↑ Finney, Ross; George Thomas; Franklin Demana; Bert Waits (Junij 1994). Calculus: Graphical, Numerical, Algebraic (Single Variable Version izd.). Addison-Wesley Publishing Co. ISBN 0-201-55478-X.
- ↑ Margenau, Henry; Murphy, George M. (1956). The Mathematics of Physics and Chemistry. New York City: D. van Nostrand. str. 178. ISBN 978-0-88275-423-9. LCCN 55010911. OCLC 3017486.
- ↑ Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. str. 658. ISBN 0-07-043316-X. LCCN 52011515.
- ↑ Jones, Alfred Clement (1912). An Introduction to Algebraical Geometry. Clarendon.
- ↑ Hodge, W.V.D.; D. Pedoe (1994) [1947]. Methods of Algebraic Geometry, Volume I (Book II). Cambridge University Press. ISBN 978-0-521-46900-5.
Viri
[uredi | uredi kodo]- Voitsekhovskii, M.I.; Ivanov, A.B. (2001) [1994]. »Coordinates«. Encyclopedia of Mathematics. EMS Press.
- Woods, Frederick S. (1922). Higher Geometry. Ginn and Co. str. 1ff.
- Shigeyuki Morita; Teruko Nagase; Katsumi Nomizu (2001). Geometry of Differential Forms. AMS Bookstore. str. 12. ISBN 0-8218-1045-6.