Torus

 

Kao takva ploha torus ima "rupu". Ako označimo sa c radijus od centra "rupe" do centra torusa, a sa a radijus torusa dolazimo do njegove parametarske jednačine:

${\displaystyle {\begin{cases}x=(c+acosv)cosu\\y=(c+acosv)sinu\\z=asinv\end{cases}}}$  za ${\displaystyle u,v\in [0,2\pi )}$  ^[1]

gdje su ${\displaystyle u}$  i ${\displaystyle v}$  uglovi koji čine puni krug, tako da njihove vrijednosti počinju i završavaju u istoj tački

${\displaystyle c}$  je udaljenost od centra cijevi do središta torusa, ${\displaystyle a}$  je promjer cijevi. ${\displaystyle c}$  je glavni radijus, a ${\displaystyle a}$  sporedni radijus.

Implicitna jednačina u Kartezijevim koordinatama je

${\displaystyle \left(c-{\sqrt {x^{2}+y^{2}}}\right)^{2}+z^{2}=a^{2},}$ 

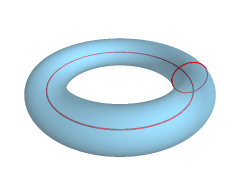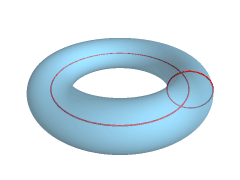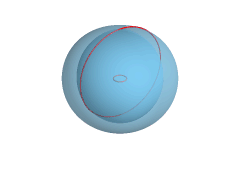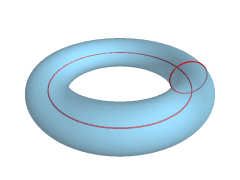
Površina torusa je

${\displaystyle P=\left(2\pi r\right)\left(2\pi R\right)=4\pi ^{2}ca}$ ^[2][3]

a zapremina

${\displaystyle V=\left(\pi a^{2}\right)\left(2\pi c\right)=2\pi ^{2}ca^{2}}$ 

${\displaystyle \ V=2\pi ^{2}Rr^{2},}$ 

Dokaz

 

${\displaystyle \ S=S_{1}-S_{2},}$ 

${\displaystyle \ S_{1}=\pi (R+a)^{2},}$ 

${\displaystyle \ S_{2}=\pi (R-a)^{2}}$ 

Prema Pitagorinoj teoremi imamo

${\displaystyle \ a={\sqrt {r^{2}-z^{2}}}}$ 

${\displaystyle \ S_{1}=\pi (R+{\sqrt {r^{2}-z^{2}}})^{2}}$ 
${\displaystyle \ S_{2}=\pi (R-{\sqrt {r^{2}-z^{2}}})^{2}}$ 

${\displaystyle \ S=\pi (R+{\sqrt {r^{2}-z^{2}}})^{2}-\pi (R-{\sqrt {r^{2}-z^{2}}})^{2}}$ 

${\displaystyle \ S=\pi [(R+{\sqrt {r^{2}-z^{2}}})^{2}-(R-{\sqrt {r^{2}-z^{2}}})^{2}]}$ 

${\displaystyle \ S=\pi (R^{2}+2R{\sqrt {r^{2}-z^{2}}}+r^{2}-z^{2}-R^{2}+2R{\sqrt {r^{2}-z^{2}}}-r^{2}+z^{2})}$ 

${\displaystyle \ S=\pi (2R{\sqrt {r^{2}-z^{2}}}+2R{\sqrt {r^{2}-z^{2}}})}$ 

${\displaystyle \ S=4\pi R{\sqrt {r^{2}-z^{2}}}}$ 

${\displaystyle \ V=\int \limits _{-r}^{r}S(z)\,dz}$ 

${\displaystyle \ V=\int \limits _{-r}^{r}4\pi R{\sqrt {r^{2}-z^{2}}}\,dz}$ 

${\displaystyle \ V=4\pi R\int \limits _{-r}^{r}{\sqrt {r^{2}-z^{2}}}\,dz}$ 

${\displaystyle \ \int \limits _{-r}^{r}{\sqrt {r^{2}-z^{2}}}\,dz}$ 

${\displaystyle \ {du \over dz}={d{\sqrt {r^{2}-z^{2}}} \over dz}}$ 

${\displaystyle {d{\sqrt {r^{2}-z^{2}}} \over dz}{d(r^{2}-z^{2}) \over d(r^{2}-z^{2})}}$ 

${\displaystyle {d{\sqrt {r^{2}-z^{2}}} \over d(r^{2}-z^{2})}{d(r^{2}-z^{2}) \over dz}}$ 

${\displaystyle \ {du \over dz}={1 \over 2(r^{2}-z^{2})}({dr^{2} \over dz^{2}}-{dz^{2} \over dz})={1 \over 2(r^{2}-z^{2})}(0-2z)={-2z \over 2(r^{2}-z^{2})}=-{z \over (r^{2}-z^{2})}}$ 

${\displaystyle \ du=-{z \over r^{2}-z^{2}}dz}$ 

${\displaystyle \ \int \limits _{-r}^{r}{\sqrt {r^{2}-z^{2}}}\,dz=z{\sqrt {r^{2}-z^{2}}}{\bigg |}_{-r}^{r}-\int \limits _{-r}^{r}-{z^{2} \over {\sqrt {r^{2}-z^{2}}}}dz}$ 

${\displaystyle \ \int \limits _{-r}^{r}{\sqrt {r^{2}-z^{2}}}\,dz=z{\sqrt {r^{2}-z^{2}}}{\bigg |}_{-r}^{r}-\int \limits _{-r}^{r}{-z^{2}-r^{2}+r^{2} \over {\sqrt {r^{2}-z^{2}}}}dz}$ 

${\displaystyle \ \int \limits _{-r}^{r}{\sqrt {r^{2}-z^{2}}}\,dz=z{\sqrt {r^{2}-z^{2}}}{\bigg |}_{-r}^{r}-\int \limits _{-r}^{r}{r^{2}-z^{2} \over {\sqrt {r^{2}-z^{2}}}}dz+\int \limits _{-r}^{r}{r^{2} \over {\sqrt {r^{2}-z^{2}}}}dz}$ 

${\displaystyle \ \int \limits _{-r}^{r}{\sqrt {r^{2}-z^{2}}}\,dz=z{\sqrt {r^{2}-z^{2}}}{\bigg |}_{-r}^{r}-\int \limits _{-r}^{r}{\sqrt {r^{2}-z^{2}}}dz+r^{2}\int \limits _{-r}^{r}{1 \over {\sqrt {r^{2}-z^{2}}}}dz}$ 

${\displaystyle \ \int \limits _{-r}^{r}{\sqrt {r^{2}-z^{2}}}\,dz+\int \limits _{-r}^{r}{\sqrt {r^{2}-z^{2}}}\,dz=z{\sqrt {r^{2}-z^{2}}}{\bigg |}_{-r}^{r}+r^{2}\int \limits _{-r}^{r}{1 \over {\sqrt {r^{2}(1-{z^{2} \over r^{2}})}}}dz}$ 

${\displaystyle \ 2\int \limits _{-r}^{r}{\sqrt {r^{2}-z^{2}}}\,dz=z{\sqrt {r^{2}-z^{2}}}{\bigg |}_{-r}^{r}+r^{2}\int \limits _{-r}^{r}{1 \over {\sqrt {(1-({z \over r})^{2})}}}d({z \over r})}$ 

${\displaystyle \ \int \limits _{-r}^{r}{\sqrt {r^{2}-z^{2}}}\,dz={z{\sqrt {r^{2}-z^{2}}}+r^{2}\arcsin({z \over r}) \over 2}{\bigg |}_{-r}^{r}}$ 

${\displaystyle \ \int \limits _{-r}^{r}{\sqrt {r^{2}-z^{2}}}\,dz={r{\sqrt {r^{2}-r^{2}}}+r^{2}\arcsin({r \over r}) \over 2}-{-r{\sqrt {r^{2}-(-r)^{2}}}+r^{2}\arcsin({(-r) \over r}) \over 2}}$ 

${\displaystyle \ \int \limits _{-r}^{r}{\sqrt {r^{2}-z^{2}}}\,dz={r^{2}\arcsin({1})-r^{2}\arcsin({-1}) \over 2}}$ 

${\displaystyle \ \int \limits _{-r}^{r}{\sqrt {r^{2}-z^{2}}}\,dz={r^{2} \over 2}({\pi \over 2}-(-{\pi \over 2}))}$ 

${\displaystyle \ \int \limits _{-r}^{r}{\sqrt {r^{2}-z^{2}}}\,dz={r^{2}\pi \over 2}}$ 

${\displaystyle \ V=4\pi R\int \limits _{-r}^{r}{\sqrt {r^{2}-z^{2}}}\,dz\to V=4\pi R{r^{2}\pi \over 2}}$ 

${\displaystyle \ V=2\pi ^{2}Rr^{2},}$ 

Parametarska jednačina prstenastog torusa je

${\displaystyle {\begin{cases}x=(c+acosv)cosu\\y=(c+acosv)sinu\\z=asinv\end{cases}}}$ 

za ${\displaystyle u,v\in [0,2\pi )}$  ${\displaystyle ia>c}$ 

Koficienti prve kvadratne forme su

${\displaystyle E=(c+acosv)^{2}}$ 

${\displaystyle F=0}$ 

${\displaystyle G=a^{2}}$ 

dok za koeficiente druge kvadratne forme dobijamo

${\displaystyle L=-(c+acosv)cosv}$ 

${\displaystyle M=0}$ 

${\displaystyle N=-a}$ 

Gausova i srednja kriva su date sa:

${\displaystyle K_{G}={\frac {cosv}{a(c+acosv)}}}$ 

${\displaystyle K_{S}={\frac {-c+2acosv}{2a(c+acosv)}}}$ 

Uzimajući u jednačini

${\displaystyle {\begin{cases}x=(c+acosv)cosu\\y=(c+acosv)sinu\\z=asinv\end{cases}}}$ 

da je ${\displaystyle c=a}$  dobijamo parametarsku jednačinu rog torusa ^[4]

${\displaystyle {\begin{cases}x=a(1+cosv)cosu\\y=a(1+cosv)sinu\\z=asinv\end{cases}}}$ 

Za koeficiente prve kvadratne forme dobijamo:

${\displaystyle E=4a^{2}cos^{4}({\frac {1}{2}}v)}$ 

${\displaystyle F=0}$ 

${\displaystyle G=a^{2}}$ 

dok su koeficienti druge kvadratne forme rog torusa:

${\displaystyle L=-2acos^{2}({\frac {1}{2}})cosv}$ 

${\displaystyle M=0}$ 

${\displaystyle N=-a}$ 

Kod vretenastog torusa parametarska jednačina, formule za koeficiente prve i druge kvadratne forme i formule za izračunavanje srednje i Gausove krive su iste kao i kod prstenastog torusa, uz uslov ${\displaystyle c<a}$ .

Rotacione površi i njihova vizuelizacija u programskom paketu Mathematica Niš, novembar 2013.^{[mrtav link]}

1. ↑ „parametarska jednačina 06. juli 1995”. Arhivirano iz originala na datum 2019-05-20. Pristupljeno 2016-05-01. 
2. ↑ ring torus
3. ↑ površina torusa
4. ↑ Horn torus Niš novembar 2013^{[mrtav link]}