Paraboloide

Em matemática, um paraboloide é uma superfície quádrica de tipo especial. Existem dois tipos de paraboloides: elípticas e hiperbólicas.

O paraboloide elíptico é moldado como um copo de forma oval e pode ter um ponto máximo ou mínimo. Em um sistema de coordenadas apropriado, com os três eixos ${\displaystyle x}$, ${\displaystyle y}$, e ${\displaystyle z}$, podem ser representados pela equação^[1]

${\displaystyle {\frac {z}{c}}={\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}}$

onde ${\displaystyle a}$ e ${\displaystyle b}$ são constantes que determinam o grau de curvatura nos planos ${\displaystyle x}$-${\displaystyle z}$ e ${\displaystyle y}$-${\displaystyle z}$ respectivamente. Este é um parabolóide elíptico, que abre para cima.

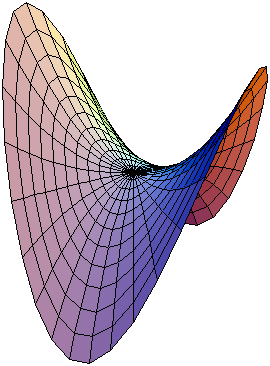
O paraboloide hiperbólico (não deve ser confundido com um hiperboloide) é uma superfície duplamente determinada em forma de sela. Em um sistema de coordenadas apropriado, um paraboloide hiperbólico pode ser representado pela equação^[2]

${\displaystyle {\frac {z}{c}}={\frac {y^{2}}{b^{2}}}-{\frac {x^{2}}{a^{2}}}.}$

Por c>0, isto é um paraboloide hiperbólico que se abre para baixo ao longo do eixo X e ao longo do eixo dos y (ou seja, a parábola no plano x=0 é aberta para cima e a parábola no plano y=0 abre-se para baixo).

Existem dois tipos de paraboloides: elíptico e hiperbólico. O paraboloide elíptico possui um formato semelhante a uma taça e pode possuir um ponto máximo ou mínimo. O paraboloide hiperbólico possui um formato semelhante a uma sela e pode possuir um ponto crítico chamado de ponto de sela. Esta é uma superfície com regras duplas.

Com a = b um paraboloide elíptico é um paraboloide de revolução: uma superfície obtida através da rotação de uma parábola ao redor de seu eixo. Este é o formato do refletor parabólico utilizado nos espelhos, antenas e objetos semelhantes. Esta superfície é também chamada de paraboloide circular.

Uma fonte de luz posicionada no ponto focal desta superfície produz um raio de luz paralelo. Isto também funciona da maneira inversa: um feixe de luz com raios paralelos incidente no paraboloide é concentrado no ponto focal. Isto também se aplica a outras ondas, como nas antenas parabólicas.

Um exemplo do quotidiano de um paraboloide hiperbólico é o formato de uma batata Pringles. O paraboloide hiperbólico é uma superfície duplamente regrada, ou seja, por cada ponto da superfície passam duas retas totalmente contidas na superfície.

• Elipsoide
• Hiperboloide
• Parábola