対流
対流(たいりゅう、英語: convection)とは、流体において温度や表面張力などが原因により不均質性が生ずるため、その内部で重力によって引き起こされる流動が生ずる現象である。
地球の大気においては、大気の鉛直方向の運動は高度 0 キロメートルから約 11 キロメートルの層に限られ、この領域を対流圏と呼ぶ。また地球や惑星の内部では、対流により内部の熱源から地表面への熱輸送が生じており、地表面の変動を引き起こす原因となっている。
近年、計算機の性能が向上し、流体の運動方程式(ナビエ-ストークスの式)を高精度に計算することが可能となったため、コンピュータを用いたシミュレーションによる対流現象の研究が盛んに行われており、工学的な技術としても重要な分野である。また惑星内部の対流など、実験・観測が不可能な領域における流体の挙動を理論的に解明する研究も行われている。
鉛直対流
編集上層ほど密度の大きな流体が静力学的不安定となり、流体の運動が生ずる対流を鉛直対流と呼ぶ。温度による流体の密度の変化が原因となる熱対流が最も一般的な例である。
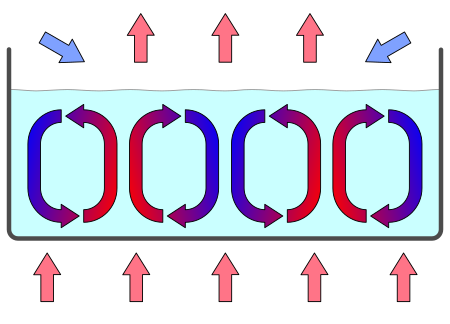
熱対流の体系的な研究は、1900年にフランスのアンリ・ベナールによる実験から始まった。パラフィン、鯨油などの粘性の高い流体層の下面を一様に加熱すると、加熱された流体は浮力により上昇するため、流体内部に半定常的な細胞状の模様(対流セル)が形成されることがある。細胞の中心付近では上昇流、境界付近では下降流になっている。これをベナール・セルと呼ぶ。1916年にレーリー卿は、その理論的な解析を行った。そのことから細胞状のパターンが生ずる熱対流をレーリー=ベナール型対流と呼ぶ。
ブジネスク近似(熱膨張による密度変化に比べて、膨張圧縮による密度変化が無視できる流体)が成り立つ流体におけるレーリー=ベナール型対流は、実際の流体の厚さには直接関係無く、レーリー数 とプラントル数 と呼ばれる無次元の物理量によってその形状が決まる。対流が発生する最小のレーリー数を臨界レーリー数と呼び、その値は(流体系の上下とも固定境界の時は)約1,708である。それを超えると順に2次元の円筒形の対流セル、3次元の規則性の対流セルへと対流が発達する。レーリー数が非常に大きくなると(流体上下の温度差が大きくなるなど)乱流に遷移し、この時定常的なセルは生じず空間スケールがより小さな不規則な流れとなる。またレーリー数が大きい場合には、流体の流れにより鉛直方向への熱の輸送量が大きくなる。
地表付近の大気などの密度成層(下層ほど密度が高くなる状態)、あるいは回転系における流体などでは、対流の程度についてそれぞれの系に合わせた別の定義がされる。雲の形成など大気中の現象では、水蒸気の凝結による潜熱の影響が現れる。惑星など中心に向けて重力場を持つ回転球体における流体では、回転軸の周囲に、平行に円筒系のセルが並ぶような対流の形状を取ることが知られている。
地球内部のマントルにおける対流により、地球表面の大規模な変動(テクトニクス)が引き起こされるプルームテクトニクス理論が提唱されている。この場合のプルームとは、対流セルによって生ずる上昇流や下降流のことを意味する。
海洋内部においても密度によって循環が生じている(熱塩循環)。ただしこの場合は塩分濃度の影響が大きいことから、対流には含まないことが多い。
水平対流
編集流体に水平方向の温度差が与えられた場合に生ずる流体の運動が水平対流である。大気においては、大陸と海洋の温度差によって生ずる季節風、海岸の近くにおける地表面と海面の温度差によって生ずる海陸風、都市部の気温が上昇すること(ヒートアイランド現象)により都心に吹き込む風が生ずる郊外風などが水平対流に分類される。
地球大気において、緯度によって太陽放射の吸収量が異なるために生ずる熱帯から極への水平対流(大気大循環)は、大きく3つに分類でき、熱帯にあるものをハドレー循環、中緯度にあるものをフェレル循環、極にあるものを極循環と呼ぶ。
マランゴニ対流
編集マランゴニ対流とは、流体表面の表面張力が不均質になることが原因で流体の流れが駆動される対流のことである。名前はイタリアの物理学者カルロ・マランゴニにちなむ。マランゴニ対流が起きると表面張力の低いほうから高いほうへ流れが生じ、周りの液体の表面張力を下げるように広がっていく。最初の表面張力の変化は主に温度差、濃度差が原因となる。ひとたびマランゴニ対流が発生すると、流れにより温度や濃度が不均質になるため、ある条件では準定常的な対流が持続する。
シリコンなどの半導体材料を溶融し、冷却して再結晶させる過程でマランゴニ対流が発生するため、均質な単結晶を生成することが難しくなることが知られている。
マランゴニ対流の解析には、次のマランゴニ数Ma という無次元量が用いられる[1]。
ここで
- σ:表面張力
- T :温度(温度差によるマランゴニ対流の場合)
- ΔT :代表温度差
- L :代表長さ
- μ:粘性
- κ:温度拡散率
である。
定常状態では表面張力σの勾配と流れが次式で関連付けられる[2]:
ここでxとzはそれぞれ水平方向と鉛直方向の座標、vxは水平方向の流速である。
強制対流
編集流体力学や伝熱工学の分野では上記の特に熱対流を自然対流や自由対流(natural convection)と呼び、ブロアやポンプ等の外部から引き起こされた強制対流(forced convection)と区別することが多い.
参考文献
編集- ^ Joel H. Ferziger; Milovan Perić 著、小林敏雄、谷口伸行、坪倉誠 訳『コンピュータによる流体力学』シュプリンガー・フェアラーク東京、2003年、378頁。ISBN 4-431-70842-1。
- ^ Hans-Jürgen Butt, Karlheinz Graf, Michael Kappl; 鈴木祥仁, 深尾浩次 共訳『界面の物理と科学』丸善出版、2016年、50頁。ISBN 978-4-621-30079-4。
関連項目
編集外部リンク
編集この節の加筆が望まれています。 |