Soubor:Hexahedron.jpg

Velikost tohoto náhledu: 538 × 599 pixelů. Jiná rozlišení: 216 × 240 pixelů | 431 × 480 pixelů | 742 × 826 pixelů.

Původní soubor (742 × 826 pixelů, velikost souboru: 51 KB, MIME typ: image/jpeg)

Tento soubor pochází z Wikimedia Commons. Níže jsou zobrazeny informace, které obsahuje jeho tamější stránka s popisem souboru.

Popis

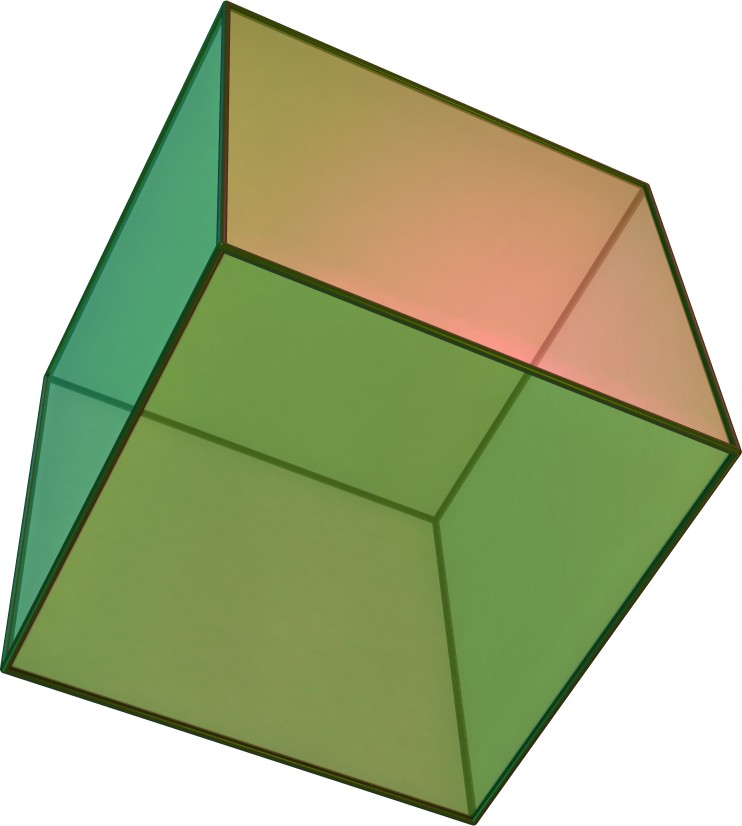
PopisHexahedron.jpg	English: A Hexahedron (cube). A regular polyhedron.
Zdroj	see below
Autor	Původně soubor načetl Cyp na projektu Wikipedie v jazyce angličtina

K tomuto obrázku existuje vektorová verze (v SVG). Pokud je lepší, používejte raději tu.

File:Hexahedron.jpg → File:Hexahedron.svg

Podrobnější informace o vektorové grafice najdete na stránce Commons:Transition to SVG.
Také si můžete přečíst informace o podpoře formátu SVG v MediaWiki.

V jiných jazycích

Alemannisch ∙ Bahasa Indonesia ∙ Bahasa Melayu ∙ British English ∙ català ∙ čeština ∙ dansk ∙ Deutsch ∙ eesti ∙ English ∙ español ∙ Esperanto ∙ euskara ∙ français ∙ Frysk ∙ galego ∙ hrvatski ∙ Ido ∙ italiano ∙ lietuvių ∙ magyar ∙ Nederlands ∙ norsk bokmål ∙ norsk nynorsk ∙ occitan ∙ Plattdüütsch ∙ polski ∙ português ∙ português do Brasil ∙ română ∙ Scots ∙ sicilianu ∙ slovenčina ∙ slovenščina ∙ suomi ∙ svenska ∙ Tiếng Việt ∙ Türkçe ∙ vèneto ∙ Ελληνικά ∙ беларуская (тарашкевіца) ∙ български ∙ македонски ∙ нохчийн ∙ русский ∙ српски / srpski ∙ татарча/tatarça ∙ українська ∙ ქართული ∙ հայերեն ∙ বাংলা ∙ தமிழ் ∙ മലയാളം ∙ ไทย ∙ 한국어 ∙ 日本語 ∙ 简体中文 ∙ 繁體中文 ∙ עברית ∙ العربية ∙ فارسی ∙ +/−

Licence

Tento dokument smí být kopírován, šířen nebo upravován podle podmínek Svobodné licence GNU pro dokumenty verze 1.2 nebo libovolné vyšší verze publikované nadací Free Software Foundation. Dokument nemá neměnné části ani texty na předním či zadním přebalu. Kopie textu licence je k dispozici v oddíle nazvaném GNU Free Documentation License.

	Tento soubor podléhá licenci Creative Commons Uveďte autora-Zachovejte licenci 3.0 Unported.

	Dílo smíte: šířit – kopírovat, distribuovat a sdělovat veřejnosti upravovat – pozměňovat, doplňovat, využívat celé nebo částečně v jiných dílech Za těchto podmínek: uveďte autora – Máte povinnost uvést autorství, poskytnout odkaz na licenci a uvést, pokud jste provedli změny. Toho můžete docílit jakýmkoli rozumným způsobem, avšak ne způsobem naznačujícím, že by poskytovatel licence schvaloval nebo podporoval vás nebo vaše užití díla. zachovejte licenci – Pokud tento materiál jakkoliv upravíte, přepracujete nebo použijete ve svém díle, musíte své příspěvky šířit pod stejnou nebo slučitelnou licencí jako originál.
	Tato licenční šablona byla k tomuto souboru přidána v rámci změny licencování.CC BY-SA 3.0truetrue

Povray src code

Hexahedron, made by me using POV-Ray, see en:User:Cyp/Poly.pov for source.}}

//Picture   ***  Use flashiness=1 !!! ***
//
//   +w1024 +h1024 +a0.3 +am2
//   +w512 +h512 +a0.3 +am2
//
//Movie   ***  Use flashiness=0.25 !!! ***
//
//   +kc +kff120 +w256 +h256 +a0.3 +am2
//   +kc +kff60 +w256 +h256 +a0.3 +am2
//"Fast" preview
//   +w128 +h128
#declare notwireframe=1;
#declare withreflection=0;
#declare flashiness=0.25; //Still pictures use 1, animated should probably be about 0.25.

#macro This_shape_will_be_drawn()
   //PLATONIC SOLIDS ***********
  //tetrahedron() #declare rotation=seed(1889/*1894*/);
  //hexahedron() #declare rotation=seed(7122);
  //octahedron() #declare rotation=seed(4193);
  //dodecahedron() #declare rotation=seed(4412);
  //icosahedron() #declare rotation=seed(7719);


  //weirdahedron() #declare rotation=seed(7412);


   //ARCHIMEDIAN SOLIDS ***********
  //cuboctahedron() #declare rotation=seed(1941);
  //icosidodecahedron() #declare rotation=seed(2241);

  //truncatedtetrahedron() #declare rotation=seed(8717);
  //truncatedhexahedron() #declare rotation=seed(1345);
  //truncatedoctahedron() #declare rotation=seed(7235);
  //truncateddodecahedron() #declare rotation=seed(9374);
  //truncatedicosahedron() #declare rotation=seed(1666);

  //rhombicuboctahedron() #declare rotation=seed(6124);
  //truncatedcuboctahedron() #declare rotation=seed(1156);
  //rhombicosidodecahedron() #declare rotation=seed(8266);
  //truncatedicosidodecahedron() #declare rotation=seed(1422);

  //snubhexahedron(-1) #declare rotation=seed(7152);
  //snubhexahedron(1) #declare rotation=seed(1477);
  //snubdodecahedron(-1) #declare rotation=seed(5111);
  //snubdodecahedron(1) #declare rotation=seed(8154);


   //CATALAN SOLIDS ***********
  //rhombicdodecahedron() #declare rotation=seed(7154);
  //rhombictriacontahedron() #declare rotation=seed(1237);

  //triakistetrahedron() #declare rotation=seed(7735);
  //triakisoctahedron() #declare rotation=seed(5354);
  //tetrakishexahedron() #declare rotation=seed(1788);
  //triakisicosahedron() #declare rotation=seed(1044);
  //pentakisdodecahedron() #declare rotation=seed(6100);

  //deltoidalicositetrahedron() #declare rotation=seed(5643);
  //disdyakisdodecahedron() #declare rotation=seed(1440);
  //deltoidalhexecontahedron() #declare rotation=seed(1026);
  //disdyakistriacontahedron() #declare rotation=seed(1556);

  //pentagonalicositetrahedron(-1) #declare rotation=seed(7771);
  //pentagonalicositetrahedron(1) #declare rotation=seed(3470);
  //pentagonalhexecontahedron(-1) #declare rotation=seed(1046);
  //pentagonalhexecontahedron(1) #declare rotation=seed(1096);

   //PRISMS, ANTIPRISMS, ETC... ***********
  //rprism(5) #declare rotation=seed(6620);
  antiprism(5) #declare rotation=seed(6620);
  //bipyramid(5) #declare rotation=seed(6620);
  //trapezohedron(17) #declare rotation=seed(6620);

#end


#declare tau=(1+sqrt(5))/2;
#declare sq2=sqrt(2);
#declare sq297=sqrt(297);
#declare xi=(pow(sq297+17,1/3)-pow(sq297-17,1/3)-1)/3;
#declare sqweird=sqrt(tau-5/27);
#declare ouch=pow((tau+sqweird)/2,1/3)+pow((tau-sqweird)/2,1/3);
#declare alfa=ouch-1/ouch;
#declare veta=(ouch+tau+1/ouch)*tau;

#macro tetrahedron()
  addpointsevensgn(<1,1,1>)
  autoface()
#end

#macro hexahedron()
  addpointssgn(<1,1,1>,<1,1,1>)
  autoface()
#end

#macro octahedron()
  addevenpermssgn(<1,0,0>,<1,0,0>)
  autoface()
#end

#macro dodecahedron()
  addpointssgn(<1,1,1>,<1,1,1>)
  addevenpermssgn(<0,1/tau,tau>,<0,1,1>)
  autoface()
#end

#macro icosahedron()
  addevenpermssgn(<0,1,tau>,<0,1,1>)
  autoface()
#end


#macro weirdahedron()
  addpermssgn(<1,2,3>,<1,1,1>)
  autoface()
#end


#macro cuboctahedron()
  addevenpermssgn(<0,1,1>,<0,1,1>)
  autoface()
#end

#macro icosidodecahedron()
  addevenpermssgn(<0,0,2*tau>,<0,0,1>)
  addevenpermssgn(<1,tau,1+tau>,<1,1,1>)
  autoface()
#end


#macro truncatedtetrahedron()
  addevenpermsevensgn(<1,1,3>)
  autoface()
#end

#macro truncatedhexahedron()
  addevenpermssgn(<sq2-1,1,1>,<1,1,1>)
  autoface()
#end

#macro truncatedoctahedron()
  addpermssgn(<0,1,2>,<0,1,1>)
  autoface()
#end

#macro truncateddodecahedron()
  addevenpermssgn(<0,1/tau,2+tau>,<0,1,1>)
  addevenpermssgn(<1/tau,tau,2*tau>,<1,1,1>)
  addevenpermssgn(<tau,2,1+tau>,<1,1,1>)
  autoface()
#end

#macro truncatedicosahedron()
  addevenpermssgn(<0,1,3*tau>,<0,1,1>)
  addevenpermssgn(<2,1+2*tau,tau>,<1,1,1>)
  addevenpermssgn(<1,2+tau,2*tau>,<1,1,1>)
  autoface()
#end


#macro rhombicuboctahedron()
  addevenpermssgn(<1+sq2,1,1>,<1,1,1>)
  autoface()
#end

#macro truncatedcuboctahedron()
  addpermssgn(<1,1+sq2,1+sq2*2>,<1,1,1>)
  autoface()
#end

#macro rhombicosidodecahedron()
  addevenpermssgn(<1,1,1+2*tau>,<1,1,1>)
  addevenpermssgn(<tau,2*tau,1+tau>,<1,1,1>)
  addevenpermssgn(<2+tau,0,1+tau>,<1,0,1>)
  autoface()
#end

#macro truncatedicosidodecahedron()
  addevenpermssgn(<1/tau,1/tau,3+tau>,<1,1,1>)
  addevenpermssgn(<2/tau,tau,1+2*tau>,<1,1,1>)
  addevenpermssgn(<1/tau,1+tau,3*tau-1>,<1,1,1>)
  addevenpermssgn(<2*tau-1,2,2+tau>,<1,1,1>)
  addevenpermssgn(<tau,3,2*tau>,<1,1,1>)
  autoface()
#end


#macro snubhexahedron(s)
  addpermsaltsgn(<1,1/xi,xi>*s)
  autoface()
#end

#macro snubdodecahedron(s)
  addevenpermsevensgn(<2*alfa,2,2*veta>*s)
  addevenpermsevensgn(<alfa+veta/tau+tau,-alfa*tau+veta+1/tau,alfa/tau+veta*tau-1>*s)
  addevenpermsevensgn(<-alfa/tau+veta*tau+1,-alfa+veta/tau-tau,alfa*tau+veta-1/tau>*s)
  addevenpermsevensgn(<-alfa/tau+veta*tau-1,alfa-veta/tau-tau,alfa*tau+veta+1/tau>*s)
  addevenpermsevensgn(<alfa+veta/tau-tau,alfa*tau-veta+1/tau,alfa/tau+veta*tau+1>*s)
  autoface()
#end

#macro rhombicdodecahedron()
  cuboctahedron() dual()
#end

#macro rhombictriacontahedron()
  icosidodecahedron() dual()
#end

#macro triakistetrahedron()
  truncatedtetrahedron() dual()
#end

#macro triakisoctahedron()
  truncatedhexahedron() dual()
#end

#macro tetrakishexahedron()
  truncatedoctahedron() dual()
#end

#macro triakisicosahedron()
  truncateddodecahedron() dual()
#end

#macro pentakisdodecahedron()
  truncatedicosahedron() dual()
#end

#macro deltoidalicositetrahedron()
  rhombicuboctahedron() dual()
#end

#macro disdyakisdodecahedron()
  truncatedcuboctahedron() dual()
#end

#macro deltoidalhexecontahedron()
  rhombicosidodecahedron() dual()
#end

#macro disdyakistriacontahedron()
  truncatedicosidodecahedron() dual()
#end

#macro pentagonalicositetrahedron(s)
  snubhexahedron(s) dual()
#end

#macro pentagonalhexecontahedron(s)
  snubdodecahedron(s) dual()
#end

#macro rprism(n)
  #local a=sqrt((1-cos(2*pi/n))/2);
  #local b=0; #while(b<n-.5)
    addpointssgn(<sin(2*pi*b/n),cos(2*pi*b/n),a>,<0,0,1>)
  #local b=b+1; #end
  autoface()
#end

#macro antiprism(n)
  #local a=sqrt((cos(pi/n)-cos(2*pi/n))/2);
  #local b=0; #while(b<2*n-.5)
    addpoint(<sin(pi*b/n),cos(pi*b/n),a>)
  #local a=-a; #local b=b+1; #end
  autoface()
#end

#macro bipyramid(n)
  rprism(n) dual()
#end

#macro trapezohedron(n)
  antiprism(n) dual()
#end


#declare points=array[1000];
#declare npoints=0;
#declare faces=array[1000];
#declare nfaces=0;
#macro addpoint(a)
  #declare points[npoints]=a;
  #declare npoints=npoints+1;
#end
#macro addevenperms(a)
  addpoint(a)
  addpoint(<a.y,a.z,a.x>)
  addpoint(<a.z,a.x,a.y>)
#end
#macro addperms(a)
  addevenperms(a)
  addevenperms(<a.x,a.z,a.y>)
#end
#macro addpointssgn(a,s)
  addpoint(a)
  #if(s.x) addpointssgn(a*<-1,1,1>,s*<0,1,1>) #end
  #if(s.y) addpointssgn(a*<1,-1,1>,s*<0,0,1>) #end
  #if(s.z) addpoint(a*<1,1,-1>) #end
#end
#macro addevenpermssgn(a,s)
  addpointssgn(a,s)
  addpointssgn(<a.y,a.z,a.x>,<s.y,s.z,s.x>)
  addpointssgn(<a.z,a.x,a.y>,<s.z,s.x,s.y>)
#end
#macro addpermssgn(a,s)
  addevenpermssgn(a,s)
  addevenpermssgn(<a.x,a.z,a.y>,<s.x,s.z,s.y>)
#end
#macro addpointsevensgn(a)
  addpoint(a)
  addpoint(a*<-1,-1,1>)
  addpoint(a*<-1,1,-1>)
  addpoint(a*<1,-1,-1>)
#end
#macro addevenpermsevensgn(a)
  addevenperms(a)
  addevenperms(a*<-1,-1,1>)
  addevenperms(a*<-1,1,-1>)
  addevenperms(a*<1,-1,-1>)
#end
#macro addpermsaltsgn(a)
  addevenpermsevensgn(a)
  addevenpermsevensgn(<a.x,a.z,-a.y>)
#end
/*#macro addevenpermssgn(a,s) //Calls addevenperms with, for each 1 in s, a.{x,y,z} replaced with {+,-}a.{x,y,z}
  addevenperms(a)
  #if(s.x) addevenpermssgn(a*<-1,1,1>,s*<0,1,1>) #end
  #if(s.y) addevenpermssgn(a*<1,-1,1>,s*<0,0,1>) #end
  #if(s.z) addevenperms(a*<1,1,-1>) #end
#end*/
#macro addface(d,l)
  #local a=vnormalize(d)/l; 
  #local f=1;
  #local n=0; #while(n<nfaces-.5)
    #if(vlength(faces[n]-a)<0.00001) #local f=0; #end
  #local n=n+1; #end
  #if(f)
    #declare faces[nfaces]=a;
    #declare nfaces=nfaces+1;
  #end
#end
#macro dual()
  #declare temp=faces;
  #declare faces=points;
  #declare points=temp; 
  #declare temp=nfaces;
  #declare nfaces=npoints;
  #declare npoints=temp; 
#end

#macro autoface() //WARNING: ONLY WORKS IF ALL EDGES HAVE EQUAL LENGTH
  //Find edge length 
  #declare elength=1000;
  #local a=0; #while(a<npoints-.5) #local b=0; #while(b<npoints-.5)
    #local c=vlength(points[a]-points[b]); #if(c>0.00001 & c<elength) #local elength=c; #end
  #local b=b+1; #end #local a=a+1; #end

  //Find planes
  //#macro planes()
  #local a=0; #while(a<npoints-.5)
    #local b=a+1; #while(b<npoints-.5)
      #if(vlength(points[a]-points[b])<elength+0.00001) #local c=b+1; #while(c<npoints-.5)
        #if(vlength(points[a]-points[c])<elength+0.00001)
          #local n=vnormalize(vcross(points[b]-points[a],points[c]-points[a]));
          #local d=vdot(n,points[a]);
          #if(d<0) #local n=-n; #local d=-d; #end
          #local f=1;
          #local e=0; #while(e<npoints-.5)
            #if(vdot(n, points[e])>d+0.00001) #local f=0; #end
          #local e=e+1; #end
          #if(f)
            #declare ld=d;
            addface(n,d) //plane { n, d }
          #end
        #end
      #local c=c+1; #end #end
    #local b=b+1; #end
  #local a=a+1; #end
#end

This_shape_will_be_drawn()

//Random rotations are (hopefully) equally distributed...
#declare rot1=rand(rotation)*pi*2;
#declare rot2=acos(1-2*rand(rotation));
#declare rot3=(rand(rotation)+clock)*pi*2;
#macro dorot()
  rotate rot1*180/pi*y
  rotate rot2*180/pi*x
  rotate rot3*180/pi*y
#end

//Scale shape to fit in unit sphere
#local b=0;
#local a=0; #while(a<npoints-.5)
  #local c=vlength(points[a]); #if(c>b) #local b=c; #end
#local a=a+1; #end
#local a=0; #while(a<npoints-.5)
  #local points[a]=points[a]/b;
#local a=a+1; #end
#local a=0; #while(a<nfaces-.5)
  #local faces[a]=faces[a]*b;
#local a=a+1; #end

//Draw edges
#macro addp(a)
  #declare p[np]=a;
  #declare np=np+1;
#end
#local a=0; #while(a<nfaces-.5)
  #declare p=array[20];
  #declare np=0;
  #local b=0; #while(b<npoints-.5)
    #if(vdot(faces[a],points[b])>1-0.00001) addp(b) #end
  #local b=b+1; #end
  #local c=0; #while(c<np-.5)
    #local d=0; #while(d<np-.5) #if(p[c]<p[d]-.5)
      #local f=1;
      #local e=0; #while(e<np-.5) #if(e!=c & e!=d & vdot(vcross(points[p[c]],points[p[d]]),points[p[e]])<0)
        #local f=0;
      #end #local e=e+1; #end
      #if(f)
        object {
          cylinder { points[p[c]], points[p[d]], .01 dorot() }
          pigment { colour <.3,.3,.3> }
          finish { ambient 0 diffuse 1 phong 1 }
        }
      #end #end        
    #local d=d+1; #end
  #local c=c+1; #end
#local a=a+1; #end
/*#local a=0; #while(a<npoints-.5)
  #local b=a+1; #while(b<npoints-.5)
    #if(vlength(points[a]-points[b])<elength+0.00001)
      object {
        cylinder { points[a], points[b], .01 dorot() }
        pigment { colour <.3,.3,.3> }
        finish { ambient 0 diffuse 1 phong 1 }
      }
    #end
  #local b=b+1; #end
#local a=a+1; #end*/

//Draw points
#local a=0; #while(a<npoints-.5)
  object {
    sphere { points[a], .01 dorot() }
    pigment { colour <.3,.3,.3> }
    finish { ambient 0 diffuse 1 phong 1 }
  }
#local a=a+1; #end

#if(notwireframe)
//Draw planes
object {
  intersection {
    #local a=0; #while(a<nfaces-.5)
      plane { faces[a], 1/vlength(faces[a]) }
    #local a=a+1; #end
    //planes()
    //sphere { <0,0,0>, 1 }
    //sphere { <0,0,0>, ld+.01 inverse }
    dorot()
  }
  pigment { colour rgbt <.8,.8,.8,.4> }
  finish { ambient 0 diffuse 1 phong flashiness #if(withreflection) reflection { .2 } #end }
  //interior { ior 1.5 }
  photons {
    target on
    refraction on
    reflection on
    collect on
  }
}
#end

//  CCC Y Y PP
//  C   Y Y P P
//  C    Y  PP
//  C    Y  P
//  CCC  Y  P

#local a=0;
#while(a<11.0001)
  light_source { <4*sin(a*pi*2/11), 5*cos(a*pi*6/11), -4*cos(a*pi*2/11)> colour (1+<sin(a*pi*2/11),sin(a*pi*2/11+pi*2/3),sin(a*pi*2/11+pi*4/3)>)*2/11 }
  #local a=a+1;
#end

background { color <1,1,1> }

camera {
  perspective
  location <0,0,0>
  direction <0,0,1>
  right x/2
  up y/2
  sky <0,1,0>
  location <0,0,-4.8>
  look_at <0,0,0>
}

global_settings {
  max_trace_level 40
  photons {
    count 200000
    autostop 0
  }
}

K tomuto obrázku existuje vektorová verze (v SVG). Měla by být použita místo tohoto rastrového obrázku.

File:Hexahedron.jpg → File:Hexahedron.svg

Podrobnější informace o vektorové grafice najdete na stránce Commons:Transition to SVG.
Také si můžete přečíst informace o podpoře formátu SVG v MediaWiki.

V jiných jazycích