M.Saadatmanesh, R.E.Kennedy, and C.Cooper defined and studied
the super Niven numbers (sN for brevity).
A number is called sN if it is divisible not only by the sum of its digits (like Harshad numbers) but also by the sum of any subset of its (nonzero) digits.
For example, the number 68040 is sN because it is divisible by 6, 8, 4, 6+8, 6+4, 4+8 and 6+4+8.
If is sN, then clearly also
is sN.
The primitive
sN numbers are those such that
is not sN.
It is easy to see that there are infinite primitive sN, because
all the numbers of the form are sN, being divisible
by 1, 2, and 1 + 2 = 3.
The first super Niven numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 20, 24, 30, 36, 40, 48, 50, 60, 70, 80, 90, 100, 102, 110, 120, 140, 150, 200, 204, 210, 220, 240, 280, 300, 306, 330, 360, 400, 408, 420, 440, 480, 500 more terms
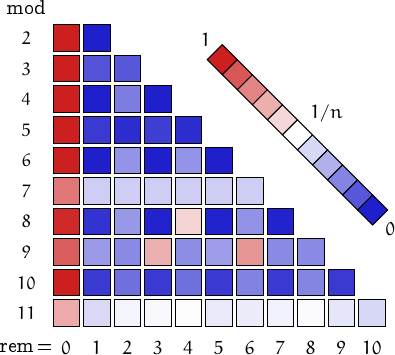
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
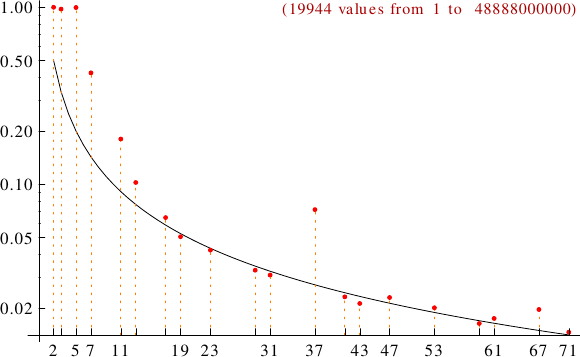
A graph displaying how many super Niven numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.
Useful links
M.Saadatmanesh, R.E.Kennedy, C.Cooper, Super Niven numbers
Super Niven numbers can also be... (you may click on names or numbers and on + to get more values)
ABA
24
50
200
+
45000000000
aban
10
12
20
+
48888000000
abundant
12
20
24
+
50000000
Achilles
200
500
800
+
45000000000
admirable
12
20
24
+
1000002
alternating
10
12
30
+
909090
amenable
12
20
24
+
1000000000
amicable
220
apocalyptic
220
540
660
+
30000
arithmetic
20
30
60
+
9909000
astonishing
204
betrothed
48
140
1050
binomial
10
20
36
+
20000100000
brilliant
10
c.nonagonal
10
2080
5050
+
5000050000
c.triangular
10
compositorial
24
congruent
20
24
30
+
9990000
constructible
10
12
20
+
4080
cube
1000
8000
1000000
+
8000000000
Cunningham
10
24
48
+
48400440000
Curzon
30
50
90
+
101000010
d-powerful
24
8200
42240
262200
decagonal
10
540
4000
69300
deficient
10
50
110
+
1000010
dig.balanced
10
12
50
+
180000000
double fact.
48
droll
240
800
Duffinian
36
50
100
+
9000000
eban
30
36
40
+
46006002000
economical
10
1000
2000
+
20000000
equidigital
10
1000
2000
+
15300000
eRAP
20
24
20220
esthetic
10
12
210
+
101010
Eulerian
120
evil
10
12
20
+
999099900
factorial
24
120
5040
40320
Friedman
12600
126000
153000
282240
frugal
10000
20000
40000
+
999000000
gapful
100
110
120
+
48888000000
Gilda
110
220
330
+
990
Giuga
30
happy
10
70
100
+
10000000
harmonic
140
30240
360360
Harshad
10
12
20
+
10000000000
heptagonal
540
351000
hexagonal
120
630
2016
+
2031120
highly composite
12
24
36
+
2205403200
hoax
660
2640
6060
+
96300000
iban
10
12
20
+
777000
idoneal
10
12
24
+
1320
inconsummate
630
840
2016
+
936000
interprime
12
30
50
+
99900000
Jordan-Polya
12
24
36
+
604800
junction
204
210
408
+
93000060
Kaprekar
5050
500500
50005000
5000050000
katadrome
10
20
30
+
840
Leyland
100
20000000000
lonely
120
Lynch-Bell
12
24
36
48
magic
500050
4000100
500000500
4000001000
magnanimous
12
20
30
+
110
metadrome
12
24
36
48
modest
100110
101010
200220
+
1400200200
nialpdrome
10
20
30
+
44444400000
nonagonal
24
204
4200
+
30060063000
nude
12
24
36
48
O'Halloran
12
20
36
+
660
oban
10
12
20
+
990
octagonal
40
280
408
+
606600
odious
50
70
100
+
1000000000
panconsummate
10
12
20
+
40
pandigital
120
210
990
+
360033300
partition
30
1002
pentagonal
12
70
210
+
8400
pernicious
10
12
20
+
9903600
Perrin
10
12
90
plaindrome
12
24
36
48
power
36
100
400
+
44100000000
powerful
36
100
200
+
45000000000
practical
12
20
24
+
10000000
prim.abundant
12
20
30
+
1000002
primorial
30
210
30030
pronic
12
20
30
+
40000200000
pseudoperfect
12
20
24
+
1000000
repunit
40
400
Ruth-Aaron
24
50
2020800
848000400
Saint-Exupery
60
480
2040
+
40260000000
self
20
110
400
+
888880800
semiprime
10
sliding
20
70
110
+
20000050000
sphenic
30
70
102
+
1000002
square
36
100
400
+
44100000000
straight-line
210
420
630
840
super-d
1050
3330
10500
+
9300060
superabundant
12
24
36
+
1102701600
tau
12
24
36
+
1000000000
taxicab
513000
4104000
111321000
+
4104000000
tetrahedral
10
20
120
+
7207200
triangular
10
36
120
+
20000100000
tribonacci
24
trimorphic
24
uban
10
12
20
+
48048000000
Ulam
36
48
102
+
9306000
undulating
1010
2020
3030
+
909090
unprimeable
200
204
510
+
10000000
untouchable
120
210
306
+
999000
vampire
15003000
1050021000
1500030000
wasteful
12
20
24
+
9990000
weird
70
Woodall
80
Zuckerman
12
24
36
Zumkeller
12
20
24
+
100000
zygodrome
1100
2200
3300
+
44880000000