[go: up one dir, main page]
Search a number
house numbers
The  $n$-th house number  $h_n$  is a figurate number made by a cube of side  $n+1$, surmounted by a square pyramidal number with side  $n$, thus  $h_n = (n+1)^3 + \sum_{k=1}^nk^2$  or
\[h_n=(8 n^3+21 n^2+19 n+6)/6.\]

It holds  $\sum_{k=0}^{\infty}{h_k/2^k} = 64$.

The first house numbers are 1, 9, 32, 78, 155, 271, 434, 652, 933, 1285, 1716, 2234, 2847, 3563, 4390, 5336, 6409, 7617, 8968 more terms

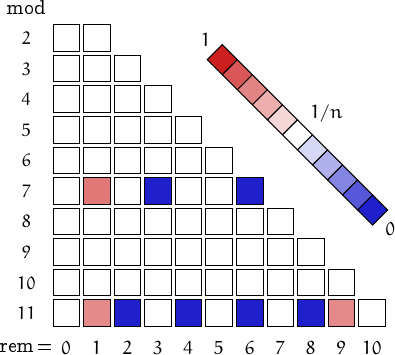
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
remainders of house numbers

A graph displaying how many house numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.
divisibility of house numbers
Useful links OEIS, Sequence A051662
House numbers can also be... (you may click on names or numbers and on + to get more values)

ABA 32 aban 32 78 155 271 434 + 496395000893 561123000943 abundant 78 1716 5336 8968 10470 + 45297198 46996332 admirable 78 6308092 alternating 32 78 434 652 32103 + 30501458 50521016 amenable 32 652 933 1285 1716 + 991159621 994445684 apocalyptic 434 1285 2234 2847 4390 + 25884 28882 arithmetic 78 155 271 434 933 + 9716393 9867520 binomial 78 1716 7759830 c.square 1582421 congruent 78 271 434 933 1285 + 8983863 9272286 constructible 32 1285 Curzon 78 933 20525 78338 91061 + 195012134 197241353 cyclic 271 933 1285 3563 6409 + 9127315 9716393 D-number 933 7617 d-powerful 874234 2596375 9272286 de Polignac 12131 165425 197107 245309 516037 + 80854117 81473093 deficient 32 155 271 434 652 + 9566817 9716393 dig.balanced 78 434 652 2234 10470 + 188425381 189512709 Duffinian 32 155 1285 2847 3563 + 8562541 9716393 eban 32 economical 32 155 271 1285 3563 + 12862147 16838677 emirpimes 155 933 2234 3563 7617 + 76608841 99402731 equidigital 32 155 271 1285 3563 + 12862147 16838677 esthetic 32 78 434 evil 78 652 933 1285 1716 + 994445684 997739002 Friedman 1285 frugal 1175056 178825984 gapful 10470 20525 120495 232596 559700 + 97370773830 97790688541 Gilda 78 happy 32 1285 2847 3563 5336 + 7130550 9418784 Harshad 13959 15962 32103 220330 315859 + 9960834480 9991438059 hex 271 hexagonal 7759830 hoax 18148 165425 258477 12862147 19102392 + 65840534 83980587 iban 271 10470 23101 47377 72447 idoneal 78 impolite 32 inconsummate 933 1716 5336 25884 32103 + 605759 654278 interprime 933 2847 6409 10470 12131 + 92484316 95211790 Jordan-Polya 32 junction 1716 7617 112618 516037 705321 + 93161234 99402731 katadrome 32 652 Lehmer 1285 Leyland 32 lucky 933 1285 23101 197107 516037 + 5551441 9566817 magnanimous 32 metadrome 78 modest 933 3563 35555 220330 8289108 Moran 6308092 7008923 15777182 27994726 nialpdrome 32 652 933 nonagonal 319118031 nude 155 1288848 13413636 oban 78 933 odious 32 155 271 434 3563 + 965131337 984609228 palindromic 434 28882 339585933 panconsummate 78 271 pandigital 78 13600909 pernicious 155 271 434 4390 6409 + 9127315 9867520 plaindrome 78 155 2234 35555 power 32 1175056 powerful 32 1175056 practical 32 78 1716 56560 232596 + 9272286 9867520 prim.abundant 78 5336 8968 6308092 prime 271 pseudoperfect 78 1716 5336 8968 10470 + 679480 758952 Ruth-Aaron 78 253313950 self 28882 35555 78338 105092 137334 + 930092234 965131337 semiprime 155 933 1285 2234 3563 + 76608841 99402731 Smith 25884 56560 258477 582426 12862147 + 75423808 83980587 sphenic 78 434 2847 4390 6409 + 93841447 96595409 square 1175056 strobogrammatic 8968 super-d 12131 66859 78338 105092 128731 + 8289108 9566817 tau 25884 56560 146312 495084 5448560 + 603684992 958696256 triangular 78 7759830 twin 271 uban 32 78 Ulam 155 434 4390 15962 47377 + 6536245 8841922 undulating 434 unprimeable 1716 15962 28882 35555 78338 + 9272286 9418784 untouchable 1716 25884 56560 78338 84540 + 679480 758952 wasteful 78 434 652 933 1716 + 9716393 9867520 weak prime 271 Zumkeller 78 1716 5336 8968 10470 + 61566 84540