A number is called bemirp (short for bi-directional emirp) if it yields a different prime when turned upside down with reversals of both being two more different primes.
For example, 168601 produces 106861, 198901 and 109891.
The only digits allowed in a bemirp are 0, 1, 6, 8 and 9.
Every number greater than 40258 can be written as the sum of bemirps.
The first bemirps are 1061, 1091, 1601, 1901, 10061, 10091, 16001, 19001, 106861, 109891, 168601, 198901, 1106881, 1109881 more terms
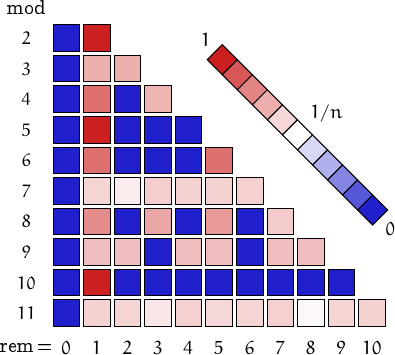
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
Bemirps can also be... (you may click on names or numbers and on + to get more values)
a-pointer
198901
18991981
110098601
1016910161
1069110901
1161110191
1166019611
1190010161
1191110161
1601169611
aban
10601000101
10901000101
11060000101
11090000101
16160000161
19190000191
106068000611
106080000011
106690000661
106989000191
+
189908000011
190608000911
196169000081
199889000881
alternating
109698961
169896901
amenable
1061
1601
1901
10061
16001
19001
106861
168601
198901
1106881
+
199089061
199109681
199180081
199680881
apocalyptic
10061
10091
16001
19001
arithmetic
1061
1091
1601
1901
10061
10091
16001
19001
106861
109891
+
1809091
1886011
1889011
1909081
balanced p.
18616681
168910801
199109681
1088900611
1161111661
1180606991
1198600801
1610889101
1666116901
1690896061
1969081091
c.decagonal
1901
199068088111
c.pentagonal
119010099181
Chen
1061
1091
1601
1901
10061
10091
16001
19001
198901
1109881
+
19091981
19199981
19689611
19880981
congruent
1061
1901
10061
106861
198901
1806061
Cunningham
1601
Curzon
1601
1901
10061
16001
11906981
16880681
18890801
106891601
109168901
110600981
199680881
cyclic
1061
1091
1601
1901
10061
10091
16001
19001
106861
109891
+
1809091
1886011
1889011
1909081
de Polignac
10061
16061681
16880681
18690611
18908891
18999191
deficient
1061
1091
1601
1901
10061
10091
16001
19001
106861
109891
+
1809091
1886011
1889011
1909081
dig.balanced
16001
198901
11816011
161188681
161899861
168668881
168910801
186009011
188089661
189166801
economical
1061
1091
1601
1901
10061
10091
16001
19001
106861
109891
+
19199981
19689611
19880981
19986091
emirp
1061
1091
1601
1901
10061
10091
16001
19001
106861
109891
+
199180081
199198891
199680881
199800091
equidigital
1061
1091
1601
1901
10061
10091
16001
19001
106861
109891
+
19199981
19689611
19880981
19986091
evil
1061
1091
1601
1901
10061
168601
1806061
1809091
1909081
11091811
+
196899191
198816811
198888601
199800091
good prime
10061
10091
19001
happy
1106881
1886011
Honaker
1091
1606081
1806061
106891601
109168901
118880911
161080811
169806181
inconsummate
1601
16001
lucky
1606081
odious
10091
16001
19001
106861
109891
198901
1106881
1109881
1606081
1886011
+
199109681
199180081
199198891
199680881
Ormiston
1969081091
pernicious
16001
19001
1109881
1606081
1886011
1889011
prime
1061
1091
1601
1901
10061
10091
16001
19001
106861
109891
+
199996091101
199996180081
199998990101
199999069901
Proth
1601
16001
self
16001
198901
11816011
16098661
16689061
18616681
18661681
106186681
110600981
110900681
+
190680661
198969611
199180081
199800091
Sophie Germain
1601
1901
10061
10091
16001
11906981
16880681
18890801
106891601
109168901
+
1961009111
1981868081
1986199601
1988809001
strong prime
1061
1091
1901
10061
10091
16001
19001
109891
1106881
1109881
+
18919091
18960911
19068991
19091981
super-d
1061
1901
19001
106861
1106881
1109881
1606081
1806061
1909081
twin
1061
1091
10091
106861
168601
198901
1806061
1889011
1909081
11816011
+
198668191
198969611
198998881
199680881
uban
1088016000011
1088019000011
16068066000061
19098099000091
Ulam
168601
1606081
weak prime
1601
106861
168601
198901
1806061
1889011
1909081
10806881
11061811
11609681
+
19199981
19689611
19880981
19986091