A number  is said to be amenable if there exist
is said to be amenable if there exist  numbers
numbers
 in
in  such that
such that 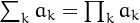 , i.e., their sum is equal to their product.
, i.e., their sum is equal to their product.
For example, 8 is amenable because the 8 numbers {-1, -1, 1, 1, 1, 1, 2, 4} have the same sum and product.
O. P. Lossers proved that is amenable
if and only if
and it is of the form
or
.
The first amenable numbers are 1, 5, 8, 9, 12, 13, 16, 17, 20, 21, 24, 25, 28, 29, 32, 33 more terms
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

A graph displaying how many amenable numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Amenable numbers can also be... (you may click on names or numbers and on + to get more values)
a-pointer
13
101
181
+
999968341
ABA
24
32
64
+
999939200
aban
12
13
16
+
1000000000
abundant
12
20
24
+
50000000
Achilles
72
108
200
+
999939200
admirable
12
20
24
+
99999956
alt.fact.
101
4421
326981
36614981
alternating
12
16
21
+
989898989
amicable
220
284
1184
+
999728396
anti-perfect
244
285
133857
141635817
apocalyptic
157
192
220
+
30000
arithmetic
13
17
20
+
9999997
astonishing
204
216
429
+
793039833
automorphic
25
76
376
+
787109376
balanced p.
53
157
173
+
999998789
Bell
52
877
4140
+
27644437
bemirp
1061
1601
1901
+
199680881
betrothed
48
140
1648
+
991087064
binomial
20
21
28
+
999961560
brilliant
21
25
49
+
999999421
c.decagonal
61
101
281
+
999768701
c.heptagonal
148
197
253
+
999930772
c.nonagonal
28
136
253
+
999916840
c.octagonal
25
49
81
+
999887641
c.pentagonal
16
76
141
+
999950001
c.square
13
25
41
+
999983921
c.triangular
64
85
109
+
999814960
cake
64
93
176
+
998152597
Canada
125
581
8549
Carmichael
561
1105
1729
+
993905641
Catalan
132
429
16796
+
477638700
Chen
13
17
29
+
99999721
compositorial
24
192
1728
+
696729600
congruent
13
20
21
+
9999997
constructible
12
16
17
+
858980352
cube
64
125
216
+
1000000000
Cullen
25
65
161
+
838860801
Cunningham
17
24
28
+
999950885
Curzon
21
29
33
+
199999973
cyclic
13
17
29
+
9999997
D-number
21
33
57
+
7043133
d-powerful
24
89
132
+
9999865
de Polignac
149
337
373
+
99999937
decagonal
52
85
232
+
999650497
deceptive
481
1729
2821
+
999888709
deficient
13
16
17
+
9999997
dig.balanced
12
21
37
+
199999936
double fact.
48
105
384
+
185794560
droll
72
240
672
+
995328000
Duffinian
16
21
25
+
9999997
eban
32
36
40
+
66066064
economical
13
16
17
+
20000000
emirp
13
17
37
+
199999777
emirpimes
49
85
93
+
99999997
enlightened
256
2048
2176
+
761743661
equidigital
13
16
17
+
19999985
eRAP
20
24
1104
+
999393125
esthetic
12
21
32
+
989898989
Eulerian
57
120
1013
+
848090912
evil
12
17
20
+
999999997
factorial
24
120
720
+
479001600
fibodiv
28
61
149
+
984380344
Fibonacci
13
21
89
+
701408733
Friedman
25
121
125
+
999964
frugal
125
128
256
+
999999189
gapful
100
105
108
+
1000000000
Gilda
29
49
152
+
92078232
good prime
17
29
37
+
199968469
happy
13
28
32
+
10000000
harmonic
28
140
496
+
995248800
Harshad
12
20
21
+
1000000000
heptagonal
81
112
148
+
999970000
hex
37
61
169
+
999899377
hexagonal
28
45
120
+
999916840
highly composite
12
24
36
+
735134400
hoax
84
85
136
+
99999332
Hogben
13
21
57
+
999856021
Honaker
457
1049
1301
+
999843421
house
32
652
933
+
994445684
hungry
17
144
37929
+
33662541
hyperperfect
21
28
301
+
974380921
iban
12
17
20
+
777777
iccanobiF
13
124
836
+
265429972
idoneal
12
13
16
+
1848
impolite
16
32
64
+
536870912
inconsummate
65
84
161
+
999993
insolite
11112
1122112
122121216
interprime
12
21
45
+
99999980
Jacobsthal
21
85
341
+
357913941
Jordan-Polya
12
16
24
+
995328000
junction
101
105
109
+
99999968
Kaprekar
45
297
2728
+
909090909
katadrome
20
21
32
+
987654321
Lehmer
85
133
481
+
999962185
Leyland
17
32
57
+
536871753
lonely
53
120
1340
+
325737821
Lucas
29
76
521
+
969323029
lucky
13
21
25
+
9999997
Lynch-Bell
12
24
36
+
9867312
m-pointer
61
1321
11261
+
211121213
magic
65
260
369
+
995433385
magnanimous
12
16
20
+
995955112
metadrome
12
13
16
+
123456789
modest
13
29
49
+
999998001
Moran
21
45
84
+
99999965
Motzkin
21
2188
310572
18199284
narcissistic
153
8208
54748
+
912985153
nialpdrome
20
21
32
+
1000000000
nonagonal
24
204
261
+
999474456
nude
12
24
33
+
499999968
O'Halloran
12
20
36
+
924
oban
12
13
16
+
997
octagonal
21
40
65
+
999917633
odious
13
16
21
+
1000000000
Ormiston
1913
18397
19013
+
999999113
palindromic
33
44
77
+
989999989
palprime
101
181
313
+
989969989
pancake
16
29
37
+
999961561
panconsummate
12
20
21
+
3097
pandigital
21
108
120
+
381367044
partition
56
77
101
+
952050665
pentagonal
12
92
117
+
999918232
perfect
28
496
8128
33550336
pernicious
12
13
17
+
9999997
Perrin
12
17
29
+
468557684
Pierpont
13
17
37
+
725594113
plaindrome
12
13
16
+
888888889
Poulet
341
561
645
+
998724481
power
16
25
32
+
1000000000
powerful
16
25
32
+
1000000000
practical
12
16
20
+
10000000
prim.abundant
12
20
56
+
99999956
prime
13
17
29
+
999999937
primeval
13
37
113
+
100123469
pronic
12
20
56
+
999856020
Proth
13
17
25
+
999981057
pseudoperfect
12
20
24
+
33550336
rare
65
repdigit
33
44
77
+
888888888
repfigit
28
61
197
+
251133297
repunit
13
21
40
+
999856021
Rhonda
1568
4752
5265
+
983314513
Ruth-Aaron
16
24
25
+
999857817
Saint-Exupery
60
480
780
+
997350120
Sastry
328
528
13224
+
897506928
self
20
53
64
+
999999972
self-describing
4444
224444
442244
+
88888888
semiprime
21
25
33
+
99999997
sliding
20
25
29
+
986802500
Smith
85
121
265
+
99999920
Sophie Germain
29
41
53
+
999998801
sphenic
105
165
273
+
99999969
square
16
25
36
+
999950884
star
13
37
73
+
999931141
straight-line
321
333
345
+
987654321
strobogrammatic
69
88
96
+
969986696
strong prime
17
29
37
+
99999821
subfactorial
44
265
14833
+
176214841
super Niven
12
20
24
+
1000000000
super-d
69
81
105
+
9999981
superabundant
12
24
36
+
735134400
tau
12
24
36
+
1000000000
taxicab
1729
4104
13832
+
998951616
tetrahedral
20
56
84
+
999800616
tetranacci
29
56
108
+
387559437
triangular
21
28
36
+
999961560
tribonacci
13
24
44
+
334745777
trimorphic
24
25
49
+
925781249
truncatable prime
13
17
29
+
999818353
twin
13
17
29
+
999999193
uban
12
13
16
+
1000000000
Ulam
13
16
28
+
10000241
undulating
101
121
141
+
989898989
unprimeable
200
204
208
+
10000000
untouchable
52
88
96
+
999996
upside-down
28
37
64
+
989951121
vampire
1260
6880
104260
+
96977920
wasteful
12
20
24
+
9999997
weak prime
13
61
73
+
99999941
weakly prime
294001
584141
1282529
+
998740213
weird
836
7192
7912
+
997348
Wieferich
1093
10533
14209
+
748316985
Woodall
17
80
4373
+
215233604
Zeisel
105
1729
1885
+
995762585
Zuckerman
12
24
36
+
997711344
Zumkeller
12
20
24
+
100000
zygodrome
33
44
77
+
999999988