A de Polignac number is an odd number 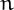 that cannot
be expressed as
that cannot
be expressed as  , for
, for  prime.
prime.
The name comes from the fact that de Polignac erroneously conjectured that every odd number can be expressed in that way.
Erdös proved that there are infinite such numbers, for example all the numbers of the form 1260327937 + 2863311360⋅k.
The smallest composite number in this class is 905, while the first square is 40401.
Roger Crocker proved that there are infinite odd numbers not of the form , with
prime and
0$">.
The first numbers of this kind are 1, 3, 5, 6495105, 848629545, 1117175145, 2544265305,...
The smallest 3 × 3 magic square whose entries are de Polignac numbers is
| 4589 | 10949 | 1649 |
| 2789 | 5729 | 8669 |
| 9809 | 509 | 6869 |
The first de Polignac numbers are 1, 127, 149, 251, 331, 337, 373, 509, 599, 701, 757, 809, 877, 905, 907, 959, 977, 997 more terms
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

A graph displaying how many de Polignac numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

De Polignac numbers can also be... (you may click on names or numbers and on + to get more values)
a-pointer
701
2213
3643
+
99951043
ABA
1856465
aban
127
149
251
+
99000971
abundant
1561875
2012985
2410065
+
49722435
Achilles
704099
757687
1119371
+
97749971
alternating
127
149
509
+
89898941
amenable
149
337
373
+
99999937
apocalyptic
251
977
1019
+
29983
arithmetic
127
149
251
+
9999997
balanced p.
373
977
3637
+
99999617
Bell
877
bemirp
10061
16061681
16880681
+
18999191
binomial
46971
79003
93961
+
99934453
brilliant
1207
1271
1541
+
99400891
c.decagonal
5951
12251
15401
+
99837461
c.heptagonal
2843
3697
4663
+
99823291
c.nonagonal
79003
93961
166753
+
99934453
c.octagonal
40401
62001
96721
+
99620361
c.pentagonal
331
195301
345031
+
99745431
c.square
1985
6161
7813
+
99899113
c.triangular
50509
111385
176989
+
99866161
cake
7807
29317
166751
+
91895351
Carmichael
2465
63973
126217
+
92625121
Carol
959
3967
65023
Chen
127
149
251
+
99999839
congruent
127
149
373
+
9999997
constructible
16843009
cube
205379
226981
389017
+
91733851
Cullen
4718593
20971521
44040193
92274689
Cunningham
127
3845
10001
+
99800099
Curzon
509
809
905
+
99999041
cyclic
127
149
251
+
9999997
D-number
7431
8031
11541
+
7042281
d-powerful
373
2203
2263
+
9994657
decagonal
7267
9457
31417
+
99865045
deceptive
10001
63973
79003
+
98661277
deficient
127
149
251
+
9999997
dig.balanced
149
809
905
+
67078145
Duffinian
905
959
1207
+
9999997
economical
127
149
251
+
19999963
emirp
149
337
701
+
99999343
emirpimes
1211
1243
1807
+
99999937
equidigital
127
149
251
+
19999963
eRAP
182939
247475
1220549
+
99740309
esthetic
4543
4567
8789
+
89878987
Eulerian
65519
evil
149
337
373
+
99999937
fibodiv
149
24719
40331
+
30324247
Fibonacci
1597
121393
514229
Friedman
127
2503
12595
+
979769
frugal
14375
26875
27097
+
99977369
gapful
1207
6161
10021
+
99999755
Gilda
997
18633637
30571351
good prime
127
149
251
+
99904457
happy
331
907
1211
+
9999983
Harshad
2465
4311
6021
+
99996401
heptagonal
9517
96727
101707
+
99026649
hex
127
331
1657
+
99930637
hexagonal
79003
93961
166753
+
99934453
hoax
3505
4855
8023
+
99993307
Hogben
757
1807
17557
+
99930013
Honaker
3433
4153
13217
+
99972317
house
12131
165425
197107
+
81473093
hungry
161449
hyperperfect
1232053
1570153
1618597
+
61599553
iban
127
373
701
+
777701
iccanobiF
792517
inconsummate
1271
1541
1649
+
999931
interprime
1207
1243
3353
+
99999419
junction
509
1207
1211
+
99999857
Kaprekar
94520547
katadrome
6521
7431
8621
+
98654321
Kynea
1087
263167
Lehmer
2465
10963
14611
+
99815821
Leyland
1649
32993
lonely
3967
24281
38501
+
47326801
Lucas
15127
54018521
lucky
127
331
997
+
9999997
m-pointer
15121
61211
1111211
+
61114211
magic
2465
78759
102719
+
80939585
magnanimous
809
2429
2465
+
28862465
metadrome
127
149
1259
+
23456789
modest
509
599
809
+
99901517
Moran
4311
10963
14383
+
99987085
Motzkin
127
nialpdrome
331
877
977
+
99999883
nonagonal
99541
125875
478225
+
96271975
nude
39393
71575
155575
+
97799373
oban
337
373
509
+
997
octagonal
1541
2465
14981
+
97903681
odious
127
251
331
+
99999897
Ormiston
34631
35897
40031
+
99999113
palindromic
373
757
959
+
99944999
palprime
373
757
11411
+
9965699
pancake
1541
1597
2279
+
99962731
panconsummate
127
331
337
pandigital
16405
17735
23935
+
16433683
partition
17977
21637
23338469
pentagonal
17767
20827
31901
+
99825367
pernicious
127
251
331
+
9999997
Pierpont
629857
746497
1492993
86093443
plaindrome
127
149
337
+
88889999
Poulet
2465
31417
41665
+
97255801
power
40401
62001
96721
+
99620361
powerful
40401
62001
96721
+
99620361
prim.abundant
2012985
13777785
16819275
+
96527475
prime
127
149
251
+
99999839
primeval
10079
10237
10379
+
10123579
Proth
1985
5761
7169
+
99893249
repdigit
11111111
repunit
127
757
1807
+
99930013
Rhonda
259333
1583197
2156517
+
98655551
Ruth-Aaron
5405
12727
24433
+
99704375
self
905
1087
1199
+
99999895
self-describing
10143133
10153331
10183133
+
33193117
semiprime
905
959
1199
+
99999937
sliding
10001
48830173
Smith
3505
4855
8023
+
99993307
Sophie Germain
251
509
809
+
99998999
sphenic
2465
4503
4543
+
99999897
square
40401
62001
96721
+
99620361
star
337
23437
31537
+
99267337
straight-line
4567
98765
11111111
23456789
strobogrammatic
6119
10001
18881
+
69911669
strong prime
127
149
251
+
99999839
super-d
127
331
337
+
9999869
tau
40401
62001
660969
+
87665769
taxicab
3242197
5772403
10765603
+
89576767
tetrahedral
302621
366145
657359
+
56677949
tetranacci
14564533
triangular
46971
79003
93961
+
99934453
tribonacci
149
trimorphic
251
499999
7890625
87109375
truncatable prime
337
373
599
+
99336373
twin
149
599
809
+
99996131
uban
1000061
1000099
2000039
+
99000077
Ulam
905
1985
2789
+
10000109
undulating
373
757
959
+
73737373
unprimeable
3505
3665
4195
+
9999775
upside-down
1199
1649
1829
+
99973111
vampire
124483
371893
489955
+
83119297
wasteful
905
959
1199
+
9999997
weak prime
337
509
997
+
99999787
weakly prime
584141
604171
4393139
+
98750609
Wieferich
3837523
Woodall
38879
49151
52487
+
46137343
Zeisel
336611
982513
2263811
+
96931639
Zuckerman
1111117
11111111
zygodrome
1199
7799
44111
+
99996677