Honaker primes

A prime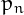

is a Honaker prime if its index $n$

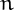and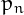

itself have the same sum of digits.

For example, $p_{32}=131$ is a Honaker prime because $3+2=1+3+1$ .

The two smallest Honaker primes $p_n$ for which the sum of the digits is less than the number of digits of $n$ are $p_{1300010120}=30000101111$ and $p_{1000122031021}=30000011223001$ .

$(p_{88}=457, p_{457}=3229)$ is the earliest chain of length 2. Chains of length 3 and 4 start with $p_{248}$ and $p_{496657}$ .

The smallest prime which is Honaker in all the bases from 2 to 10 is $p_{277308991}= 5949670231$ .

The first Honaker primes are 131, 263, 457, 1039, 1049, 1091, 1301, 1361, 1433, 1571, 1913, 1933, 2141, 2221, 2273, 2441 more terms and their indexes are, 32, 56, 88, 175, 176, 182, 212, 218, 227, 248, 293, 295, 323, 331, 338, 362, respectively.

Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

Useful links OEIS, Sequence A033548

Honaker primes can also be... (you may click on names or numbers and on + to get more values)

a-pointer 1933 6301 41131 + 998552251 998963701 aban 131 263 457 + 999000953 999000991 alternating 2141 2707 2729 + 989250121 989252101 amenable 457 1049 1301 + 999822521 999843421 apocalyptic 1301 1933 2273 + 29243 29423 arithmetic 131 263 457 + 9985231 9987001 balanced p. 263 7523 11731 + 999313141 999821261 bemirp 1091 1606081 1806061 + 161080811 169806181 c.decagonal 1361 6301 7411 + 907541281 995531051 c.heptagonal 1933 5741 11173 + 940843471 980855191 c.pentagonal 11731 139831 256801 + 822240901 990472801 c.square 1301 86113 97241 + 942257461 959176201 c.triangular 10711 265231 867541 + 934839391 955548541 Carol 1046527 Chen 131 263 1039 + 99972317 99973061 congruent 263 457 1039 + 9973631 9985231 Cunningham 3137 4357 13457 + 951722501 960752017 Curzon 1049 2141 2273 + 199803041 199820213 cyclic 131 263 457 + 9985231 9987001 d-powerful 2803 4153 4397 + 9921473 9972233 de Polignac 3433 4153 13217 + 99970391 99972317 deficient 131 263 457 + 9985231 9987001 dig.balanced 2141 2221 2707 + 199805003 199805033 economical 131 263 457 + 19984501 19984511 emirp 1091 1301 1913 + 199803013 199901021 equidigital 131 263 457 + 19984501 19984511 esthetic 34543 3212123 343456543 565454543 Eulerian 67108837 evil 263 1049 1091 + 999810311 999831103 fibodiv 1301 67645819 123047543 Friedman 58921 64513 78163 + 902507 902563 good prime 3433 4903 6563 + 198464323 199022107 happy 263 1039 1933 + 9940703 9982211 hex 126691 333667 436627 + 961068907 972162007 Hogben 5701 8011 98911 + 954779101 975906361 iban 1301 2141 2221 + 773147 773273 inconsummate 1049 1571 2591 + 991619 996011 junction 2719 4723 5009 + 99954541 99954551 lucky 1039 1933 2221 + 9971341 9985231 magnanimous 2221 8821 40427 + 2666021 6600227 metadrome 457 12347 13457 modest 1433 1933 5009 + 997001221 998111111 nialpdrome 2221 6311 6553 + 998773211 998831111 odious 131 457 1039 + 999822521 999843421 Ormiston 1913 35617 48109 + 998779031 999003913 palindromic 131 16661 33533 + 981151189 982323289 palprime 131 16661 33533 + 981151189 982323289 pancake 13367 24091 64621 + 950981467 960424879 pernicious 131 457 1039 + 9983203 9985231 plaindrome 457 3559 12277 + 333444679 345555569 prime 131 263 457 + 999831103 999843421 primeval 100279 Proth 3137 57089 64513 + 949420033 955383809 repunit 5701 8011 98911 + 954779101 975906361 self 457 2729 3067 + 999632021 999831103 self-describing 18331031 19143133 19143331 21183223 Sophie Germain 131 1049 2141 + 999412313 999821261 star 11353 15913 20533 + 955359253 981120937 strobogrammatic 111689111 160609091 166080991 + 661000199 666101999 strong prime 457 1049 1091 + 99972221 99972703 super-d 131 1049 2591 + 9973631 9985231 truncatable prime 3137 4397 6353 + 627543853 915613967 twin 1049 1091 1301 + 999611309 999815041 uban 17000077 26000069 37000097 + 63000089 77000081 Ulam 131 1433 4153 + 9962321 9973021 undulating 131 upside-down 7283 11473699 13191979 + 96637441 98746321 weak prime 131 1039 1433 + 99972317 99973061 weakly prime 6173731 20212327 22138349 + 944375701 945808223 zygodrome 22277 77711 1144499 + 994400333 999112211