[go: up one dir, main page]
Search a number
cyclic numbers
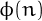A number  $n$  is a cyclic number if  $n$  and  $\phi(n)$  have no common prime factors.

If follows from the definition of  $\phi(n)$  that all prime numbers are cyclic, that the only even cyclic number is 2, and that all cyclic numbers are squarefree.

It is known that the divisors of Carmichael numbers are all odd cyclic numbers. G.P. Michon has conjectured that the the converse also holds, i.e., for each odd cyclic number  $c$  there are infinite Carmichael numbers which are divisible by  $c$.

The smallest 3 × 3 magic square whose entries are consecutive cyclic numbers is

265247259
251257263
255267249

Below, the spiral pattern of cyclic numbers up to  $100^2$. See the page on prime numbers for an explanation and links to similar pictures.

spiral pattern of cyclic numbers

The first cyclic numbers are 1, 2, 3, 5, 7, 11, 13, 15, 17, 19, 23, 29, 31, 33, 35, 37, 41, 43, 47, 51, 53, 59 more terms

Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
remainders of cyclic numbers

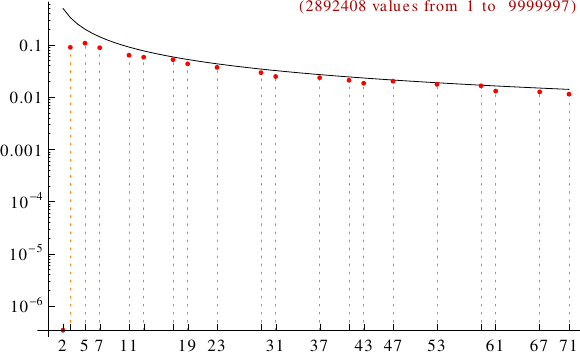
A graph displaying how many cyclic numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.
divisibility of cyclic numbers
Useful links Wikipedia, Cyclic number
OEIS, Sequence A003277
Cyclic numbers can also be... (you may click on names or numbers and on + to get more values)

a-pointer 11 13 101 + 9999347 aban 11 13 15 + 9000997 alt.fact. 19 101 619 + 3301819 alternating 23 29 41 + 9898985 amenable 13 17 29 + 9999997 apocalyptic 157 247 251 + 29999 arithmetic 11 13 15 + 9999997 astonishing 15 1353 23287 78403 balanced p. 53 157 173 + 9999937 Bell 15 877 4213597 bemirp 1061 1091 1601 + 1909081 binomial 15 35 91 + 9992685 brilliant 15 35 143 + 9999811 c.decagonal 11 31 61 + 9989911 c.heptagonal 43 71 197 + 9978613 c.nonagonal 91 595 703 + 9916831 c.pentagonal 31 51 141 + 9965031 c.square 13 41 61 + 9994921 c.triangular 19 31 85 + 9988471 cake 15 299 697 + 9735503 Canada 581 8549 16999 Carmichael 561 1105 1729 + 9890881 Carol 47 223 959 + 1046527 Chen 11 13 17 + 9999991 congruent 13 15 23 + 9999997 constructible 15 17 51 + 5570645 Cullen 65 161 2049 + 4718593 Cunningham 15 17 31 + 9998243 Curzon 29 33 41 + 9999869 D-number 15 33 51 + 7043109 d-powerful 43 89 209 + 9999827 de Polignac 127 149 251 + 9999997 decagonal 85 451 1105 + 9968227 deceptive 91 259 451 + 9989161 deficient 11 13 15 + 9999997 dig.balanced 11 15 19 + 9999989 double fact. 15 Duffinian 35 65 77 + 9999997 economical 11 13 15 + 9999991 emirp 13 17 31 + 9999971 emirpimes 15 51 85 + 9999967 equidigital 11 13 15 + 9999991 eRAP 4233 21385 26123 + 9960047 esthetic 23 43 65 + 9898789 Eulerian 11 247 1013 + 4194281 evil 15 17 23 + 9999989 fibodiv 19 47 61 + 9166661 Fibonacci 13 89 233 + 5702887 Friedman 127 347 1285 + 999163 gapful 143 187 341 + 9999985 Gilda 29 683 997 + 3970547 good prime 11 17 29 + 9993337 happy 13 19 23 + 9999991 Harshad 133 209 247 + 9999881 heptagonal 235 403 469 + 9967027 hex 19 37 61 + 9997351 hexagonal 15 91 435 + 9934653 hoax 85 265 319 + 9999895 Hogben 13 31 43 + 9982441 Honaker 131 263 457 + 9987001 house 271 933 1285 + 9716393 hungry 17 2003 37929 + 2401519 hyperperfect 697 1333 1909 + 9699181 iban 11 17 23 + 777773 iccanobiF 13 4139 61135 792517 idoneal 13 15 33 + 345 inconsummate 65 95 161 + 999995 interprime 15 69 217 + 9999895 Jacobsthal 11 43 85 + 2796203 junction 101 103 107 + 9999959 Kaprekar 703 4879 7777 + 5479453 katadrome 31 41 43 + 9876541 Kynea 23 79 287 + 4198399 Lehmer 15 51 85 + 9997351 Leyland 17 145 177 + 4785713 lonely 23 53 211 + 4652429 Lucas 11 29 47 + 4870847 lucky 13 15 31 + 9999997 Lynch-Bell 15 m-pointer 23 61 1123 + 9111341 magic 15 65 671 + 9951391 magnanimous 11 23 29 + 8844449 metadrome 13 15 17 + 2356789 modest 13 19 23 + 9989999 Moran 133 209 247 + 9999881 Motzkin 51 127 323 + 853467 narcissistic 371 407 9926315 nialpdrome 11 31 33 + 9999997 nonagonal 559 1639 3729 + 9944871 nude 11 15 33 + 7771771 oban 11 13 15 + 997 octagonal 65 133 341 + 9900833 odious 11 13 19 + 9999997 Ormiston 1913 1931 18379 + 9994631 palindromic 11 33 77 + 9998999 palprime 11 101 131 + 9989899 pancake 11 29 37 + 9997157 panconsummate 11 15 23 + 3097 pandigital 11 15 19 + 9997981 partition 11 15 77 + 9289091 pentagonal 35 51 145 + 9967837 pernicious 11 13 17 + 9999997 Perrin 17 29 51 + 6900995 Pierpont 13 17 19 + 8503057 plaindrome 11 13 15 + 8999999 Poulet 341 561 1105 + 9920401 prime 11 13 17 + 9999991 primeval 13 37 107 + 1234679 Proth 13 17 33 + 9994241 rare 65 repdigit 11 33 77 + 5555555 repfigit 19 47 61 + 7913837 repunit 13 15 31 + 9982441 Rhonda 35581 47265 54479 + 9214557 Ruth-Aaron 15 77 493 + 9997417 Sastry 40495 self 31 53 97 + 9999965 semiprime 15 33 35 + 9999997 sliding 11 29 65 + 9766649 Smith 85 265 319 + 9999895 Sophie Germain 11 23 29 + 9999653 sphenic 255 345 435 + 9999985 star 13 37 73 + 9992341 straight-line 123 159 321 + 7654321 strobogrammatic 11 69 101 + 6998669 strong prime 11 17 29 + 9999971 subfactorial 265 14833 super-d 19 31 69 + 9999931 taxicab 1729 20683 149389 + 9443761 tetrahedral 35 455 9139 + 9886435 tetranacci 15 29 401 + 20569 triangular 15 91 435 + 9992685 tribonacci 13 149 121415 trimorphic 51 249 251 + 4999999 truncatable prime 13 17 23 + 9986113 twin 11 13 17 + 9999973 uban 11 13 15 + 9000097 Ulam 11 13 47 + 9999977 undulating 101 131 141 + 9595959 unprimeable 515 535 895 + 9999985 upside-down 19 37 73 + 9985211 vampire 117067 124483 146137 + 536539 wasteful 33 51 65 + 9999997 weak prime 13 19 23 + 9999991 weakly prime 294001 505447 584141 + 9931447 Wieferich 1093 3511 3837523 Woodall 17 23 159 + 9961471 Zeisel 1729 1885 4505 + 9773731 Zuckerman 11 15 115 + 1111117 zygodrome 11 33 77 + 9999977