Lucas numbers

Lucas numbers are defined by the recurrence $L_0=2$

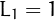and $L_n=L_{n-1}+L_{n-2}$ for

1$">, so are similar to Fibonacci numbers, but with a different starting point.

Their closed form is

$L_n =\left(\frac{1+\sqrt{5}}{2}\right)^n+\left(\frac{1-\sqrt{5}}{2}\right)^n$

Two interesting sums (the first for any integer $\alpha\ge2$ ):

$\sum_{k=1}^{\infty}\frac{L_k}{\alpha^k} = \frac{\alpha+2}{\alpha^2-\alpha-1}\,,\quad\quad \sum_{k=0}^{\infty}\frac{L_k}{k!} =\frac{1+e^{\sqrt{5}}}{\sqrt{e^{\sqrt{5}-1}}}\,.$

The first Lucas numbers are 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843, 1364, 2207, 3571, 5778, 9349, 15127, 24476, 39603 more terms

Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

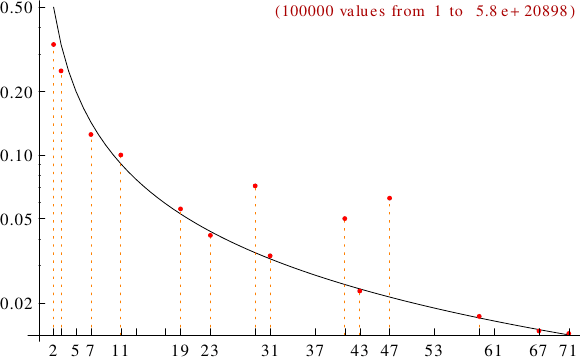
A graph displaying how many Lucas numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Useful links Mathworld, Lucas Number
Wikipedia, Lucas number
OEIS, Sequence A000032

Lucas numbers can also be... (you may click on names or numbers and on + to get more values)

a-pointer 11 ABA 18 aban 11 18 29 47 76 123 199 322 521 843 abundant 18 5778 1860498 alternating 18 29 47 76 123 521 3010349 amenable 29 76 521 1364 9349 24476 167761 439204 3010349 7881196 54018521 141422324 969323029 apocalyptic 9349 15127 24476 arithmetic 11 29 47 123 199 322 521 843 1364 2207 + 710647 1149851 3010349 4870847 automorphic 76 binomial 5778 brilliant 64079 4870847 c.decagonal 11 c.pentagonal 76 c.triangular 199 Carol 47 Chen 11 29 47 199 521 2207 3010349 congruent 29 47 199 1364 2207 9349 15127 24476 64079 103682 710647 3010349 4870847 Curzon 18 29 3010349 54018521 cyclic 11 29 47 123 199 521 843 2207 3571 9349 + 167761 1149851 3010349 4870847 D-number 123 843 271443 d-powerful 1364 de Polignac 15127 54018521 deficient 11 29 47 76 123 199 322 521 843 1364 + 1149851 3010349 4870847 7881196 dig.balanced 11 167761 Duffinian 15127 39603 64079 167761 271443 1149851 4870847 economical 11 29 47 123 199 521 2207 3571 9349 15127 271443 1149851 3010349 12752043 emirp 199 3571 9349 3010349 emirpimes 123 15127 64079 equidigital 11 29 47 123 199 521 2207 3571 9349 15127 271443 1149851 3010349 12752043 esthetic 76 123 Eulerian 11 evil 18 29 123 843 5778 24476 103682 439204 1860498 54018521 599074578 fibodiv 47 199 Friedman 103682 gapful 167761 1860498 20633239 Gilda 29 2207 good prime 11 29 happy 1860498 Harshad 18 322 5778 heptagonal 18 hex 3571 hexagonal 5778 hoax 7881196 iban 11 47 123 322 2207 271443 idoneal 18 inconsummate 521 2207 103682 271443 interprime 18 76 1364 33385282 Jacobsthal 11 junction 521 katadrome 76 521 843 Lehmer 167761 lucky 3571 9349 710647 magnanimous 11 29 47 76 metadrome 18 29 47 123 modest 29 199 Moran 18 nialpdrome 11 76 322 521 843 nude 11 oban 11 18 29 76 odious 11 47 76 199 322 521 1364 2207 3571 9349 + 141422324 228826127 370248451 969323029 palindromic 11 167761 palprime 11 pancake 11 29 3571 panconsummate 11 18 pandigital 11 partition 11 pernicious 11 18 47 76 199 322 521 1364 2207 9349 + 271443 1149851 4870847 7881196 Perrin 29 plaindrome 11 18 29 47 123 199 5778 practical 18 5778 prim.abundant 18 prime 11 29 47 199 521 2207 3571 9349 3010349 54018521 370248451 6643838879 119218851371 pseudoperfect 18 5778 repdigit 11 repfigit 47 self 15127 39603 3010349 4870847 141422324 semiprime 123 843 15127 64079 271443 1149851 4870847 87403803 sliding 11 29 Sophie Germain 11 29 3010349 54018521 sphenic 322 39603 103682 167761 12752043 straight-line 123 strobogrammatic 11 strong prime 11 29 521 3571 54018521 super-d 15127 64079 1860498 3010349 7881196 tau 18 tetranacci 29 triangular 5778 trimorphic 76 truncatable prime 29 47 twin 11 29 199 521 uban 11 18 29 47 76 Ulam 11 18 47 167761 1149851 unprimeable 322 439204 1860498 untouchable 322 5778 wasteful 18 76 322 843 1364 5778 24476 39603 64079 103682 + 710647 1860498 4870847 7881196 weak prime 47 199 2207 9349 3010349 Zuckerman 11 Zumkeller 5778 zygodrome 11