Catalan numbers

The

-th Catalan number $C_n$

can be defined as

$C_n = \frac{1}{n}{2n\choose n} = \frac{(2n)!}{n!(n+1)!}\,.$

Catalan numbers have many combinatorial interpretations. For example, $C_n$ is the number of ways a regular $n$ -gon can be divided into $n-2$ triangles taking into account different orientations as distinct. See also the picture aside.

The only odd Catalan numbers $C_n$ are those where $n=2^k-1$ .

Two interesting sums involving Catalan numbers:

$\sum_{k=1}^{\infty}\frac{1}{C_k}=1+\frac{4 \pi }{9 \sqrt{3}}\,,\quad\quad% \sum_{k=1}^{\infty}\frac{C_k}{4^k}=1\,.$

The first Catalan numbers are 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670 more terms

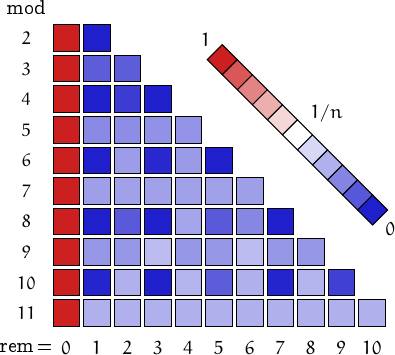
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

A graph displaying how many Catalan numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Useful links Mathworld, Catalan Number
Wikipedia, Catalan number
OEIS, Sequence A000108

Catalan numbers can also be... (you may click on names or numbers)

aban 14 42 132 429 abundant 42 132 1430 16796 58786 208012 742900 2674440 9694845 35357670 admirable 42 alternating 14 1430 amenable 132 429 16796 208012 742900 2674440 9694845 477638700 apocalyptic 4862 16796 arithmetic 14 42 132 429 1430 4862 16796 58786 208012 742900 2674440 9694845 astonishing 429 brilliant 14 cake 42 congruent 14 429 1430 4862 16796 58786 742900 9694845 Curzon 14 429 1430 9694845 35357670 129644790 d-powerful 132 deficient 14 429 4862 dig.balanced 42 58786 35357670 eban 42 economical 14 equidigital 14 evil 132 429 1430 16796 58786 208012 742900 9694845 477638700 fibodiv 14 gapful 132 1430 2674440 9694845 35357670 129644790 1767263190 6564120420 24466267020 happy 16796 9694845 Harshad 42 132 58786 9694845 477638700 1767263190 6564120420 iban 14 42 idoneal 42 inconsummate 4862 interprime 42 junction 208012 katadrome 42 lucky 429 Lynch-Bell 132 magnanimous 14 metadrome 14 Moran 42 nialpdrome 42 nude 132 odious 14 42 4862 2674440 35357670 129644790 panconsummate 14 partition 42 pernicious 14 42 132 plaindrome 14 practical 42 132 208012 742900 2674440 prim.abundant 42 1430 16796 58786 pronic 42 132 pseudoperfect 42 132 1430 16796 58786 208012 742900 repfigit 14 self 42 132 9694845 semiprime 14 Smith 9694845 sphenic 42 429 tau 132 uban 42 Ulam 429 unprimeable 16796 208012 2674440 wasteful 42 132 429 1430 4862 16796 58786 208012 742900 2674440 9694845 Zuckerman 132 Zumkeller 42 132 1430 16796 58786