Given a number 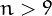 9$"> with digits
9$"> with digits  , let us
define a Fibonacci-like sequence where
, let us
define a Fibonacci-like sequence where
![\[
a(1)=|d_1-d_2-\cdots-d_k|\,,\quad\quad a(2)=d_1+d_2+\cdots+d_k\,,
\]](https://speed.lescigales.org/xypor/index.php?q=aHR0cHM6Ly93d3cubnVtYmVyc2FwbGVudHkuY29tL3NldC9HaWxkYV9udW1iZXIvcGljLjMucG5n) and
and 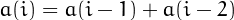 for
for 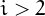 2$">. If the number
2$">. If the number 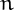 appear in the sequence
of the
appear in the sequence
of the 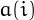 's then
's then  is called Gilda number.
is called Gilda number.
For example, starting with n=152 we have the sequence |1-5-2|=6, 1+5+2=8, then 14, 22, 36, 58, 94, and finally 152.
The first Gilda numbers are 29, 49, 78, 110, 152, 220, 314, 330, 364, 440, 550, 628, 660, 683, 770, 880, 990, 997 more terms
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

A graph displaying how many Gilda numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Useful links
OEIS, Sequence A042947
Gilda numbers can also be... (you may click on names or numbers and on + to get more values)
aban
29
49
78
110
152
220
314
330
364
440
+
770
880
990
997
abundant
78
220
330
364
440
550
660
770
880
990
+
933138
3120796
3363582
14005576
admirable
78
364
3363582
alternating
29
49
78
65676
amenable
29
49
152
220
364
440
628
660
880
997
+
4484776
14005576
18633637
92078232
amicable
220
apocalyptic
220
660
5346
13064
arithmetic
29
49
78
110
220
330
550
660
683
770
+
3606368
3727761
3970547
4848955
binomial
78
220
330
364
990
brilliant
49
c.octagonal
49
Chen
29
683
2207
congruent
29
78
110
152
220
330
440
550
628
660
+
3120796
3242189
3363582
3606368
Cunningham
440
Curzon
29
78
330
30254
977909
cyclic
29
683
997
2207
73805
977909
3242189
3970547
d-powerful
65676
4848955
de Polignac
997
18633637
30571351
deficient
29
49
110
152
314
628
683
997
2207
13064
+
3849154
3970547
4484776
4848955
dig.balanced
49
78
550
628
660
880
990
35422
38006
202196
933138
14005576
Duffinian
49
977909
3242189
3970547
4848955
economical
29
49
683
997
2207
4848955
emirpimes
49
314
3242189
equidigital
29
49
683
997
2207
4848955
esthetic
78
65676
evil
29
78
330
550
660
683
990
5346
35422
38006
+
18633637
30571351
34610158
786119998
gapful
110
220
330
440
550
660
770
880
990
1377313380
good prime
29
happy
49
440
683
5346
38006
3606368
4848955
Harshad
110
152
220
330
364
440
550
660
770
880
+
3606368
1377313380
9142471346
9410385642
hoax
364
660
house
78
iban
110
220
314
440
770
2207
idoneal
78
330
inconsummate
2207
5346
30254
37862
38006
933138
interprime
660
3727761
Jacobsthal
683
junction
35422
18633637
92078232
Lucas
29
2207
lucky
49
997
magnanimous
29
49
110
152
683
metadrome
29
49
78
modest
29
49
Moran
152
30254
nialpdrome
110
220
330
440
550
660
770
880
990
997
O'Halloran
660
oban
29
78
330
550
628
660
683
770
880
990
997
odious
49
110
152
220
314
364
440
628
770
880
+
3849154
4848955
92078232
271953103
pancake
29
panconsummate
78
pandigital
78
990
pentagonal
330
pernicious
49
110
152
220
314
364
440
628
770
880
997
2207
13064
3849154
Perrin
29
plaindrome
29
49
78
power
49
powerful
49
practical
78
220
330
364
440
660
880
990
5346
prim.abundant
78
364
550
3363582
prime
29
683
997
2207
30571351
271953103
pronic
110
Proth
49
pseudoperfect
78
220
330
364
440
550
660
770
880
990
5346
65676
933138
repunit
364
Ruth-Aaron
49
78
self
110
semiprime
49
314
977909
3242189
4848955
sliding
29
110
Sophie Germain
29
683
sphenic
78
110
30254
35422
37862
38006
73805
143662
3363582
3727761
3849154
3970547
square
49
strong prime
29
30571351
super Niven
110
220
330
440
550
660
770
880
990
super-d
35422
3363582
4484776
tau
152
880
4484776
tetrahedral
220
364
tetranacci
29
triangular
78
990
trimorphic
49
truncatable prime
29
683
997
twin
29
uban
29
49
78
unprimeable
628
38006
73805
202196
933138
3606368
untouchable
628
5346
65676
202196
wasteful
78
110
152
220
314
330
364
440
550
628
+
3727761
3849154
3970547
4484776
weak prime
683
997
2207
Zumkeller
78
220
330
364
440
550
660
770
880
990
5346
65676