A prime is said to be balanced if it
is the average of the two surrounding primes, i.e., it is at equal distance from previous prime and next prime.
For example, 53 is a balanced prime since it is the average of the two primes 47 and 59.
The smallest 3 × 3 magic square made of balanced primes is
| 6602423 | 31893539 | 16675727 |
| 28463867 | 18390563 | 8317259 |
| 20105399 | 4887587 | 30178703 |
The first balanced primes are 5, 53, 157, 173, 211, 257, 263, 373, 563, 593, 607, 653, 733, 947, 977, 1103, 1123, 1187, 1223, 1367, 1511 more terms
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
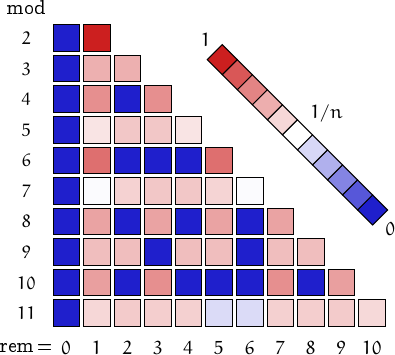
Balanced primes can also be... (you may click on names or numbers and on + to get more values)
aban
53
157
173
211
257
+
9999000689
alternating
563
947
2903
2963
6323
+
989892367
amenable
53
157
173
257
373
+
999998789
apocalyptic
157
977
1103
1753
2287
+
29873
arithmetic
53
157
173
211
257
+
9999937
bemirp
18616681
168910801
199109681
1088900611
1161111661
+
1969081091
c.decagonal
211
20161
135301
183361
286801
+
9897022951
c.heptagonal
176401
890821
1545461
1578193
8262913
+
9583951693
c.pentagonal
11731
17431
17851
839551
8868931
+
9482550391
c.square
15313
20201
156241
353641
1035361
+
9992597081
c.triangular
412651
1282051
4670191
7395931
7876459
+
9787991431
Chen
53
157
211
257
263
+
99999617
congruent
53
157
173
257
263
+
9997327
constructible
257
Cunningham
257
13457
30977
33857
98597
+
9748402757
Curzon
53
173
593
653
4409
+
199999661
cyclic
53
157
173
211
257
+
9999937
d-powerful
373
17483
22447
23327
26393
+
9923477
de Polignac
373
977
3637
4013
4691
+
99999617
deficient
53
157
173
211
257
+
9999937
dig.balanced
563
653
2417
7823
7841
+
199987841
economical
53
157
173
211
257
+
19999981
emirp
157
733
1103
1223
1511
+
199999661
equidigital
53
157
173
211
257
+
19999981
esthetic
34543
432343
3212323
5434343
343232101
+
6789898987
evil
53
257
263
373
593
+
999998789
fibodiv
123047543
Friedman
19739
74897
128153
156241
161053
+
885727
good prime
53
257
563
593
733
+
199880953
happy
263
563
653
1511
2417
+
9996823
hex
22447
35317
45757
73477
151201
+
9974545747
Hogben
157
211
1123
3307
5113
+
9945973171
Honaker
263
7523
11731
13457
15193
+
999821261
iban
173
211
373
1103
1123
+
777103
inconsummate
173
563
3307
3733
4409
+
993869
junction
6317
6323
7823
8117
10607
+
99986251
katadrome
53
653
9871
96431
Leyland
593
32993
lonely
53
211
lucky
211
1123
3307
3313
4993
+
9983977
m-pointer
1123
21911
3116111
11413111
12111331
+
1111131821
magnanimous
607
42209
metadrome
157
257
1367
13457
12356789
modest
211
733
23333
29333
40111
+
1999002079
nialpdrome
53
211
653
733
977
+
9999997543
oban
53
373
563
593
607
+
977
odious
157
173
211
563
607
+
999996329
Ormiston
34631
66431
76579
122579
145879
+
1999965379
palindromic
373
11411
30103
34543
35753
+
996989699
palprime
373
11411
30103
34543
35753
+
996989699
pancake
211
947
4657
9871
40471
+
9999313237
panconsummate
53
211
257
pernicious
157
173
211
257
563
+
9997219
Pierpont
257
18433
plaindrome
157
257
1123
1223
1367
+
6888899999
prime
53
157
173
211
257
+
9999997543
primeval
1367
Proth
257
4993
9473
18433
30977
+
9963962369
repunit
157
211
1123
3307
5113
+
9945973171
self
53
211
1223
3313
5113
+
999979397
self-describing
17331031
21322319
32272733
1341441841
1722311033
+
4442274227
Sophie Germain
53
173
593
653
1103
+
9999994883
star
3313
12973
15913
986581
1527121
+
9942603337
strobogrammatic
688889
1068901
1681891
11896811
166906991
+
1906699061
super-d
1123
4013
4597
5113
7823
+
9997219
truncatable prime
53
173
373
593
653
+
9391564373
uban
53
1000099
6000047
7000003
7000033
+
9099000013
Ulam
53
607
1103
4409
7583
+
9992681
undulating
373
upside-down
7823
92581
3355577
14991169
16746349
+
9882648221
weakly prime
3326489
21089489
21668839
27245539
38178211
+
9994090871
zygodrome
3355577
5555777
7722277
7799333
8884433
+
9993355511