The factorial of an integer 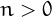 0$">, denoted by n!, is the product of all the
integers from 1 to
0$">, denoted by n!, is the product of all the
integers from 1 to 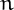 . By definition,
. By definition, 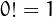 .
.
![\[\sum_{k=0}^{\infty}\frac{1}{k!}=e,\quad\quad
\sum_{k=0}^{\infty}(-1)^k\frac{1}{k!}=\frac{1}{e}\,.\]](https://speed.lescigales.org/xypor/index.php?q=aHR0cHM6Ly93d3cubnVtYmVyc2FwbGVudHkuY29tL3NldC9mYWN0b3JpYWwvcGljLjYucG5n)
For example, .
The number of permutations of objects is
.
Factorials are involved in many classic formulas, like
The first factorials are 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800, 39916800, 479001600, 6227020800, 87178291200 more terms
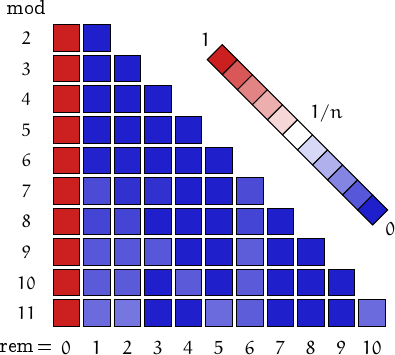
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
Factorials can also be... (you may click on names or numbers)
ABA
24
aban
24
120
720
abundant
24
120
720
5040
40320
362880
3628800
39916800
admirable
24
120
amenable
24
120
720
5040
40320
362880
3628800
39916800
479001600
apocalyptic
720
binomial
120
compositorial
24
congruent
24
120
720
40320
362880
3628800
constructible
24
120
Cunningham
24
120
5040
d-powerful
24
dig.balanced
120
3628800
economical
362880
3628800
equidigital
362880
3628800
eRAP
24
Eulerian
120
evil
24
120
720
5040
40320
362880
479001600
gapful
120
40320
362880
3628800
39916800
479001600
6227020800
87178291200
Harshad
24
120
720
5040
40320
362880
3628800
39916800
479001600
6227020800
hexagonal
120
highly composite
24
120
720
5040
iban
24
120
720
40320
idoneal
24
120
inconsummate
362880
interprime
120
3628800
Jordan-Polya
24
120
720
5040
40320
362880
3628800
39916800
479001600
6227020800
87178291200
1307674368000
20922789888000
355687428096000
katadrome
720
lonely
120
Lynch-Bell
24
metadrome
24
nialpdrome
720
nonagonal
24
nude
24
oban
720
odious
3628800
39916800
panconsummate
24
pandigital
120
pernicious
24
3628800
plaindrome
24
practical
24
120
720
5040
40320
362880
3628800
pseudoperfect
24
120
720
5040
40320
362880
Ruth-Aaron
24
super Niven
24
120
5040
40320
superabundant
24
120
720
5040
tau
24
720
5040
40320
362880
3628800
39916800
479001600
tetrahedral
120
triangular
120
tribonacci
24
trimorphic
24
Ulam
720
unprimeable
5040
40320
362880
3628800
untouchable
120
40320
362880
wasteful
24
120
720
5040
40320
Zuckerman
24
Zumkeller
24
120
720
5040
40320