enlightened numbers

A number

is said to be enlightened if it begins with the concatenation of its distinct prime factors.

For example, 2500 is enlightened since its factorization is 2²⋅5⁴ and indeed its begins with '25'.

The smallest member with 4 prime factors is 2377970784 = $2^5*3^5*7^2*79^2$ .

The first enlightened numbers are 250, 256, 2048, 2176, 2304, 2500, 2560, 2744, 23328, 25000, 25600, 119911, 219488, 236196, 250000, 256000, 262144, 290912, 2097152, 2238728, 2317312, 2359296 more terms

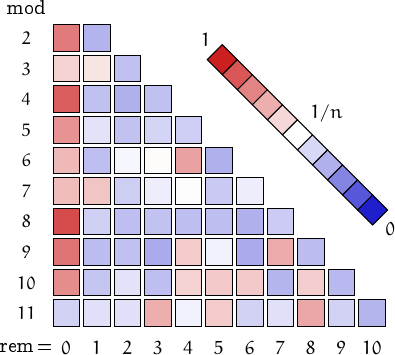
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

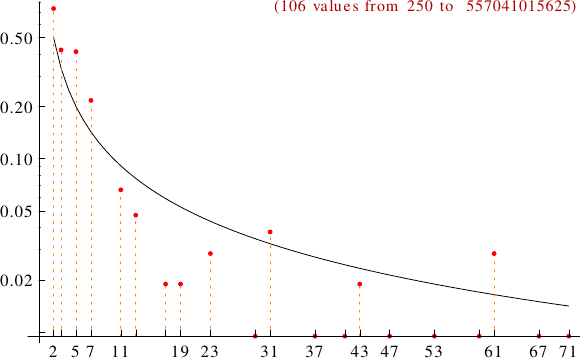
A graph displaying how many enlightened numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Useful links Joseph L. Pe, The Enlightened Numbers
OEIS, Sequence A069154

Enlightened numbers can also be... (you may click on names or numbers and on + to get more values)

ABA 2048 2500 23328 262144 2097152 2238728 + 250000000000 274877906944 323754489243 361881028863 aban 250 256 25000000 250000000 256000000 2500000000 + 25000000000 25600000000 250000000000 256000000000 abundant 2176 2304 2500 2560 2744 23328 + 23887872 25000000 25600000 27294568 Achilles 23328 25000 219488 256000 2238728 2370816 + 257357187500 323754489243 351353851875 361881028863 alternating 250 256 amenable 256 2048 2176 2304 2500 2560 + 275365888 387420489 595238125 761743661 apocalyptic 2304 2500 23328 25000 25600 arithmetic 2744 219488 290912 5117695 c.octagonal 3515625 387420489 3486784401 31381059609 37822859361 137858491849 c.pentagonal 2176 cake 2048 congruent 2176 2744 119911 219488 290912 2317312 2370816 3720087 5117695 constructible 256 2048 2176 2560 262144 2097152 268435456 2147483648 274877906944 cube 2744 262144 2097152 23887872 387420489 57736239625 231928233984 373714754427 d-powerful 2048 2238728 deficient 250 256 2048 119911 262144 290912 + 2238728 3515625 3720087 5117695 dig.balanced 2744 236196 250000 Duffinian 256 2048 2304 2500 25600 119911 + 2359296 2560000 3515625 3720087 economical 250 256 2048 2176 2304 2500 + 3515625 3720087 5117695 13436683 equidigital 250 2176 2304 2500 2744 25600 119911 290912 2317312 5117695 evil 250 2176 2304 2560 2744 23328 + 353109375 387420489 595238125 761743661 Friedman 2048 2500 23328 236196 250000 262144 frugal 256 2048 2560 23328 25000 219488 + 358722675 387420489 595238125 761743661 gapful 2304 2500 2560 25000 25600 119911 + 23592960000 25000000000 25600000000 25711938560 happy 219488 236196 Harshad 2176 2304 23328 219488 236196 2359296 + 237180384 358722675 2359296000 2377970784 hoax 250 2500 25000 250000 2500000 25000000 iban 2304 2744 impolite 256 2048 262144 2097152 268435456 2147483648 274877906944 inconsummate 236196 290912 Jordan-Polya 256 2048 2304 262144 2097152 2359296 + 2147483648 23219011584 231928233984 274877906944 junction 2238728 lucky 119911 3720087 metadrome 256 Moran 29090912 nude 2744 23328 236196 odious 256 2048 2500 25600 236196 250000 + 268435456 271351808 275365888 358722675 palindromic 119911 pernicious 2176 2304 2500 2560 25600 250000 2317312 2359296 2560000 plaindrome 256 power 256 2048 2304 2500 2744 25600 + 231928233984 250000000000 274877906944 373714754427 powerful 256 2048 2304 2500 2744 23328 + 323754489243 351353851875 361881028863 373714754427 practical 256 2048 2176 2304 2500 2560 + 2359296 2370816 2500000 2560000 pseudoperfect 2176 2304 2500 2560 2744 23328 + 219488 236196 250000 256000 self 2560 23328 2317312 2359296 2370816 3720087 5117695 358722675 sliding 250 2500 25000 250000 2500000 25000000 250000000 2500000000 25000000000 250000000000 square 256 2304 2500 25600 236196 250000 + 37822859361 137858491849 250000000000 274877906944 super-d 2097152 5117695 tau 2176 2560 2370816 23592960 27294568 237180384 250000000 uban 25000000 25000000000 Ulam 25000 119911 2500000 5117695 unprimeable 2048 2560 25000 219488 236196 256000 + 2317312 2359296 2560000 5117695 untouchable 2048 2304 2500 25000 25600 236196 250000 Zuckerman 23328 Zumkeller 2176 2560 2744 25000 zygodrome 119911