Let 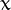 be a number of
be a number of  digits. Let us define a Fibonacci-like sequence using as seeds the digits of
digits. Let us define a Fibonacci-like sequence using as seeds the digits of 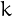 and then at each step
adding the last
and then at each step
adding the last  terms. If
terms. If 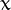 itself appears in the sequence, then it is a repfigit number.
itself appears in the sequence, then it is a repfigit number.
Fibodiv numbers are also named Keith numbers.
For example, 1104 is a repfigit or Keith number because the resulting sequence 1, 1, 0, 4, 6, 11, 21, 42, 80, 154, 297, 573, 1104, contains 1104.
Note that the 6 repfigit numbers with 2 digits are, by definition, fibodiv numbers, too.
The first repfigit numbers are 14, 19, 28, 47, 61, 75, 197, 742, 1104, 1537, 2208, 2580, 3684, 4788, 7385, 7647, 7909, 31331, 34285, 34348, 55604, 62662, 86935, 93993, 120284 more terms
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
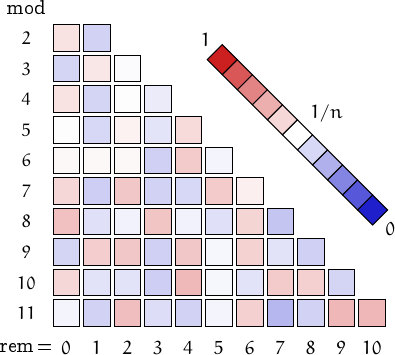
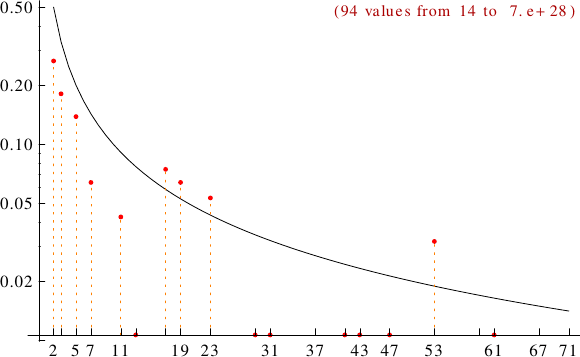
A graph displaying how many repfigit numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.
Repfigit numbers can also be... (you may click on names or numbers and on + to get more values)
aban
14
19
28
47
61
75
197
742
abundant
1104
2208
2580
3684
4788
147640
174680
183186
298320
694280
33445755
alt.fact.
19
alternating
14
47
61
amenable
28
61
197
1104
1537
2208
2580
3684
4788
7385
+
925993
7913837
129572008
251133297
apocalyptic
3684
4788
7385
7647
7909
arithmetic
14
19
47
61
197
742
1537
2208
2580
7385
+
355419
925993
1084051
7913837
betrothed
75
binomial
28
brilliant
14
1537
c.decagonal
61
c.heptagonal
197
c.nonagonal
28
c.square
61
c.triangular
19
Carol
47
Catalan
14
Chen
19
47
197
1084051
congruent
14
28
47
61
197
742
1104
2208
2580
4788
+
147640
174680
298320
7913837
Cunningham
28
197
2208
Curzon
14
7385
93993
cyclic
19
47
61
197
1537
7647
7909
31331
34285
86935
925993
1084051
7913837
D-number
7647
d-powerful
62662
decagonal
742
deficient
14
19
47
61
75
197
742
1537
7385
7647
+
355419
925993
1084051
7913837
dig.balanced
19
75
197
742
3684
55604
156146
183186
298320
Duffinian
75
1537
7385
7909
31331
34285
86935
925993
7913837
economical
14
19
47
61
197
1537
34285
129106
1084051
emirp
1084051
emirpimes
7909
7913837
equidigital
14
19
47
61
197
1537
34285
129106
1084051
eRAP
1104
evil
75
197
742
2580
3684
4788
7385
34348
55604
86935
+
7913837
11436171
44121607
129572008
fibodiv
14
19
28
47
61
75
gapful
2580
147640
174680
298320
33445755
happy
19
28
4788
7913837
harmonic
28
Harshad
1104
2208
2580
298320
hex
19
61
hexagonal
28
hoax
34348
86935
hyperperfect
28
iban
14
47
742
1104
idoneal
28
inconsummate
75
31331
interprime
1537
3684
4788
junction
1104
2208
86935
355419
katadrome
61
75
742
Lucas
47
lucky
75
7909
355419
1084051
m-pointer
61
magnanimous
14
47
61
metadrome
14
19
28
47
modest
19
nialpdrome
61
75
742
nonagonal
75
oban
19
28
75
odious
14
19
28
47
61
1104
1537
2208
7647
7909
+
298320
355419
33445755
251133297
pancake
742
panconsummate
14
61
pandigital
19
75
742
perfect
28
pernicious
14
19
28
47
61
1104
1537
2208
7647
120284
298320
355419
Pierpont
19
plaindrome
14
19
28
47
4788
practical
28
1104
2208
2580
4788
174680
298320
694280
prime
19
47
61
197
1084051
Proth
1537
pseudoperfect
28
1104
2208
2580
3684
4788
147640
174680
183186
298320
694280
self
75
1537
3684
7385
7913837
semiprime
14
1537
7647
7909
34285
86935
129106
925993
7913837
44121607
Smith
4788
86935
sphenic
742
7385
31331
156146
strong prime
197
super-d
19
31331
34285
183186
355419
tau
2208
3684
4788
298320
triangular
28
trimorphic
75
truncatable prime
47
197
twin
19
61
197
uban
19
28
47
61
75
Ulam
28
47
197
34285
55604
93993
925993
unprimeable
2580
3684
7385
34348
62662
129106
156146
174680
183186
694280
untouchable
3684
156146
298320
upside-down
19
28
wasteful
28
75
742
1104
2208
2580
3684
4788
7385
7647
+
355419
694280
925993
7913837
weak prime
19
47
61
1084051
Zumkeller
28
1104
2208
2580
3684
4788